이번 시간에는 르벡적분의 성질을 보도록 한다.
만약에 Simple Function에 대해서 르벡적분을 한다면,

적분값이 단지 Measure의 합이므로, 르벡적분값이 또다른 Measure로서 작동할 수 있다는 말이 된다.
그러면, 일반적인 f에 대해서도, 르벡적분을 Measure로 쓸 수 있을까??
(Lebesgue Integral for Measure)

이 정리에 따르면, 일반적인 f에 대해서도 르벡적분을 Measure로서 쓸 수 있다!! (Countably Additive Set Function!)
(증명)
1.
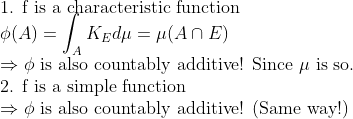
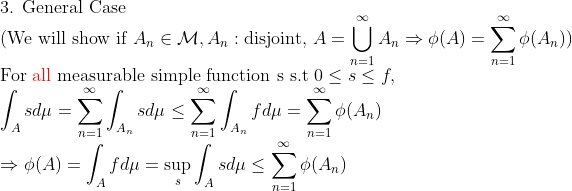
모든 measurable simple function에 대해서 성립해야 하므로, sup에 대해서도 (등호 붙어서) 부등식이 성립한다!
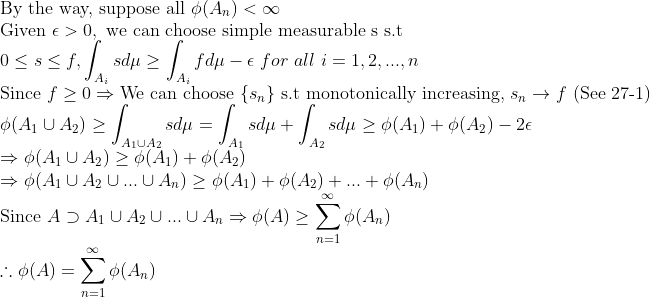
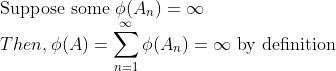
2. 르벡적분가능한 경우!
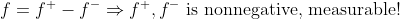
이므로, 위에서 나온 내용 그대로 적용하면 된다!
앞에서 다음 성질을 보았다!

그렇다면, 르벡적분이 Countably Additive 성질이 성립하므로
(Corollary)

즉, Measure가 0인 정도는 그냥 쿨하게 무시해도 된다는 것이다!
(Example)
우리가 앞에서 계속 예를 들었던 함수 하나를 가지고 오자!

즉, Countable개수 정도는 쿨하게 무시 해도 된다...
(심지어 거기에서 함숫값을 막 바꿔도 상관이 없다. -> 아마 대부분 쓰기 편하게 연속함수를 만드려고 할 것이다!)
-> 만일 lebesgue measure를 이용한다면, 저 적분값은 1이 될 것이다!
-> Uncountable이어도, measure가 0이면 상관없다! (Ex. Cantor set)
이러한 르벡적분의 성질을 정리해보자!
(Almost all)

여기서 나오는 Almost all의 개념은 다른 분야에서도 많이 쓰이므로 참고 바란다!
특히, 다음과 같은 성질을 얻을 수도 있다..

이를 고려하면 증명할 때 개념적으로 생각하기 편하다.
이번 챕터에선 르벡적분의 성질인 Almost all -> Measure zero는 고려하지 않아도 된다!
를 살펴보았다.
그런데, 이번 시간에 살펴본건 -> 적분구간(집합)에 대한 이야기 였고,
정작 기본적인 적분의 성질을 보지는 않았다... -> 예를 들어
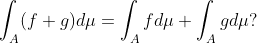
이런 간단한 이야기들은 하지도 않았다... (물론 Simple Function을 이용해서 증명할 수야 있겠지만, 위에서 본 바와 같이 simple function와 일반적인 function f 사이를 넘나들기 위해선 극한(limit)에 대한 논의가 필요하다.)
다음 시간엔 이러한 이야기들(사실, 극한에 대한 이야기들)을 해보자!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 28. 르벡적분과 리만적분 (Relation btw Lebesgue and Riemann) (0) | 2023.04.02 |
|---|---|
| (해석학) 27-3. 르벡적분과 극한 (Limit of Lebesgue Integral) (0) | 2023.04.01 |
| (해석학) 27-1. 드디어 르벡 적분의 정의(Definition of Lebesgue Integral) (0) | 2023.04.01 |
| (해석학) 26. 함수를 재보자! (Measurable Functions) (0) | 2023.03.31 |
| (해석학) 25-2. 측도의 정의 Extended.... (Definition of Measure 2) (0) | 2023.03.30 |



