지난 시간까진, 집합을 재어보았다면 이번 시간에는 함수를 재볼 것이다.
먼저, Measure가 정의된 Space에 대해서 생각해보자.
(Measure Space, Measurable Space)(측도 공간과 잴 수 있는 공간)

예를 들어서,
X가 자연수집합, sigma-ring을 X의 모든 부분집합, mu(A)를 A의 원소 개수라고 한다면 -> X는 잴 수 있는 공간!
그리고, 이 Measurable Space에서 정의된 함수에 대해서 Measurable Function을 정의하자.
(Measurable Function)(잴 수 있는 함수)

어떻게 생각하면 되냐면....
르벡적분 시작부분에서 다음 그림을 보았다!

르벡적분 부분에서, A의 길이(측도)는 결국에 저 가로로 길쭉한 직사각형의 가로 길이를 말하는 것이다!
-> A의 길이를 잴 수 있어야, 저 함수도 잴 수 있다고 할 수 있을 것이다!
(NOTE)
위 정의의 A에서

는 상관이 없다!!!
-> 앞 챕터에서 Open, Closed set에 mu*와 sigma-ring이 상관 없었던 것을 생각하자!
그리고, Trivial하게 다음 성질도 볼 수 있다!

다음으론, 잴 수 있는 함수의 함수열을 살펴보자... -> 극한을 보내도 Measurable이 보존이 되나?
(Limit of Measurable Functions)

즉, 극한을 태워 보내도 measurable의 성질은 보존된다! (물론, 그냥 lim이라면, 존재성을 증명해야 할 것이다!)
(증명)
sup, inf인 경우는 Trivial, limsup, liminf의 경우, 정의를 다시 떠올려보자!
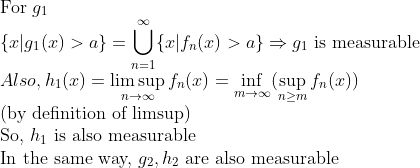
(Corollary)
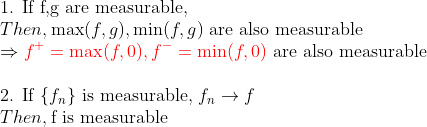
2번은 위에서 얘기한 내용이고, 1번은 사용할 일이 많은 함수들이니, Notation을 알아놓자!
이번엔, 덧셈과 곱셈에 대해서 Measurable이 보존이 되는지 살펴보자.
-> 덧셈과 곱셈도, 그냥 2개의 input을 받아서 1개의 output을 내주는 Function으로 생각할 수 있다...
이를 일반화해보면
(Measurable in 2D plane)

즉, 여기서 F가 단지 x+y 혹은 xy이면 위의 덧셈과 곱셈에 대해서 Measurable이 보존이 됨을 알 수 있다.
(증명)
Open set이 Base(open subset)의 Countable collection으로 표현될 수 있다는 것을 다시 한번 확인하자!

(NOTE)
1. 여기서 Nonmeasurable set, function (잴 수 없는...)에 대해서는 자세히 하지 않을 예정이다.
물론, Nonmeasurable의 경우가 많이 있지만 이걸 만들기가 상당히 어렵다..., 만드려면 억지로 고생해서 만들어야 한다.
-> 우리가 본 거 다 Measurable이라고 할 수 있을 정도!!!
그냥 예를 들어서, h(x)=f(g(x))에서, f가 measurable, g가 continuous인 경우, h가 nonmeasurable일 수도 있다....
2. Measurable Function을 정의할 때, Sigma-ring과 measure가 존재해야 한다고 했는데,
Measurable의 성질이 바뀌는 것은 사실 Measure에 따라서가 아닌, Sigma-Ring이 되나 안되나에 따라서 바뀌게 된다.
즉, Nonmeasurable인 경우, Sigma-Ring의 조건을 만족 못해서 생긴다. (그런 Measure가 없어서가 아니라)
-> 그래서 Measure와 독립적인 정의도 사실 가능하다...
(Borel-Measurable Functions)

다음 시간부터는 드디어 르벡 적분에 대해서 들어가볼 것이다!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 27-2. 르벡적분의 성질 (Almost all, Measure zero) (0) | 2023.04.01 |
|---|---|
| (해석학) 27-1. 드디어 르벡 적분의 정의(Definition of Lebesgue Integral) (0) | 2023.04.01 |
| (해석학) 25-2. 측도의 정의 Extended.... (Definition of Measure 2) (0) | 2023.03.30 |
| (해석학) 25-1. 르벡 적분의 시작 - 측도의 정의 (Definition of Measure) (0) | 2023.03.29 |
| (해석학) 24. 리만-스틸체스 적분의 문제점과 르벡적분의 등장(Lebesgue Integral) (0) | 2023.03.27 |



