(미적분학 참고링크)
(미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치환적분법): https://0418cshyun.tistory.com/37
(미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치환적분법)
다변수함수의 적분 챕터에서 계속 나오는 것이(예시로서든, 이론적으로서든) 적분을 우리가 아는 직교좌표계가 아닌, 극좌표계나 다른 좌표계(구면좌표계) 등에서 수행하는 것이다. 그만큼 중
0418cshyun.tistory.com
이번 챕터에서는 지난 챕터에 이어서, 다변수벡터함수의 적분을 "리만-스틸체스적분 처럼" 정의하려고 한다.
아직 남은 과제는
-> 순서대로 partition을 나누는 것과, 임의로 partition을 나누는 것이 동일한가??? 라는 것이다.
이를 위해서 우리의 목표는 다음과 같다.
적분할 때, basis를 마음대로 Change할 수 있는가???(미적분학에서 좌표계 변환으로 불린 바로 그것!)
만일 이게 보장되면
임의의 basis에서 Partition을 나눈 것을 ->
Standard basis로 Partition을 옮겨서 생각하면 간단하게 k-cell의 Partition으로 표현 가능할 것이다!
예를 들어서, 반지름이 1인 원 내부에서 적분한다고 하자.
그럼, Partition을 나눌 때, 다음과 같이 생각할 수 있다.
1. 직교좌표계를 이용한다 -> 직사각형
-> 아래 첫번째 그림

2. 극좌표계를 이용한다 -> 아치꼴
-> 아래 두번째 그림

만일, 첫번째의 경우를 이용한 결과(임의로 자른 Partition이라고 생각하자!)와 두번째의 경우(우리가 원하는 basis -> k-cell)의 결과가 동일하다면 k-cell로 옮겨서 적분의 정의를 생각하면 되므로, 임의의 Partition으로 한다고 해도 전혀 문제 될 것이 없을 것이다!

이를 설명하기 위해서, 다음 개념들을 설명하자...
(Primitive Mapping)

즉, 한 축에서만 움직이는 Mapping을 Primitive Mapping이라고 한다.
G의 Jacobian은 다음과 같이 쓸 수도 있다. (단, g가 미분가능하면)

그러므로 이 Primitive Mapping G의 역함수(역행렬)존재조건은

이 된다.
(Flip)(In linear algebra)
basis의 순서를 "한번"만 바꾸는 mapping을 Flip이라고 한다.
즉, 다음 mapping은 flip이다.

그럼, 다음 성질을 증명해보자.
(Locally Primitive Mapping)

즉, F가 특정조건을 만족하면(결국 역함수정리와 동일하다),
F는 Locally, 각 basis로 쪼개질 수 있다(primitive mapping으로)는 것을 말한다.
(증명)
증명을 시작하기 전에 Notation 하나만 보고 가자.
(Projection)
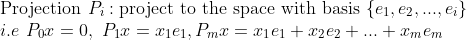
증명을 시작해보자!
주어진 F에서 하나하나씩 차원을 낮춰나가자. 일단 m=1인 경우부터 살펴보자! 위의 가정에 의해서 다음과 같은 전개를 한다.
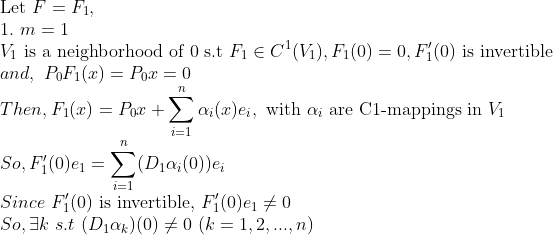
그러면, 여기서 Primitive Mapping G를 만들어보자!
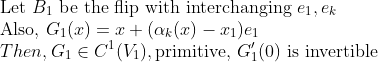
이 G에 대해서 Inverse Function Theorem을 이용하자!

그럼 이제 차원을 낮춰보자!(e_1에 대한 것을 날린다!)
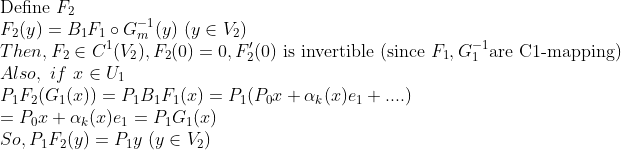
자, 그럼 다시 처음으로 돌아가서 m=2,3,...인 경우도 살펴보자! (위에 내용 반복!)
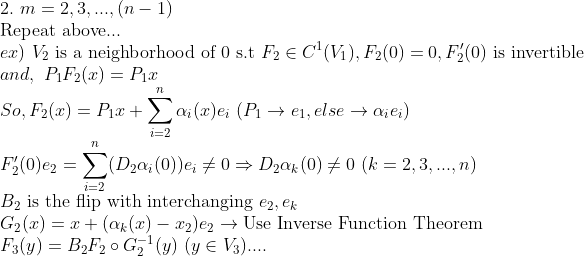
이를 반복하면 결국
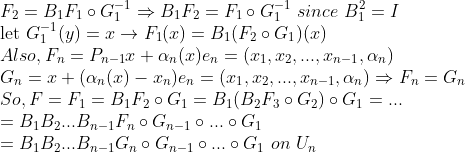
이므로 증명이 완료된다.
위 성질을 이용하면, 임의의 mapping을 각 축의 mapping(Primitive mapping)의 composition으로 나타낼 수 있다는 것을 증명할 수 있다.
또한, 다음 성질을 살펴보자.
(Partition of Unity mapping)

(증명)
일단 s개의 open set을 잡아서 finite open cover를 만들어보자.
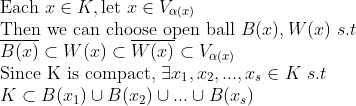
그리고 다음과 같은 phi함수를 만들어보자. (continuous)
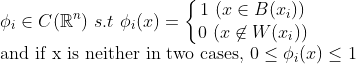
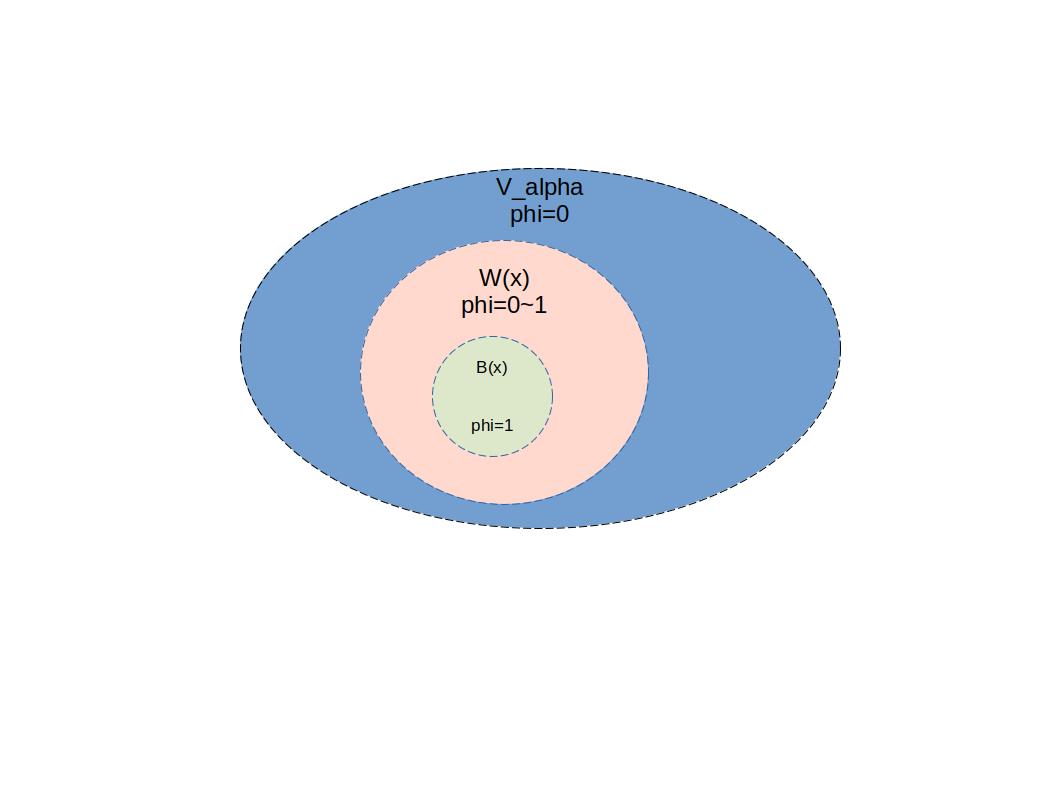
이러한 상황에서, psi함수를 만들어보자!
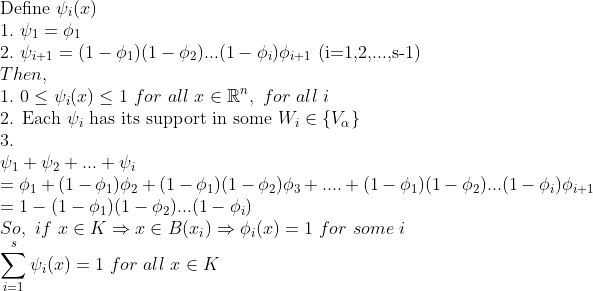
그러므로, 3가지 조건을 모두 만족하는 psi함수를 만들었다.
(Corollary)

즉, 연속성이 계속 보장된다!
그러면, 드디어 미적분학에서 다루었었고, 우리의 목표인 적분에서의 Change of Basis(Coordinate)를 증명할 수 있다!
(Change of Basis(Coordinates))

1. 1대1대응 T로 basis 변환이 가능하고,
사실, T의 inverse가 locally continuous이고(by 역함수정리), support가 compact였으므로, support를 Inverse 태워 보낸 것도, compact이다. 그러므로, T를 보내기 전, 후 둘 다 Compact set에서 정의되므로, 적분가능성은 보장된다!
2. 식을 보면, 차이가 (det J_T) 만큼 난다는 것을 알 수 있다.
f=1이라면 그냥 Volume일 것이므로, (det J_T(x)) 는 x에서의 T로 인한 Volume 변화량이라는 것을 알 수 있다!!
또한, 별거 아니고, 그냥 치환적분법으로도 볼 수 있다!
(증명)
일단, Trivial한 다음 두 개의 Mapping을 생각해보자.

1번의 경우, primitive mapping이면 어차피 1변수로 생각할 수 있겠고,
2번의 경우 Flip이라면, 앞에서 본것과 같이, 적분순서는 어차피 상관없게 되므로, Change of basis를 만족한다.
그러면, 적어도 저 위 성질을 만족하는 mapping은 두 가지가 있다. 이를 각각 P, Q라고 해보자. 그럼, 이를 합성한 mapping의 경우
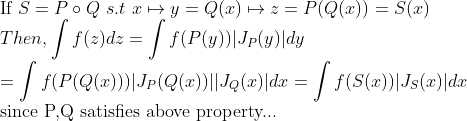
Change of basis를 또한 만족한다.
자 그렇다면, 다시 우리 문제로 돌아와서 T에 대해서 생각해보자... T가 locally primitive한 것을 이용하면
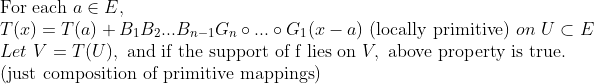
만약에 support가 V 안에 놓인다면, T는 primitive mapping의 composition일 뿐이므로, Change of basis를 만족할 것이다.
그러면 남은 것은, support가 V안에 놓이냐는 것인데, 이는 우리가 했던 Partition of Unity를 이용하면 된다.
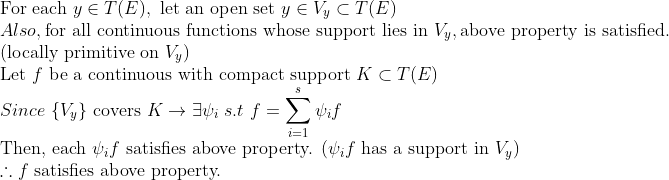
즉, 저 각각의 psi*f의 support는 각 cover 안으로 쏙 들어가버려서 change of basis를 만족하고, K 전역에서 성립하므로, K 전체로 성질이 확장될 수 있다!
자, 그럼 여기까지의 내용을 정리하자면
Partition를 임의로 잡아버리면 -> Change of basis를 이용해서 k-cell에서 생각하는 것으로 넘길 수 있고 -> k-cell에서는 적분 순서도 문제가 되지 않는다!
그러므로, 결국 다변수벡터함수의 적분을 마치 "리만"적분처럼 정의를 한 것이나 다름 없다.
다음시간부터는 미분형식에 대한 내용으로 넘어가본다.



