이번챕터에선 지난번에 이어서 미분형식에 관한 이야기를 계속 해보자.
1. 미분형식 w=0의 의미 확장
미분형식 w는 어떤 Parameter Domain을 받는 함수라고 생각했어서
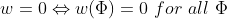
이런 성질을 만족했었다.
그런데 이를 확장하면 다음과 같은 성질을 얻을 수 있다. (여기서 모든 미분형식은 Standard Presentation!)
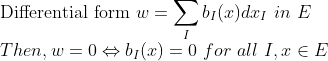
(증명)
귀류법으로 증명하자!
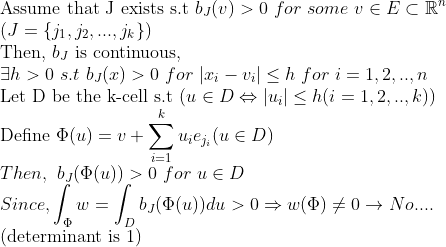
만일 b_I>0인 것이 존재하면, 위의 Phi함수로 적분하면, 값이 항상 0보다 크게 나오므로, w=0이라는 것에 모순이다....
그러므로, 모든 I에서 b_I=0
그러므로, 미분형식은 저런 형태의 sum으로 나타내는 것이 어떻게 보면 당연하다고 할 수 있다.
2. 미분형식의 곱
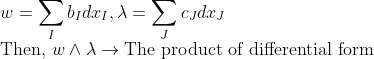
사실 여기서 문제 될 것은 dx_I 부분이고, 나머지는 그냥 곱해주면 된다.
일단, b,c 함수는 제껴두고, dx_I, dx_J에 대해서 살펴보면
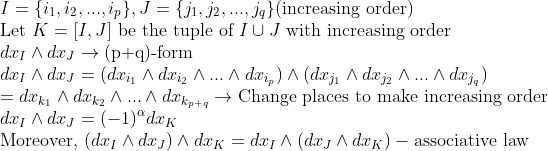
즉, "순서"만 잘 고려해주면 된다!
그래서 Product of Differential Form은 다음과 같이 정의한다.
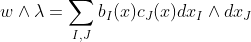
그러면 다음과 같은 성질을 얻을 수 있다!
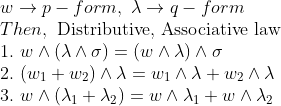
정의가 함수부분은 곱으로, dx부분은 그냥 순서만 맞추면 되므로, 위 성질이 바로 나오게 된다.
3. 0-form
용어가 헷갈릴 수도 있어서 잠시 적어보자면, 0-form이라면... -> dx부분이 없다! -> 그냥 함수이다!
또한, 미분형식의 미분도 정의할 수 있다!
(Differentiation of Differential Form)
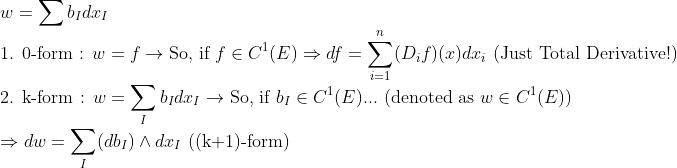
1. 일단 미분가능해야 하므로, 각각의 b_I가 C1-mapping이어야 함은 자명하다!
2. 특히, 0-form의 미분의 경우 "전미분"으로 써져야 한다!! -> 미적분학에서 궁금했던 Notation 해결!
2-1. 그러므로, 저 미분할 때 붙는 d를 함수를 함수로 mapping 시키는 -> 미분연산자(Differential Operator)로 볼 수 있다!
(Linear Operator(선형연산자) -> Domain과 Range가 서로 같은 Linear Mapping)
(Differential Operator(미분연산자) -> Domain(함수)과 Range(함수)가 서로 같다!)
3. 특히 "모든" 방향에 대해서 미분해야 한다는 것에 초점을 맞추자!
왜 이런식으로 정의했는지 예시로 알아보자.
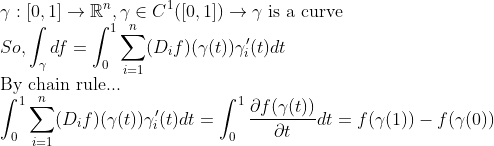
즉, "전미분"처럼 사용할 수 있다!
이를 이용한 성질을 보면
(Property of Differentiation of Differential Form)
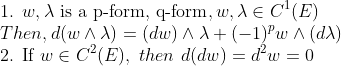
(증명)
1. 어차피 sum부분은 따로 생각할 수 있으므로, 미분형식이 그냥 1개의 항만 가지고 있다고 생각하자. -> 순서만 유의하면 된다.
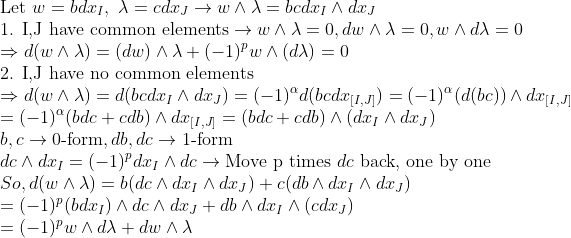
dc dx_1에서 맨 앞에 있는 것을 하나씩 맨 뒤로 보내면 된다!
2.
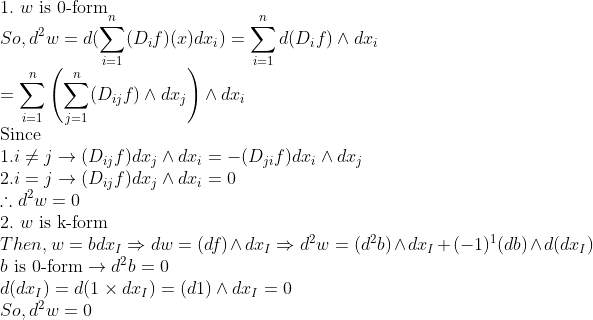
여기까지 미분형식을 미분하는 방법에 대해서 보았다.
미적분학에서 미분형식에 대한 언급을 살짝한 것에 대한 대답은 되었을지 모르겠지만, 아직까지는 미분형식을 미분하고 이러는게 어디에 써먹을 지 아직 감이 안 올 수도 있을 것이다...
그런데, 결국엔 미적분학에서 보았던 다변수벡터함수의 적분 성질들 (예를 들어서, 스토크스 정리나, 발산 정리, 선적분의 기본정리 등....)을 조금 더 일반화해서 정리하는데 꼭 필요한 내용들이 된다.
다음시간엔 미분형식과 Change of Basis를 결합해서 생각해보도록 한다.



