이번 챕터부터 다변수벡터함수(MIMO)의 적분에 대해서 들어가려고 한다.
이해를 돕기 위해서 일변수함수(SISO)의 적분(리만-스틸체스적분)과 비교해보자...
일단, 먼저 적분을 위해서는 적분 구간(닫힌 구간)이 필요했었고, 이를 Partitiion으로 잘게 쪼개는 작업이 필요했었다.
1. SIMO(일변수벡터함수)
-> 이 경우엔, 적분 구간은 동일하게 잡으면 될 것이다.(어차피 하나의 변수이므로...)
-> 적분 값이 벡터인데, 사실 이는 함수의 각 성분마다 적분하면 될 것이다.
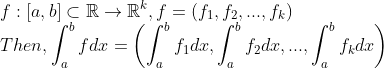
2. MISO(다변수함수)
-> 이 경우엔, 적분구간을 어떻게 잡아야 할까????
-> 가장 심플한 적분구간은 아마 K-cell이 될 것이다....
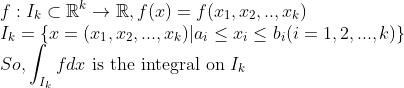
-> 물론, 저 k-cell에서 Partition을 잡는 방법이나, x_i들의 순서를 고려해주어야 할 것이다. 이는 잠시후에 볼 것이다.
3. MIMO(다변수벡터함수)
-> 이 경우엔, SIMO와 MISO의 경우를 합해서 생각하면 될 것이다...
-> 문제가 되는 경우는 MISO이므로, 이 경우만 잘 정의되면, MIMO의 경우로 충분히 확장할 수 있을 것이다!
결국 위 내용은 MISO를 잘 정의하면 된다는 것일 뿐이다.
자, 그러면 이제부터 MISO의 적분을 한번 잘 정의해보자. -> MISO에서 가장 심플한 적분구간인 k-cell의 경우로 다시 돌아가면
1. Partition을 잡는 방법? -> 일단 가장 심플하게
k-cell이 공간에서 마치 직사각형, 직육면체처럼 생긴 것은 이미 알고 있는 내용인데, 이를 "임의로" Partition으로 나누는 건 Multi-Dimension에서는 규칙을 정하기 어려워보인다... (Refinement 정의하기도 약간 애매해지고....) -> 여기에 대해선 나중에 생각하자
그러므로, 이번에도 가장 심플하게, 각 변수 하나하나씩 독립적으로 생각한다...
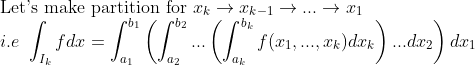
이런 식으로 접근해보면...
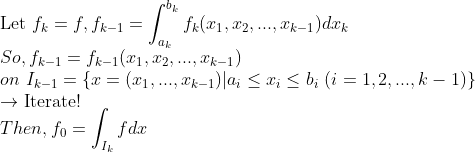
이 때 f가 continuous이면, 각각의 f_k가 모두 Uniformly continuous가 되므로, 적분가능성이 계속 보장된다.
(사실, 우리가 앞에서 f가 적분가능하면 -> 적분값이 동일한(2-norm sense로의 차이가 -> 0이 되는) 연속함수를 구할 수 있었다!
-> 그러므로, (f가 적분가능하다 -> continuous)라고 생각해도 무방하다!)
일단, 가장 심플하게 k-cell에서 적분을 정의해보았다.
2. 적분순서는?
위에선 그냥 심플하게 x_k -> ..... -> x_1 순서대로 적분을 해봤는데, 이 적분 순서를 바꾸어도 상관이 없는 것일까?
-> 연속함수면 상관이 없다!!!
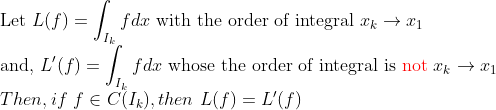
(증명)
Stone-Weierstrass Thm을 이용해보자!
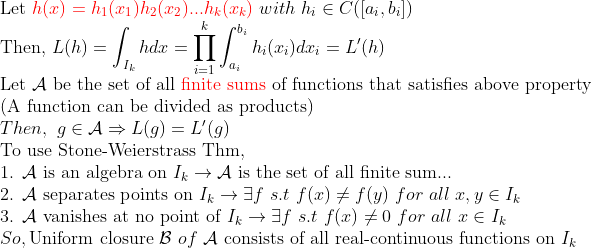

즉, 저렇게 곱으로 쪼개지는 함수와 연속함수가 Dense관계에 있다는 것을 알 수 있다. 이를 이용하면...
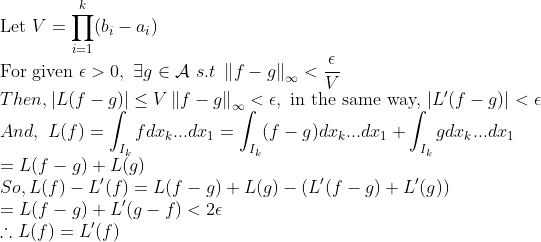
이제부턴 k-cell말고, 조금 더 복잡한 적분구간에 대해서 생각해보자..
어차피 우린 계속 닫힌 구간(k-cell이던지, 아니면 [a,b]이던지...)에 대해서 적분하고 있다. 그러므로, 이 외의 구간에 대해선 상관할 게 없다.
게다가, f(x)=0이면, 어차피 적분값이 0이므로, 여기도 적분할 이유가 없다. 여기에 관련된 Support라는 용어를 보자.
(Support)
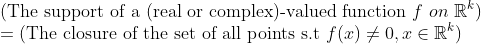
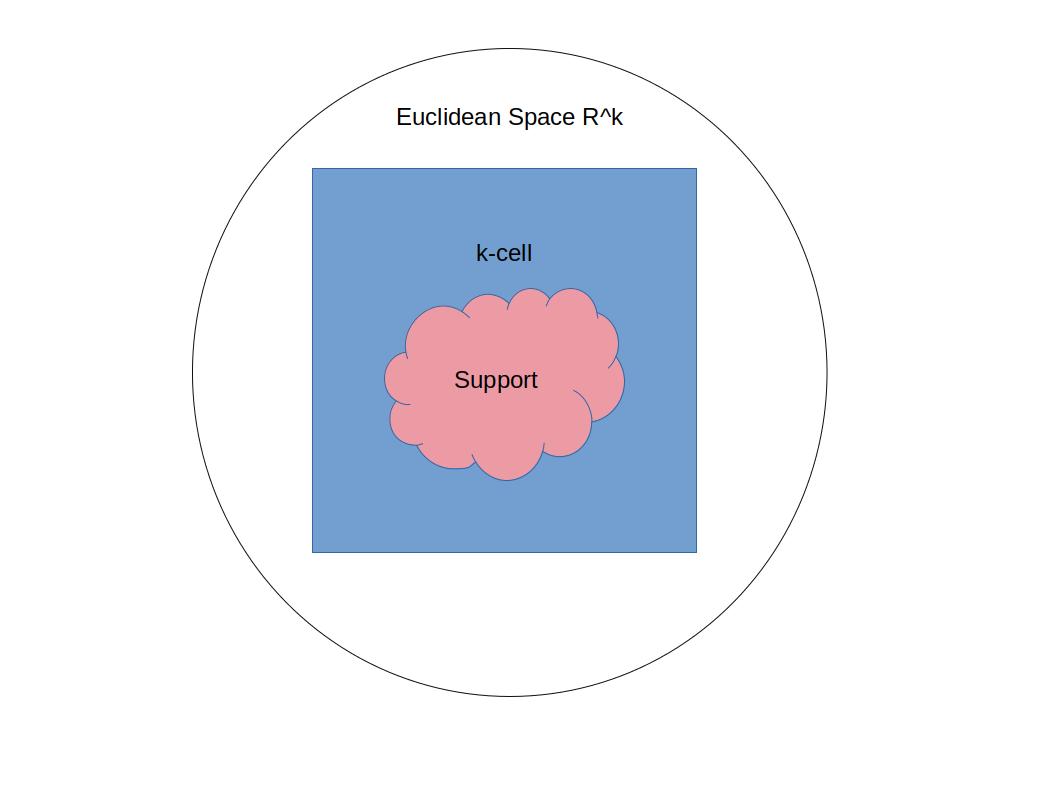
이를 이용하면 닫힌 구간 말고도 다양한 적분 구간에 대해서 적분을 정의할 수 있다. 예를 들어서, 위의 그림과 같은 상황일 때,
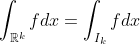
즉,
1. "더 넓은 구간"을 적분할 때, k-cell로 줄여서 생각하면 된다!
2. "임의의 적분구간(Support)"에서 적분할 때, k-cell로 늘려서 생각하면 된다! -> Support 밖에서의 f는 f=0으로 확장!
여기까지, 기초적인 다변수벡터함수의 적분(사실 MISO이긴 하지만, 별로 차이는 없다.)을 살펴보았다.
일단, Partition을 "임의로" 잡는 것은 나중으로 하고, 순서대로 적분으로 "일단" 정의하고.
(K-CELL -> 결국 임의의 적분구간)에서 적분순서는 상관이 없었다!
그럼, 남은 건 임의로 Partition을 잡는것과 위처럼 순서대로 적분하는게 차이가 없다는 것인데, 이를 어떻게 보일까?
다음 챕터에서 확인하자.



