이번 챕터에서는 미적분학에서 살짝 언급이 되었던 미분형식에 관한 내용으로 들어갈 것이다.
미분형식에 대한 내용을 설명하기 전, Parameter Domain에 대해서 살펴보자.
예를 들어서, "임의의" 적분구간 Y에서 적분한다고 하자.
앞 챕터에서 예를 들었지만, 만일 Y가 반지름이 1인 단위 원이라고 한다면
-> 1. 직교좌표계의 경우 -> x,y의 범위를 정할 수야 있는데, 범위 정하기가 뒤에 나올 극좌표계보다 까다롭다...
-> 2. 극좌표계인 경우 -> r, theta의 범위를 k-cell로 정할수가 있다! (0<r<1, -pi<theta<pi) -> 그냥 직사각형...
2번 방법이 쉽기 때문에, 우리는 2번 방법을 택할 것이다. 그러면 적분구간의 변화는 다음과 같다.

즉, 앞에서 보았던 Change of Basis에 따르면...

이 때는 적분 범위가 전역이었지만, 여기선 적분범위가 저 직사각형과 원으로 제한된다. -> Support!
즉, 다음과 같다.

이 때의 X를 Parameter Domain이라고 한다. ((Parameter -> r,theta)의 Domain!)
정리하자면
원에서 적분을 하고 싶은데, 그냥 하기는 어려우니, Change of Basis를 이용한다.
그러면, 적분구간도 원이 아니라 T에 inverse를 태운 구간으로 바뀐다. 이 구간을 Parameter Domain이라고 한다!
(k-surface, Parameter Domain)

즉, 위의 예에선 T가 2-surface가 된다. (k=2)

k-surface에 대해서 이해가 잘 안된다면, Curve를 생각하면 된다.
Curve는

이었던걸 생각해보면, Curve는 1-surface이다!
이제 미분형식에 대해서 알아보자!
(Differential Form)(미분형식)

(1)은 미분형식을 그냥 저렇게 쓴다는 것이고 (둘이 동일한 표현!)
(2)는 미분형식의 의미인데,
이렇게 보면 되게 어려워 보이지만 미분형식 w를 k-surface(Phi)를 받아서 적분값을 뱉는 함수라고 생각하자!
즉, 미분형식 w는

인 함수이다.
아직도 이해가 안된다면 맨 위의 예시를 생각해보자!

여기서 f가 사라지고 (f=1), Y가 Phi로, X가 Parameter Domain D로 바뀌었을 뿐이다!
이해를 돕기 위해서 예시를 몇가지 들어보자.
1. Curve

3차원으로 mapping되는 curve에 대해서 저 미분형식에 대해 적분을 해보자!
3차원일 때는, 흔히 x,y,z로 많이 쓰긴 하지만, 여기선 혼동을 줄이기 위해서 x_1,x_2,x_3으로 바꾸어 썼다.
2. Sphere
구의 부피를 구해보자!
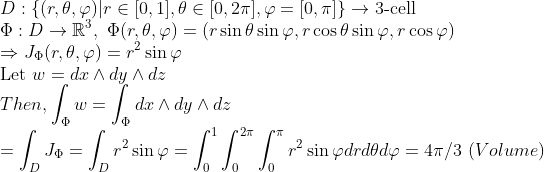
여기까지 보면, 미분형식을 단지
-> Basis를 Phi로 옮겨 간 "후"의 적분이라고 생각하면 된다!(단, 의미만!!! -> 값은 부호 등을 따져야 하므로 다를 수도 있음)
(저 Wedge를 생각할 때 -> 옮겨간 후의 dxdydz in Phi -> 결국 구의 부피!)
미분형식의 몇 가지 성질을 살펴보고 가자!
(Properties of Differential Form)
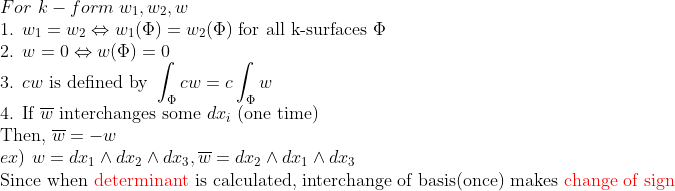
특히 여기서 주목할 것은 4번인데, 미분형식을 계산할 때, determinant를 가지고 있으므로, basis 자리를 서로 바꾸면, determinant 성질에 의해서 부호가 뒤바뀐다...(물론 자리를 서로 1번 바꾸면 -> 부호 1번 바뀜)
그러므로 다음과 같은 성질을 만족한다.
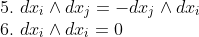
특히, 4,5,6번을 주목하기 바란다!
우리가 미분형식을 정의할 때는, 저 basis의 순서를 따지지는 않았지만, 위에서 4,5,6번 성질을 보면서, 기왕이면 basis 순서를 정리하는게 생각하기도 좋고, 식 정리하기도 편할 것이다...
그러므로 basis의 순서를 일부러 정렬해서 생각한 것이 Basic k-form이다.
(Basic k-form)

그러면, basic k-form으로 변환하면, 더하는 원소 각각에 대해서 1이나 -1을 곱한거 만큼이나 차이가 날 것이다.
예를 들어서

일단, 여기까지 Differential Form(미분형식)의 의미와 간단한 성질 몇가지만 보았다.
이제 이 미분형식의 성질을 더 본 후, 다양한 적분에 대한 내용들로 들어갈 것이다.



