(해석학 참고링크)
(해석학) 19-2. 다변수벡터함수의 적분을 정의하자! (Change of Coordinates(Basis)): https://0418cshyun.tistory.com/92
(해석학) 23-1. 벡터장과 미분형식, 그리고 면적분 (Vector Field, Differential Form, and Surface Integral): https://0418cshyun.tistory.com/101
(해석학) 23-1. 벡터장과 미분형식, 그리고 면적분 (Vector Field, Differential Form, and Surface Integral)
(미적분학 참고링크) (미적분학) 15-3. 더더, 선적분 (Fundamental Theorem in Line Integral, Potential Function): https://0418cshyun.tistory.com/34 (미적분학) 16-1. 선적분과 비슷한 듯... 면적분 (Surface Integral): https://0418cs
0418cshyun.tistory.com
(해석학) 19-2. 다변수벡터함수의 적분을 정의하자! (Change of Coordinates(Basis))
(미적분학 참고링크) (미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치환적분법): https://0418cshyun.tistory.com/37 (미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치
0418cshyun.tistory.com
다변수함수의 적분 챕터에서 계속 나오는 것이(예시로서든, 이론적으로서든) 적분을 우리가 아는 직교좌표계가 아닌, 극좌표계나 다른 좌표계(구면좌표계) 등에서 수행하는 것이다. 그만큼 중요한 개념이고, 특히 물리학분야에서 회전(토크) 개념이 나오기 시작하면 안 쓸 수가 없다...
지금까지 나왔던 좌표계 변환하여 적분하는 것을 정리해보면 다음과 같다.
- 1. 선적분


벡터장 F를 곡선 s에서 (내적으로) 적분하는 것으로, 곡선 위로의 좌표계 변환을 하고 있다. -> 적분결과는 실수(1차원)

일변수함수 f를 곡선 s에서 적분하는 것으로, 곡선 위로의 좌표계 변환을 하고 있다. -> 적분결과는 실수(1차원)

(여기서 15-2와 비교해보자!!)
15-2는 극좌표계 상황에서 length를 구하려니 length를 구하는 방법 자체가 바뀌었고,
여기서는 직교좌표계 안에서 극좌표계의 length를 구하려고 하고 있다.
- 2. 면적분


벡터장 F를 곡면 S에서 적분한다. (내적을 통해서) -> 첫번째 예시는 구면(r=1) 위에서 적분, 적분결과는 1차원 실수

일변수함수 f를 곡면 S에서 적분한다. 적분결과는 1차원 실수
자, 여기서 좌표계 변환에 관한 이야기를 해보자.
먼저 좌표계 변환은, 선적분예시 1,2에서 나온 것처럼 기존에 있던 좌표계(직교좌표계)에서 다른 좌표계(곡선 위의 좌표계)로 변환하는 과정을 말하고, 나머지 예시에서는 그냥 곡선과 곡면을 극좌표계에서 잡아서 극좌표계에서 계산을 한 것 뿐이다.
선적분의 1번예시의 좌표계 변환은 다음과 같은 변환에 의해 일어난다.
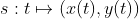
xy좌표계 위에서의 적분과 곡선 위에서의 적분을 비교하면 다음과 같다.

이미 gradient와 jacobian의 개념에서 알고 있듯이, 위의 차이는

에서 나오는 것을 알고 있다. (물론 방향에 대한 문제는 있지만, 방향을 무시한다면)
이를 다음과 같이 해석할 수도 있다.
xy좌표계에서 t가 dt만큼 변하면, 곡선에서 곡선벡터 s가 s'(t)dt만큼 변한다. |
이를 곡면에 적용한다면, xyz좌표계에서 u,v가 du, dv만큼 변하면, 곡면에서 면적벡터 S가 |N|dudv만큼 변한다. |
지금은 곡선과 곡면에 대해서만 이야기했지만, 일반적으로는 Multiple Integral에서 다음처럼 생각할수도 있다.

n차원 좌표계에서 x_1,...,x_n가 dx_1,.., dx_n만큼 변하면, T로 움직여진 좌표계(m차원)에서 u_1,...,u_m가 (Jacobian)* du_1,...,du_m만큼 변한다.
저 x와 u가 각각 orthogonal(수직) basis라고 하면 (즉, 3차원에서 x,y,z축이 수직한거라고 생각하자.)
dx_1dx_2...dx_n와 du_1,....du_m은 각 좌표계에서의 미소 부피라고 할 수 있다. (즉, 3차원에서 dxdydz=dV는 미소부피(직육면체))
이 미소부피의 크기는 저 Jacobian의 크기에 의해서 변화한다. (부피는 방향 정의하기 애매하므로 크기만 생각하자)
(Relation btw Jacobian and Determinant in Linear mapping)
여기서 저 Jacobian의 크기에 대해서 생각해보자.
만일 변환 T가 다음과 같다면,

즉, jacobian의 크기는 그냥 (변환의 determinant)의 크기로 정의할 수 있다.
사실, 모든 한 점에서 모든 변환은 아주 작은 범위 내에서 선형(Locally Linear)이므로 위의 내용을 사용할 수 있다. (해석학 참고!)
그러므로 위에서 미소부피의 변화는 determinant의 크기에 의해 변화되고, 정리하면 다음과 같이 쓸 수 있다.

특히, 다중 적분에서 du와 dx를, 이런 식의 관계를 이용해 바꿔치기가 가능하다. (치환적분)
(Note) 설명이 약간 부자연스러울 수 있어서 추가....
(u가 m차원에서 n차원으로 바뀌었다! -> 곡면에서의 예를 들면 n=2, m=3이었는데 사실 곡면의 z축이 항상 0이므로, m=2라고 생각할 수 있다... 또한, 곡면에서 |N|은 생각해보면 결국 곡면으로 변환하는 T(선형이라 T'와 동일)의 determinant와 동일하다.)


예시를 하나 들어보자.
(구의 부피 구하기)
반지름이 1이고 중심이 (0,0,0)인 구의 부피를 구해보자.
1. xyz 좌표계의 경우...
구를 xyz좌표계에서 구간을 잡아서 정의하면 다음과 같다.
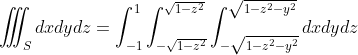
이를 적분하면

구간 잡기도 헷갈리고 계산 실수나기 딱 좋은 꼴이다...

2. 구면좌표계의 경우...

저 determinant만 구하면, 다 decoupling이 되기 때문에 단독으로 적분하므로 아주 쉽게 부피를 구할 수 있다.

또 다른 예시를 들어보자.
(정규분포)
통계시간에 아주 많이 보는 정규분포곡선의 식은 다음과 같다.
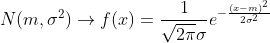
왜 이런 식이 나왔는지는 일단 둘째치고, 평균이 0, 분산이 1인 경우(Normalize)일 때

을 만족해야 할 것이다. (확률을 다 더하면 1이어야 하므로...)
이를 증명해보자!
일단, 이 적분이 수렴한다고 가정하고 들어가자(수렴성 확인은 다른 문제...)
그렇다면, 다음과 같은 식이 성립하는 것을 보이면 된다.

(증명)
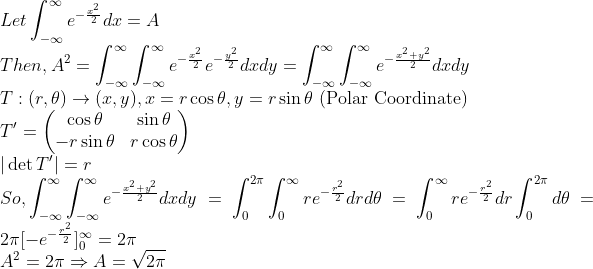
일변수함수 적분을 다중적분으로 바꿔서 (동일한 것을 또 곱해서) 극좌표계로 변환하면 풀린다!
(NOTE) 잘 쓰는 다중적분 치환적분법 공식 -> 치환할 때 determinant의 크기를 정리해놓음!
1. 직교좌표계 <-> 극좌표계

2. 직교좌표계 <-> 원통형 좌표계(Cylinder)

3. 직교좌표계 <-> 구면좌표계

여기까지, 좌표계 변환과 다변수함수에 대한 치환적분에 대해서 알아보았다. 특히, 좌표계 변환을 통해서 다중적분이 아주 용이해지고, 손대지 못하던 적분까지 할 수 있었다.
이렇게 좌표계 변환(치환적분)은 적분에서 아주 중요한 역할을 하므로, 꼭 알아두자!
다음 챕터부터는 벡터 미적분의 성질에 들어가는
divergence와 curl, 그리고 이를 이용한 divergence 정리나 stokes 정리에 대해서 알아보자. 이게 마지막 개념들이다. 다 왔다!!



