이번 챕터에서는 물리학에서 꽤나 많이 쓰이는 발산(Divergence)과 회전(Rotation)에 대해서 알아볼 것이다.
17-1에서는 2D에서, 17-2에서는 3D에서 살펴볼 것이다.
일단, 2D에서
(Divergence(발산))
다음과 같은 벡터장 F가 주어졌을 때, Divergence는 다음과 같다.

(Note) 미분 operator del을 이용한 표현에서, 아래 표현들을 헷갈리지 말자!

(벡터장이라 gradient 표현을 확장했다. -> F가 R^n -> R^1 이면, del F는 우리가 아는 gradient 표현일 것이다.)
(Rotation(회전도))
위와 같은 벡터장 F가 주어졌을 때, Rotation은 다음과 같다.

3D에서 보겠지만, Rotation은 Curl을 2차원에서 본 것이다.
저 발산과 회전도가 어떤 의미인지 확인해보자.
1. Divergence의 의미
각각의

는 벡터장 F의 각 축으로의 속도 벡터라고 할 수 있다.
그렇다면, 이를 다 합치면, 벡터장이 원점으로부터 나가는 정도를 표현하는 것이라고 할 수 있다.
보다 정확하게는 벡터장에 의한 부피 변화량으로 생각할 수 있다.
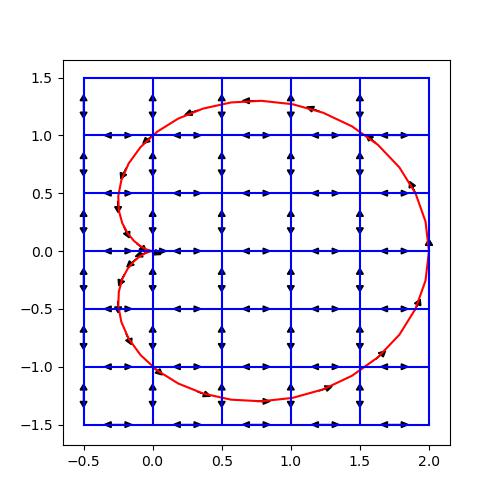
잘 이해가 안 가는 사람들을 위해서, 예시를 들어보자. (15-3 선적분 파트 예시)
이 경우에 원 C에서 벡터장 밖이나 안으로 퍼져나가지 않는다.


다음 경우에는 벡터장이 원점으로부터 퍼져나가게 된다.


이 경우에는 divergence가 0이 아니게 된다. (원점으로부터 퍼져나가므로)
또한, divergence가 부피 변화량이라는 이야기는 다음 증명으로 보일 수 있다.
(증명) (3D인 경우로 증명함)
시간이 t=0일 때 어떤 부피(면적) V를 잡자. 그러면, V 내부에 있는 점은 벡터장 F에 의해서 시간이 t일 때, 부피가 V(t)으로 바뀔 것이다. 이 때, 이를 기술하는 mapping(T_t)을 다음과 같이 잡자.

여기서 평균값 정리를 이용하면,

즉, 한 점에서의 divergence는 부피의 변화량을 이야기한다.
(Note) Trace in Matrix

또한, 중간에 다음과 같은 Lemma를 이용하였다.
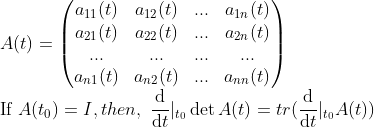
(증명)

(sigma를 잡을 때, 대각성분만 살아남는다)
2. Rotation의 의미
Divergence의 예시를 그대로 들고 오자.
그러면,


딱 보아도 회전하는 벡터장에서는 rotation이 0이 아니다.
그러나 다음 예에선 회전도가 0인 것을 확인할 수 있다.


이렇듯, 회전도는 벡터장이 회전(벡터장을 따라가면 다시 원 위치로 오는지...)하는지를 보여준다.
일단 개념은 알았고, 이제 중요한 발산정리(Divergence Theorem)과 그린정리(Green's Theorem)에 대해서 알아보자!
1. 발산정리(Divergence Theorem)(1차원<->2차원)

즉, boundary(경계면)을 따라서 수직방향으로의 적분은, 영역 내부 전체에서의 divergence와 동일하다는 내용이다.
여기서는 일단 영역 D를 bounded, closed(compact)라고 하고, 또한, boundary(경계면)은 이 D의 경계를 이야기하고, 방향(n)은 D에서 밖으로 나가는 방향으로 정의하자.
예를 들어서,


사실 이런식으로 써놓았지만, 물리적으로는 다음과 같이 생각하면 된다.
(내부의 divergence의 변화는 경계면에서의 흐름(flux)만 확인하면 된다!)
일종의 에너지 보존처럼 생각할 수 있다는 것이다! -> 경계면에서의 물리량의 흐름만 체크해주면 된다!
(증명)
먼저, 간단한 경우(직사각형)의 증명을 살펴보자.


직사각형인 경우에는 증명이 완료 되었고, 이와 비슷한 방법으로 직사각형에서 한 쪽 boundary가 곡선으로 표현되는 영역의 경우도 증명할 수 있다. 일반적인 영역에서는 주어진 영역을 직사각형으로 잘게 쪼개서, 또한, 직사각형으로 안 나눠지는 곳은 한 쪽 boundary만 곡선으로 나타낼 수 있을 것이다. 이 때, 영역 내부에서 각 조각의 divergence는 서로 반대 방향으로 상쇄되므로, 모든 조각들의 적분값의 합은, 전체 영역의 divergence의 적분값과 동일하다.


그러므로, 직사각형에서 발산정리를 증명하였으므로, 일반적인 영역에서도 발산정리가 성립한다.
이는 3차원이나 고차원으로 확장해도 똑같이 성립한다!
2. 그린정리(Green's Theorem) (1차원 <-> 2차원)

즉, 영역 경계를 따라서 (곡선방향으로) 적분한 결과는 영역 전체에서의 rotation과 동일하다는 것이다.
증명을 확인하면, 이 정리가 무엇을 뜻하는지 바로 알 수 있다.
(증명)
증명 flow는 위의 발산정리와 동일하다.
1. 직사각형에서 증명 -> 2. 일반적인 모양에서의 증명
먼저, 직사각형에서 증명해보자.


발산정리와 같은 방법으로 일반적인 모양의 영역에서 생각해보면, 일반적인 모양에서도 성립함을 알 수 있다.

발산정리와 그린정리를 이용하면, 면적을 얻을 수도 있다.
1. 발산정리를 이용한 넓이 계산

2. 그린정리를 이용한 넓이 계산

주어진 곡선(경계면)에 따라서 둘 중 어떤 것을 이용하는게 편할 때가 다르므로, 그때그때 편한거 이용하면 된다.
지금까지 2차원 평면에서 divergence와 rotation에 대해서 알아보았다.
여기선 간단한 응용만 보았지만, 물리학에서 특히 맥스웰 방정식 등에서 정리들이 많이 사용되므로 꼭 알아두자!
다음 챕터에선 3차원 공간에서 똑같이 divergence와 rotation(Curl)에 대해서 알아보자.
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 부록1. 끝난게 끝난게 아닌 최대/최솟값 찾기 (Lagrange Multiplier) (2) | 2023.01.26 |
|---|---|
| (미적분학) 17-2. 드디어 마지막, 스토크스 정리 (Divergence, Curl in 3D, Stokes' Theorem) (0) | 2023.01.25 |
| (미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치환적분법) (0) | 2023.01.19 |
| (미적분학) 16-2. 그냥 순서대로 적분하면 되는거 아닌가??? (Multiple Integral, Fubini's Theorem) (0) | 2023.01.18 |
| (미적분학) 16-1. 선적분과 비슷한 듯... 면적분 (Surface Integral) (0) | 2023.01.15 |



