다변수함수의 미분 파트에서, 주어진 f(x)의 최댓값과 최솟값을 찾는 방법에 대해서 알아보았다.
-> 이를 그냥 뭉뚱그려서 최적화 문제(Optimization)로 볼 수 있다.
gradient와 hessian을 이용한 방법은 x값에 조건이 없다. 하지만, 실제로 x에는 조건들이 가득하다. (예를 들어서, x 성분이 모두 양수여야 한다 or x의 norm이 1보다 작아야 한다는 등....) 이러한 조건들을 그냥 g(x)<=c (물론 g(x)는 다변수함수도 가능)라고 하자.
(예시)
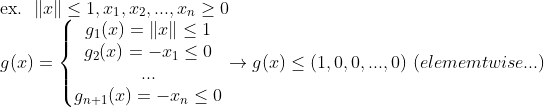
즉, 우리가 원하는 문제상황은 다음과 같다.

즉, g(x)<=c를 만족하는 x에 대해서만 f(x)를 구해야 한다.
물론, equality 조건도 존재할 수 있으므로, 이를 일반화하면 다음과 같이 정리할 수 있다.
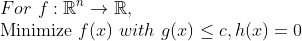
이를 다루는 기법은 KKT condition이라고 한다. 자세히는 살펴보지 않을 것이지만, 미분가능한 함수 f,g에 대해서, 주어진 x 조건이 convex set으로 주어져 있다면 최댓값이나 최솟값은
1. g(x)=c (즉, 경계면(boundary)에 있다.), 혹은
2. h(x)=0
3. f'(x)=0
을 만족하는 점에 존재한다.
(혹시, 예전 교육과정을 밟았던 사람들은, 부등식의 영역이라고 해서 배운 것이 있을텐데, 그 때 결국엔 두 직선의 교점, 혹은 부등식의 경계만 고려했던 것을 생각하면 된다.)
f'(x)=0인 경우에는 trivial이고, f'(x)=0이 아닌 경우에 왜 최대/최소가 경계에 존재해야 하는가는 대충 이렇게 바라볼 수 있다.
만일 f'(x)=0이 되는 지점이 없다면 (g(x)<=c를 만족하는 x에서)
1. f'(x)>0 for all x on {g(x)<=c}
2. f'(x)<0 for all x on {g(x)<=c}
일 것이다. (물론 다변수함수라면, 각 x 성분에 따라서 >0 or <0이 다를 것이다.)
1번이 되었던지, 2번이 되었던지, f(x)는 각 x 성분이 움직임에 따라서 증가나 감소를 일관되게 해야하므로 결국 끝에서(경계에서) 최댓값이나 최솟값을 가질 것이다.
이를 그러면 수식으로 어떻게 표현을 할까?
다음과 같은 식을 생각해보자.
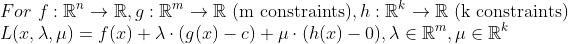
lambda와 mu는 또 다른 변수라고 생각하자. 그러면 다음과 같은 식을 얻을 수 있다.

만약, 부등식과 등식 조건을 모두 만족하는 극점(극대 or 극소)이 존재한다면, 두번째, 세번째 식=0을 만족할 것이다. 또한, 첫번째 식에서 grad f와 equality 조건 항을 합한게 0이 되기 때문에 (Lagrange Multiplier에서 서술) mu에 관한 논의만 하면 된다. 결국에는 첫번째 식도 0이 되는 mu값이 존재하므로 극점이 존재하면 첫번째 두번째 세번째식 = 0 이 된다.
즉, 이는 우리가 기존에 했었던 gradient로 최댓값과 최솟값을 구하는 방법을 그대로 쓸 수 있다는 것을 보여준다.
lambda, mu를 도입하여(차원을 높여서) 제한되어 있던 x 조건을 그냥 풀어줄 수 있다! -> KKT condition....
이 때, 부등식 조건은 없고, 등식조건만 있을 때의 경우 라그랑주 승수법이라고 한다.
(라그랑주 승수법(Lagrange Multiplier))
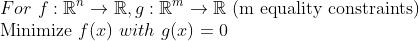
Then, Use Lagrange Function L

이 때, 변수 lambda를 lagrange multiplier라고 부른다. 그러면 다음과 같은 식을 만족할 때, 최댓값 or 최솟값을 가진다.
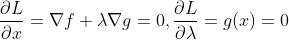
(증명)
만일 점 P가 g(x)=0을 만족하는 set에서 f에 대해서 극점(극대 or 극소)이라고 하면,
1. grad g=0인 경우
-> grad g와 grad f는 linearly dependent (trivial)
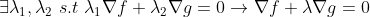
2. grad g=0이 아닌 경우
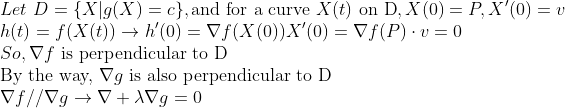
그러므로, 극점이고 두번째 식(lambda 편미분)을 만족하면 첫번째 식(x 편미분)도 만족한다. (lambda가 존재한다!)
첫번째 식을 만족하지 못하면, 극점이 아니거나 두번째 식을 만족하지 못하기 때문에
-> 첫번째 식과 두번째 식을 만족하면 극점(최댓값 or 최솟값)이다!
(예시)
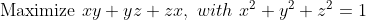
그러면 다음과 같이 Lagrange Function을 잡으면 된다.

Lagrange Multiplier는 사용하는 것이 어렵지 않기 때문에 복잡한 함수의 최댓값, 최솟값을 찾는데 유용하다. (다만, 등식 조건이라는게 안타깝다...) 만일 부등식 조건이 추가가 된다면 KKT를 이용하면 되지만 이 경우엔 주어진 부등식 영역이 convex인 경우에 사용이 가능하다.
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 부록3. 벡터 내적, 외적 공식 더 알아보기 (0) | 2023.01.30 |
|---|---|
| (미적분학) 부록2. 면적분과 물리 (Maxwell's Equations, Navier-Stokes Equation) (0) | 2023.01.30 |
| (미적분학) 17-2. 드디어 마지막, 스토크스 정리 (Divergence, Curl in 3D, Stokes' Theorem) (0) | 2023.01.25 |
| (미적분학) 17-1. 물리학에서 많이 쓰이는 바로 그 정리 (Divergence, Rotation(Curl) in 2D) (0) | 2023.01.25 |
| (미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치환적분법) (0) | 2023.01.19 |



