이번챕터에서는 잘 나오지만, 따로 배우기는 힘든 벡터 공식들에 대해서 알아볼 것이다.
참고로 내적과 외적을 분배법칙처럼 써버리면 안된다!
1.

(Note) abc 순서대로 있을 때 등식 성립....
(증명)
사실, 저 세 식 다 육면체의 부피이다.

axb는 밑면의 넓이가 되고, c와 내적을 하면, axb의 방향이 밑면에 수직이라 육면체의 높이가 된다.
그러므로, 저 세 식 다, 육면체의 부피가 된다. 다만 방향의 문제 때문에 abc가 순서대로 돌 때 등식이 성립한다.
또한, bxc 계산할 때 determinant에서 i,j,k를 그냥 a_1,a_2,a_3로 바꿔버리면 쉽게

임을 보일 수 있다.
2.

(증명)
사실 별건 없고, 성분별로 다 풀어쓰면 된다....

그러나 많이 쓰이는 공식이므로 알아두면 좋다.
3.

rotation 돌면서 다 더하면 0
(증명)

4.

(증명)
2번 식을 쓰면

5.

(증명)
외적의 정의를 이용하면,

또한, 이 표현은 이렇게도 표현 가능하다.

6. Del operator에 관한 표현들(벡터함수의 미분) -> 벡터 내적, 외적 성질과 비교해보자!

(증명)
1. 단지, 곱의 미분법이다...
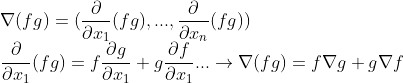
2. 이번에도 단지 곱의 미분법이다.

3. 여기서 중요한건, del의 위치에 따라서 다른 식이 나온다는 것이다!! (위의 벡터인 경우와 비교해야함!!)
Del을 그냥 벡터처럼 다루기는 했지만, del 앞에 나오는 함수는 미분되지 않고, del 뒤에 나오는 식이 미분되므로, del과 함수의 순서가 중요하다.
여기서도 del을 제외한 스칼라 함수와 벡터장은 위의 벡터와 똑같은 성질을 유지한다는 점을 기억하자!
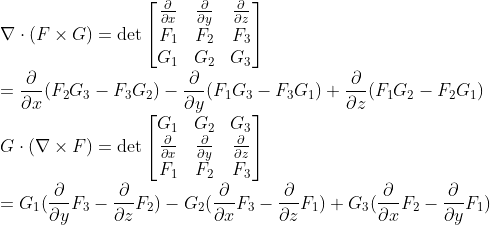
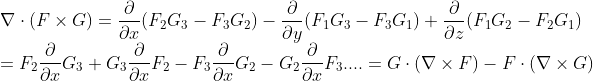
생략하긴 했지만, 다 풀어쓰면 증명할 수 있다.
4. 이 경우에도 3과 마찬가지...

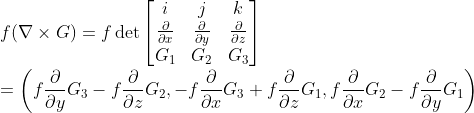
결국 곱의 미분법과 똑같다...
5. 벡터 증명할때와 비슷하게 성분별로 다 풀어서 쓰지만, 단지 저 del의 순서를 체크하면서 전개한다.
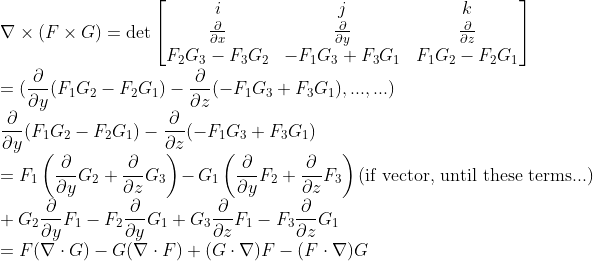
(Note) del이 저렇게 뒤쪽으로 가면???
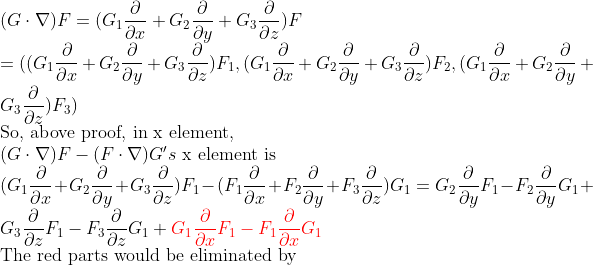
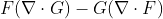
이 공식들은 잘 나오기는 하지만, 나올 때마다 증명하기는 꽤나 귀찮으므로, 알아두면 써먹을 때가 있을 수 있으므로 참고 바란다.
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 부록2. 면적분과 물리 (Maxwell's Equations, Navier-Stokes Equation) (0) | 2023.01.30 |
|---|---|
| (미적분학) 부록1. 끝난게 끝난게 아닌 최대/최솟값 찾기 (Lagrange Multiplier) (2) | 2023.01.26 |
| (미적분학) 17-2. 드디어 마지막, 스토크스 정리 (Divergence, Curl in 3D, Stokes' Theorem) (0) | 2023.01.25 |
| (미적분학) 17-1. 물리학에서 많이 쓰이는 바로 그 정리 (Divergence, Rotation(Curl) in 2D) (0) | 2023.01.25 |
| (미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치환적분법) (0) | 2023.01.19 |



