(해석학 참고링크)
(해석학) 19-1. 다변수벡터함수의 적분... 리만-스틸체스 적분처럼?? (Overview of Integration of MIMO -> Integral on K-cell): https://0418cshyun.tistory.com/91
(해석학) 19-1. 다변수벡터함수의 적분... 리만-스틸체스 적분처럼?? (Overview of Integration of MIMO -> Inte
이번 챕터부터 다변수벡터함수(MIMO)의 적분에 대해서 들어가려고 한다. 이해를 돕기 위해서 일변수함수(SISO)의 적분(리만-스틸체스적분)과 비교해보자... 일단, 먼저 적분을 위해서는 적분 구간(
0418cshyun.tistory.com
지난 챕터에서 면적분에 관련한 이야기를 하였을 때, 다중적분에 대한 이야기가 잠시 언급이 되었었다. 이미 봐서 알겠지만, 그냥 다변수함수가 있을 때, 여러 개의 변수에 대해서 적분하는 것을 그냥 다중적분이라고 할 수 있다.
예를 들어서 이중적분인 경우 다음과 같다.
(Multiple Integral(다중적분)) (n=2)

여기서 S를 bounded(유계)로 잡았는데, 만일 아닌 경우, 특이적분으로 다룬다. (일변수때도, 무한대로 커지는 구간을 잡지는 않았다.) -> 해석학 카테고리 참고
또, S를 S'로 확장시켰는데, 이는 우리가 Delta를 잡을 때, Square 모양으로 잡기 위함이다.
그리고, 그냥 2D가 되어서 면적으로 Delta를 잡을 뿐, 일변수때의 정의와 별반 다를게 없다.
이와 같이, 이중적분, 삼중적분 등도 정의할 수 있다.
또한, n중적분을 다음과 같이 표현하기도 한다.

그리고, 다중적분에서도 일변수함수의 적분때와 성질이 동일하다! 그 중에서 조금 중요한 성질 하나만 살펴보면
(Abstract Value of Integral)

(증명)

f>0인 부분과 f<0인 부분을 나누어서 (f+,f-) 풀면 된다.
이는 n중적분인 경우에도 똑같이 적용될 수 있다.
여기까지 다중적분의 정의에 대해서 살펴보았는데, 실제로 계산을 할 때는 저 위의 정의대로 하는 경우는 거의 없고, 앞 챕터에서 말한 것과 같이, 순차적으로(이중적분이면 x,y나 y,x 순서로) 적분을 하게 된다.
이를 보장해주는 것이 바로 푸비니 정리(Fubini's Theorem)이다.
(Fubini's Theorem(푸비니 정리))

(물론, f가 S에서 적분가능할 때, 각 x,y에 대해서 적분 가능하다는 것은 자명하다. (by definition)
(증명)
1. f가 S에서 적분가능할 때, 각 x,y에 대해서도 적분가능하다.
적분 정의에서 쓴 Partition을 그대로 갖고오자.
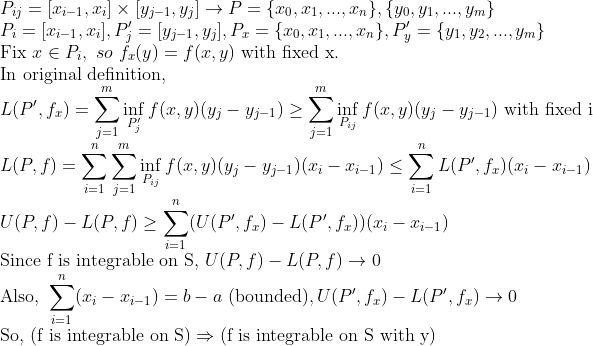
x에 대해서도 동일하게 적용이 가능하다.
2. f가 x,y에 대해서 각각 적분이 가능할 때, S에서도 적분이 가능하다.
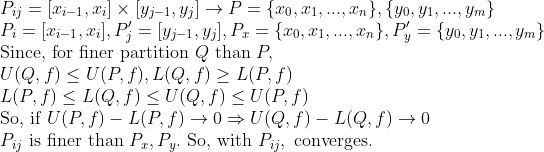
3. 등식 증명
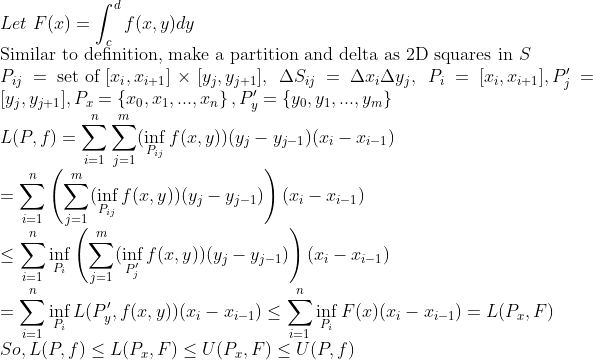
즉, F를 x방향으로 적분한 것과 이중적분은 값이 동일하다는 것을 알 수 있다.
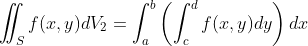
적분 순서가 바뀐 것도 동일하게 할 수 있다.
여기서 더 나아가서, f를 x에 대한 함수와 y에 대한 함수로 쪼갤 수 있다면, 다음과 같이 쓸 수도 있을 것이다.
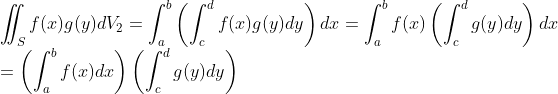
즉, 각각에 대해서 적분할 수 있다.
사실, 여기서는 적분 순서를 그냥 바꾸어주었지만, 원하는 구간 S가 x,y에 대해 상수로 주어져 있지 않을 수 있으므로, 무턱대고 바꿀수는 없는 노릇이다.
예를 들어서 다음과 같은 문제를 생각하자.
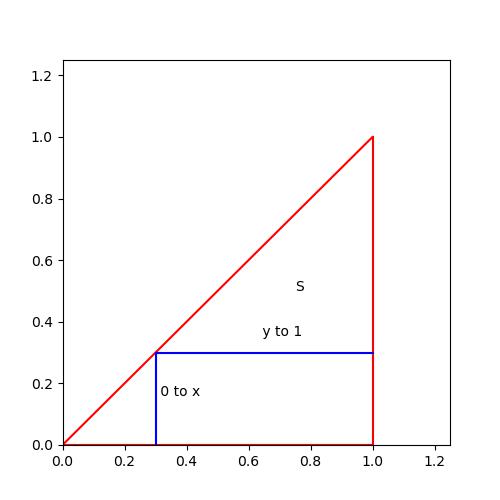
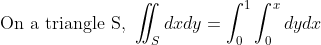
그러나 다음 식은 말이 안된다...
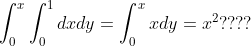
왜냐하면 적분 구간을 고려하지 않았기 때문이다. (순서 바꾸고 난 후의 적분에서 바깥 적분이 x에 대한 함수로 나오면 안되지!)
그러므로, 적분 구간을 고려하면서 (주어진 S를 그대로 보존하면서) 바꿔야 한다.
만일 적분구간을 바꾼다면 (즉, x부터 적분한 뒤, y 적분) 범위를 바깥쪽부터 고려해야 위와 같은 상황이 발생하지 않을 것이다.
y의 범위는 0부터 1일것이고, x의 범위는 y에 대한 함수로 나오면 될 것이다. 즉, 아래 그림을 참고하면, x는 y부터 1까지 범위를 잡으면 된다.
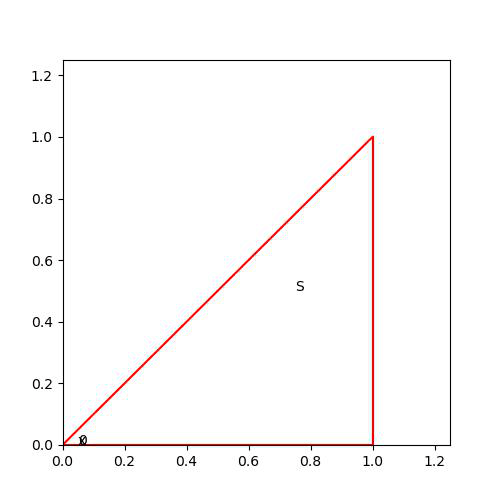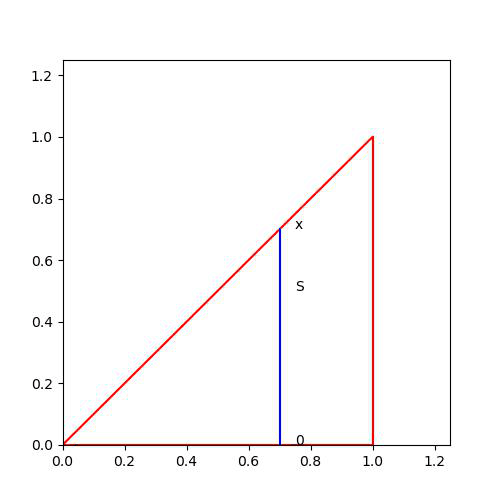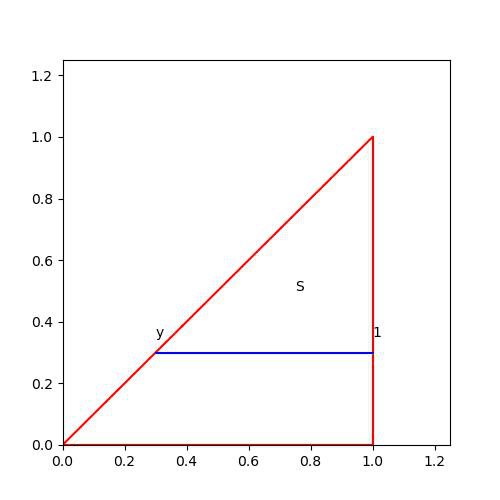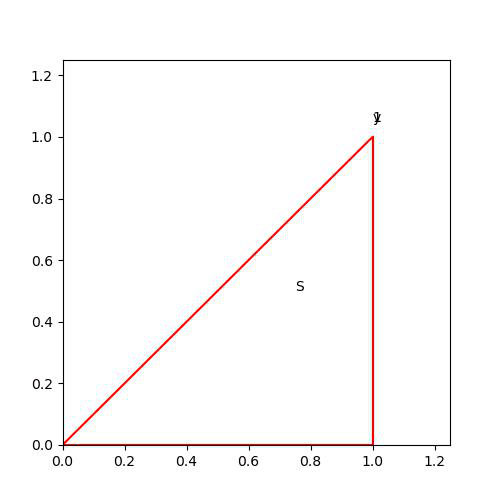
그래서 우리가 구하고자 하는 적분은 다음과 같다.
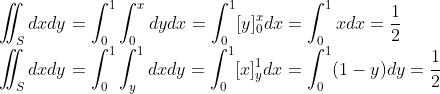
오늘은 다중적분에 대한 개념과 푸비니 정리, 특히 적분 순서 바꿀때, 범위를 고려하면서 바꿔야 한다는 것을 알아보았다.
다음 챕터에서는 선적분, 면적분에서 살짝 짚고 넘어간 치환적분법, 특히 좌표계를 바꿀 때 Jacobian이 다중적분에 어떤 영향을 미치는지 알아본다.
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 17-1. 물리학에서 많이 쓰이는 바로 그 정리 (Divergence, Rotation(Curl) in 2D) (0) | 2023.01.25 |
|---|---|
| (미적분학) 16-3. 계속 나오는 데에는 이유가 있지 (좌표계 변환과 치환적분법) (0) | 2023.01.19 |
| (미적분학) 16-1. 선적분과 비슷한 듯... 면적분 (Surface Integral) (0) | 2023.01.15 |
| (미적분학) 15-3. 더더, 선적분 (Fundamental Theorem in Line Integral, Potential Function) (0) | 2023.01.13 |
| (미적분학) 15-2. 더, 선적분 (Length of line, Curvature) (0) | 2023.01.13 |



