이번 챕터에서는 미적분학의 기본정리(Fundamental Theorem of Calculus)와 적분 나머지 파트들을 정리할 것이다.
먼저, 미적분학의 기본정리부터 살펴보자.
(적분과 미분과의 관계)
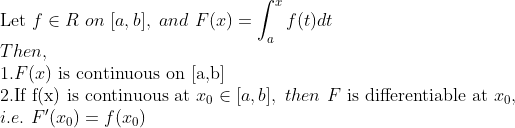
특히, 2번이야 워낙에 잘 알고 있는 성질이지만, 적분결과가 연속이라는 것도(닫힌 구간이라 Uniformly continuous) 꼭 알아두자!
(증명)
1. 연속의 정의를 이용하자!
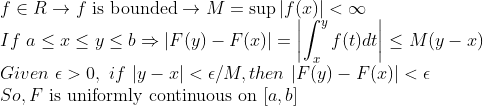
2. F'(x)를 유도해보자!
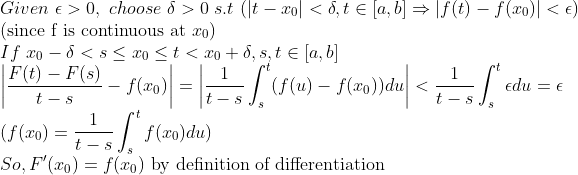
(Corollary)
(Fundamental Theorem of Calculus(미적분학의 기본정리))
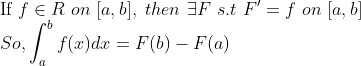
여기서 알아두어야 할 것은 F가 유일하지는 않다는 것이다!(부정적분에서 상수항이 추가되는 것을 생각하자)
(증명)
존재성은 위에서 증명을 하였고, 아래줄의 등식만 증명하면 된다!
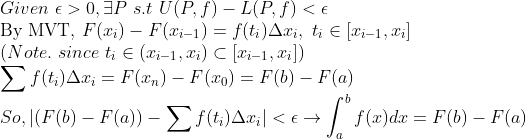
(계속 MVT가 등장한다! -> 기억 안 난다면 다시 한번 보고 오자!)
(적분가능하니까 계속 sup,inf 안 쓰고 구간 안의 임의의 점을 이용한다! -> 이부분 역시 기억 안 난다면 보고 오자!)
이로 인해서 정적분의 계산이 아주 편해진다!!!
(물론, 이미 알고 있어서 정적분을 급수를 이용해서 계산한 적이 거의 손에 꼽을 정도이겠지만, 우리가 온 흐름대로 보면 아주 유용한 정리가 된다!)
이번에는 미적분학의 기본정리를 이용해서 부분적분법(Integration by parts)을 증명해보자
(Integration by parts)(부분적분법)
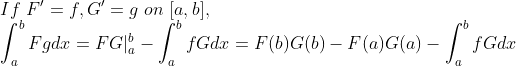
(증명)
미적분학의 기본정리를 쓰면 아주 간단하다!
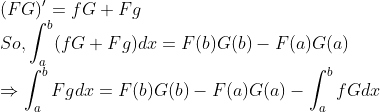
이번에는 간단하게 다변수함수의 적분에 대해서 생각해보자... (더 자세한 내용은 뒤에서 다룰 예정!)
(미적분학 카테고리 -> chap 14 이후 참고!)
미적분학 카테고리에서 본 것을 생각해보면
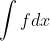
에서, f가 벡터함수(n-dim), dx도 벡터함수(m-dim)였고, 저 적분값은 항상 실수차원으로 나타내려고 한 것(절댓값이나 내적을 이용해서 1차원으로 끌어내림....)을 알 수 있을 것이다.
이는, 미적분학에서 선적분이나 면적분의 설명을 위해서 그랬었고, 생각해보면... 굳이 적분값이 실수차원일 필요는 없다! -> 벡터여도 상관 없다....
여기서도 일단은... , 저 dx만 1차원이라고 생각하자. -> 즉, fdx는 그냥 실수 곱이라고 생각하면 된다. (내적이 아니라!)
그럼 정의를 다음과 같이 할 수 있을 것이다.
(Integration of Multi-dimension function)
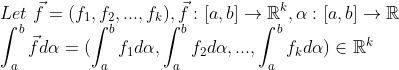
이런 식으로 정의하면 우리가 보아왔던 적분에서의 정리들이 대부분 성립한다! (alpha가 1차원이라 각 차원마다 증명 그대로 적용이 가능하다!)
예를 들어서,
1. 미적분학의 기본정리
2.
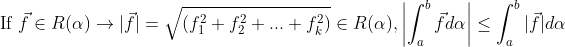
도, Multi-dimension에서 성립한다! (증명은 Trivial하니 생략!)
특히, 미적분학에서 많이 본 Curve의 개념도 여기서 생각해보자!
(미적분학 참고링크)
(미적분학) 15-1. 다변수함수의 적분의 예시 없나요??? (Curve, Line Integral): https://0418cshyun.tistory.com/21
(미적분학) 15-1. 다변수함수의 적분의 예시 없나요??? (Curve, Line Integral)
지난시간에는 다변수함수의 적분, 특히 적분 구간에 다변수함수가 들어갈 수 있다는 것을 설명하였다. 이번에는 구간에 들어가는 다변수함수의 예를 생각해보려고 한다. 이 때, 구간에 들어가
0418cshyun.tistory.com
(Curve)(곡선)
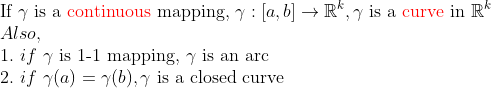
즉, 닫힌구간에서 연속이면 -> Curve.
1. curve이고, 1-1 mapping(즉, 함숫값이 겹치지 않는다!) -> Arc
2. curve이고, 끝점의 함숫값이 같다. -> Closed curve
또한, 곡선의 길이는 다음과 같이 정의한다.
(Length of Curve)
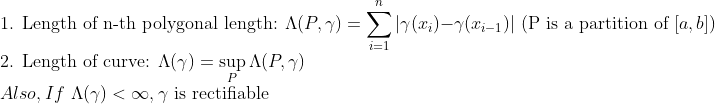
이미 Partition에 대해서 배웠으니, 이해하는데는 무리가 없을 것이다..
-> gamma를 리만-스틸체스 적분의 alpha처럼 생각할 수도 있을 것이다!
물론, 곡선의 길이를 이렇게 구하는 경우는 거의 없을 것이고 다음과 같이 구할 것이다.
(Length of Curve and Derivative of Curve)
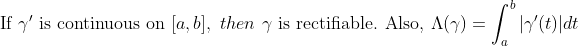
(증명)
곡선의 길이가 적분값보다 작거나 같다는 것을 증명하고, 반대로 곡선의 길이가 적분값보다 크거나 같다는 것을 증명한다.
그러므로 곡선의 길이는 적분값과 같다!
1.
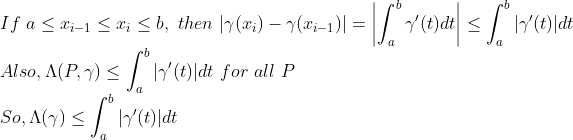
2.
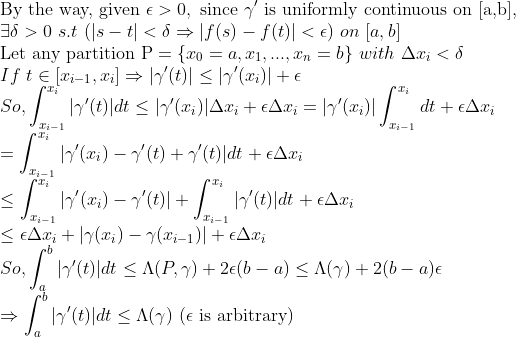
3. So,
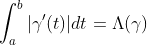
여기까지 리만-스틸체스 적분에 관한 이야기를 해보았다.
Partition에 대한 내용 정도만 새로울 것이고, 나머지는 결과는 다 알고 있었기 때문에 싱거울 수도 있었을 것이다...(물론 쉽다는 얘기는 아니다)
그리고, 여기까지 왔으니 꼭 다시 한번 미적분학 카테고리를 보자. 아마 퍼즐이 맞춰지는 기분일 것이다!
다음챕터에서는 특이적분(구간이 무한대...?)과
자꾸 적분가능하다는 표현을 다음과 같이 썼는데
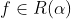
이 표현이 정확히 무엇을 뜻하는지에 대해서 알아보는 시간을 간략하게(부록으로) 다룰 것이다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) Summary 2. 수열부터 적분까지 (0) | 2023.02.21 |
|---|---|
| (해석학) 8-5. 아직 좀 부족한데....? (Improper Integral, Space of Riemann-Integrable ftns) (0) | 2023.02.21 |
| (해석학) 8-3. 리만-스틸체스적분인데, 리만적분만 하는 느낌...? (Heaviside Unit Function, Change of Variable) (0) | 2023.02.19 |
| (해석학) 8-2. 언제 리만적분이 가능하지? (Existence of Riemann Integral) (0) | 2023.02.18 |
| (해석학) 8-1. 적분을 제대로 정의해보자! (Riemann-Stieltjes Integral) (0) | 2023.02.17 |



