이번 챕터에서는 리만(스틸체스) 적분의 적분가능성에 대해서 더 알아보고, 나머지 적분한 함수의 성질을 보도록 한다.
먼저, 적분가능성을 살펴보자. 적분이 가능할 때는 Upper Integral과 Lower Integral이 같은 경우이다.
그러면, 이를 Partition의 관점으로 보았을 때
Partition이 더 잘게 쪼개질 수록 -> Upper Integral과 Lower Integral이 비슷해진다.(차이가 0에 가까워진다.)
어디서 많이 본 느낌 아닌가? -> 코시수열, 혹은 입실론 - 델타 논법이 떠오르면 된다!
즉, 다음과 같이 설명할 수 있다..
n이 증가할수록 차이가 0에 가까워진다 -> 코시수열
----> P가 더 잘게 쪼개질수록 차이가 0에 가까워진다. -> 적분가능성
(Existence of Riemann(Stieltjes) Integral)

이러한 논법은 극한을 다룰 때 많이 다뤄보았으므로, 모든 Partition에 대해서 다 찾아서 upper, lower integral을 구하는 것(기존의 정의)보다 훨씬 쉽다...
(증명)
1. ->
Upper / Lower Integral을 구할 때의 각각의 Partition의 Refinement를 생각하자

2. <-
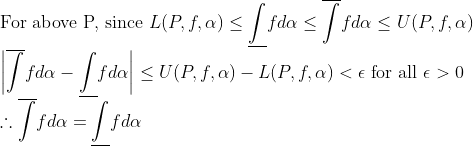
그런데, 저 U와 L을 구할 때, 잘게 자른 구간마다 sup f(x)와 inf f(x)를 구하기가 상당히 까다로울 수도 있다.
그래서 이를 그냥 f(x)로 어떻게 안되나... 생각할 수도 있다. 왜냐면 만약에 적분가능하면 어차피 U와 L이 얼마 차이도 안나기 때문에...
그런데, U가 sup이고, L이 inf이었던 것을 생각하면 다음과 같이 생각할 수 있다.

U,L이 각각 sup, inf으로 정의되었던 것을 생각하면 금방 증명할 수 있다!
(특히 1번은 앞 챕터에서 이미 나왔다!)
여기까지, 적분가능성을 입실론-델타 논법처럼 생각할 수 있는 것을 보았고,
이제부턴 각 상황에 따라서 적분가능성을 판단해볼 것이다.
1. 연속함수
함수 f가 닫힌구간 [a,b]에서 연속이면 적분가능하다!

연속파트에서 연속을 제대로 정의했으니 증명해보자!
(증명)
닫힌 구간에서 f가 Uniformly Continuous라는 것을 이용한다!
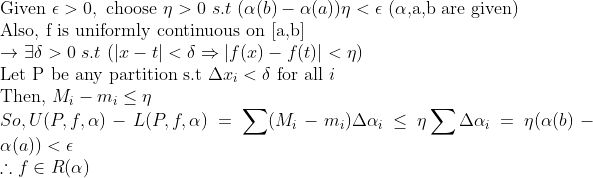
2. 단조함수
함수 f가 [a,b]에서 단조함수이고, alpha가 연속단조함수이면(앞에서는 연속조건이 없어도 되었었다!) 적분가능하다!
(증명)
f가 단조증가함수인 경우에

n을 크게 잡으면 어떤 epsilon에 대해서도 작아진다는 것만 확인하면 된다!
이 때, alpha가 연속,단조함수라는 조건은 맨 처음 Partition을 나눌 때에 중간값정리를 쓸 때 이용한다.

f가 단조감소여도 똑같이 증명할 수 있다!
(Corollary) 위의 성질들을 이용하면 다음과 같은 성질을 얻는다.

여기서 f가 심지어 monotonic도 아니고, 연속도 아니라는 점을 주목하자!
(물론, finite개수 불연속점이라서 대부분은 연속일 것이다!)
(증명)

유한개의 불연속점의 집합을 E라고 하였을 때, 불연속점을 감싸는 작은 구간(닫힌구간) [u_i,v_i]를 잡자. (이 구간들은 겹치지 않도록 작게!)
그리고 [a,b]에서 끝 점(a,b)이 겹치는 경우 빼고, (u_i,v_i)(열린구간)를 [a,b]에서 빼자.
만약에 끝점이 불연속점인 경우엔(a가 불연속이라고 가정해보자!) [a,v_1)을 [a,b]에서 빼자.
그럼 남는 구간은 불연속점은 쏙 다 빠지므로 남는 구간의 각 부분구간(닫힌구간)에서 f는 연속이라서 각 부분구간에서 적분이 가능하다!
여기서는 그렇게 하지 않고 연속구간, 불연속구간을 한방에 증명한다.

일단, K에서 균등연속에 의해 delta를 구할 수 있고, Partition P를 잡는데
1. u_i,v_i가 P의 원소
2. u_i,v_i사이의 값이 P에 들어가지 않음! (불연속 구간을 더 나누지 않는다.)
3. 모든 x_i 사이의 차이를 delta보다 작게!
-> u_i,v_i는 불연속점만 포함하도록 잡으면 되므로, delta보다 작게 잡을 수 있다!
그러면 P의 모든 부분구간들은 K에 포함이 되거나, K에 포함이 안되거나... 일 것이다.
먼저 K에 포함이 된다면 -> Uniform Continuous에 의해서 구간 안에서 어떤 두 점을 잡아도 f값의 차이는 epsilon보다 작다.
K에 포함이 안된다면 -> 즉, x_(i-1),x_i가 각각 u_i,v_i이므로 위에서 u_i,v_i를 잡을 때의 조건에 의해서 alpha값의 차이가 epsilon보다 작다.
그러므로 U-L을 했을 때, K에 포함되는 구간, 안되는 구간을 나누어서 더하면 위와 같이 결과가 나오고, 어차피 epsilon에 상수배 한 것은 아무 의미 없으므로, 주어진 아무 epsilon에 대해서 U-L<epsilon 이 되는 Partition P를 잡았다!
그러므로 적분가능하다!
그림으로 보면

즉, 연속인 구간 K는 이미 적분 가능한 것을 알고 있고,
불연속인 구간은 구간을 아주 작게 잡아서(<epsilon) 적분값(U,L)을 거의 0이 되도록 잡는 것이라고 생각하면 된다!
그러므로 Infinite개수의 불연속점이 생길 때에는 이런식으로 적분가능성을 판단할 수 없을 것이다... 0*inf =????
참고로 이런식의 접근(적분가능한 부분 / 불가능한 부분 -> 0)은 자주 쓰인다!
(Corollary)
f가 [a,b]에서 Piecewise-Continuous이면 리만적분가능하다! (alpha=x)
여기서 하나 짚고 넘어갈 것은, f와 alpha가 동시에 불연속인 지점이 있다면 적분불가능 할 수도 있다!
사실, 아직까진 alpha에 대해서 크게 와닿지 않겠지만, alpha를 잘 활용한다면 적분을 되게 쉽게 할 수도 있기 때문에 -> (사실상 치환적분법이긴 하지만...) 알아두고 넘어가자!
3. 합성함수

f가 연속이 아니더라도, 적분가능하고, g가 닫힌구간에 대해서 정의될 수 있다면(즉, Range of f가 bounded...) 합성함수 h도 적분가능하다는 내용이다.
(증명)
이 경우에도 위의 Corollary 경우와 동일하게 문제 없이 적분하는 구간(A)과 문제 있는 구간(B)을 나누어 증명한다!

이번에도 함수값을 epsilon으로 못 줄이는 부분(B)은 구간을 delta보다 작게 줄여버린다.

다시 한번 강조하지만, Corollary와 여기서 쓴 증명방법은 꽤 많이 쓰는 방법이라 알아두면 좋다!
지금까지 리만스틸체스적분 가능성에 관한 내용을 다루었는데, 결과는 아마 이미 알고 있는 것이 많았을 것이다. (piecewise 연속이면 적분가능 같은 것...)
다음시간에는 아직까지 별로 관심을 주지 않은 alpha에 대한 내용을 다룰 것이다.



