이번 챕터에선 미분방정식의 해(Initial Value Problem의 해)가 유일하다는 것을 증명하려고 한다. (존재성은 나중에!)
아직 미분방정식에서 자세히 모르거나, 별로 관심이 없다면 패스해도 상관이 없다!
물론, 굉장히 특수한 경우만 다루려고 한다.
1. 편미분방정식 No.... -> 상미분만 다룸!
2. Explicit 꼴만... (y'=f(x,y), not f(x,y,y')=0)
그러나, 미분방정식이 굳이 선형일 필요까진 없다... -> 비선형도 가능!
물론, 대부분의 경우가 편미방이기도 하고, Implicit 꼴을 항상 Explicit 꼴로 바꿀 수는 없긴 해서, 굉장히 특수한 경우이긴 하지만, 그래도 비선형도 다룰 수 있다는게 어디인가....
먼저, 증명하기 전에 다음 Lemma부터 확인하자.
(Lemma)
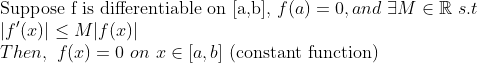
시작점에서 f(x)=0이 되버리니, f'(x)가 계속 0이 되어 상수함수가 된다고 생각하면 된다!
(증명)
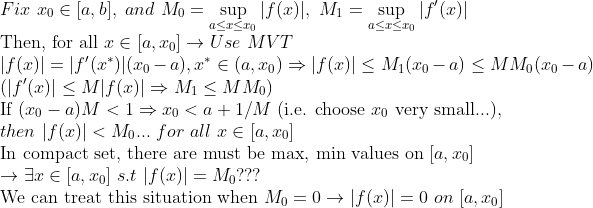
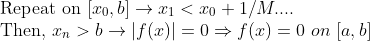
먼저, 위에서 모순 상황이 생기는데, 만약에 M_0가 0이면, x_0를 위처럼 작게 잡아도, |f|<M_0로 나오는 게 아니라, 그냥 |f|=0으로 나오므로, 모순상황이 해결 된다.
그러므로 MVT를 써서, x_0가 a+1/M보다 작으면 [a,x_0]에서 f=0이라는 것을 알았는데, 이 것을 반복하면 간격이 1/M이기 때문에 언젠간 b를 넘어선다. -> 그러므로 [a,b]에서 f=0이다.
이제부터 미분방정식의 해의 유일성(not 존재성...)을 증명해보자.
1. 간단한 y=f(x)인 경우!
(Initial Value Problem(IVP))
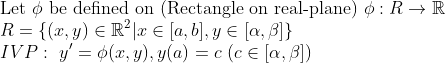
이 IVP의 해가 존재한다고 하자...(존재성 증명 아님)
그럼 이 해(Solution)은 다음과 같다.
(Solution)

그러면 여기서 이 Solution이 유일하다는 것을 증명하자!
(Uniqueness of Differential Equation 1)

-> 즉, 평균변화량이 bounded 되어 있다면
-> 이러한 조건을 만족하는 함수를 Lipschitz-Continuous Function(립시츠 연속함수)라고 한다.
-> 잘 생각해보면, Uniformly Continuous에서 조금 더 나아간 것(빡센 조건)이라고 생각할 수 있다!
(증명)
증명은 의외로 간단하다!
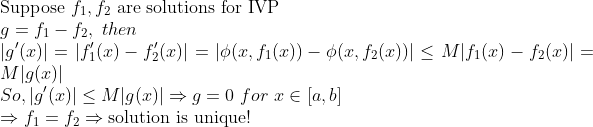
2. Systems of Differential equation
고차미분방정식(High-Order differential equation)을 System of Differential Equation으로 고칠 수 있으므로, 어떻게 보면 고차미방에 관한 해의 유일성이라고 해도 되겠다!
이번에도 똑같이 접근해보자!
(Initial Value Problem(IVP))
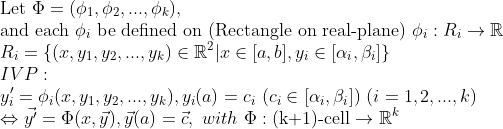
(Solution)
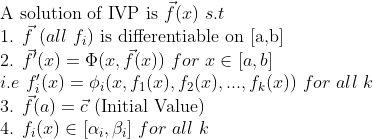
(Uniqueness of Differential Equation 2)
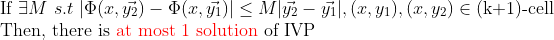
(증명)
증명도 위와 똑같다!

자, 여기까지 특수한 경우(상미분, Explicit 꼴)의 미분방정식의 해의 유일성에 대해서 알아보았다.
주어진 문제가 립시츠 연속을 만족하면 해가 유일하다는 것을 보였다.
립시츠 연속조건이 꽤나 까다롭다는 것이 문제인데...(균등연속보다 더 함...) 일단, 유일성을 증명한게 어디인가...
다음 챕터부터는 적분에 관한 이야기를 시작한다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 8-2. 언제 리만적분이 가능하지? (Existence of Riemann Integral) (0) | 2023.02.18 |
|---|---|
| (해석학) 8-1. 적분을 제대로 정의해보자! (Riemann-Stieltjes Integral) (0) | 2023.02.17 |
| (해석학) 7-1. 미분이 여기서 가장 쉬움.... (Differentiation of 1-variable function) (0) | 2023.02.16 |
| (해석학) 6-4. 연속에 대한 생각을 넓혀주는 불연속... (Discontinuity) (0) | 2023.02.15 |
| (해석학) 6-3. 연속함수의 성질 Part 2. (Uniformly Continuous) (0) | 2023.02.15 |



