(미적분학 참고링크)
-함수의 극한과 연속-
(미적분학) 3-2. 근데 우리가 필요한건 수열보단 함수 아니었나?? (Convergence, Continuity of function): https://0418cshyun.tistory.com/23
(미적분학) 3-2. 근데 우리가 필요한건 수열보단 함수 아니었나?? (Convergence, Continuity of function)
미적분학에서 사실 실제로 미적분에 이용할 것은 수열이 아니라 함수이다. 저번 챕터까지는 수열의 극한에 대해서 살펴보았고, 이번 챕터에서는 함수의 극한과 연속에 대해서 살펴보자. 함수의
0418cshyun.tistory.com
이번 챕터에서는 함수의 연속성(Continuity)에 관해서 이야기 해보자. 이를 위해서 함수의 극한(Limit of Function)에 대해서 잠시 알아볼텐데, 이미 수열과 급수의 극한에 대해서 알아보았기 때문에, 문제 없이 이해할 수 있을 것이다!
그러나, 중요한 챕터이니 꼭 확실하게 알고 넘어가자!
(Limit of Functions(함수의 극한))
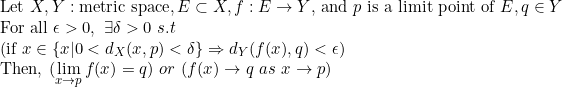
여기서 d_x, d_y는 각각 X, Y에서의 metric을 뜻한다. -> 실수뿐만이 아니라, 일반적인 Metric Space에서 성립한다는 것을 주목하자.
그림으로 보자면
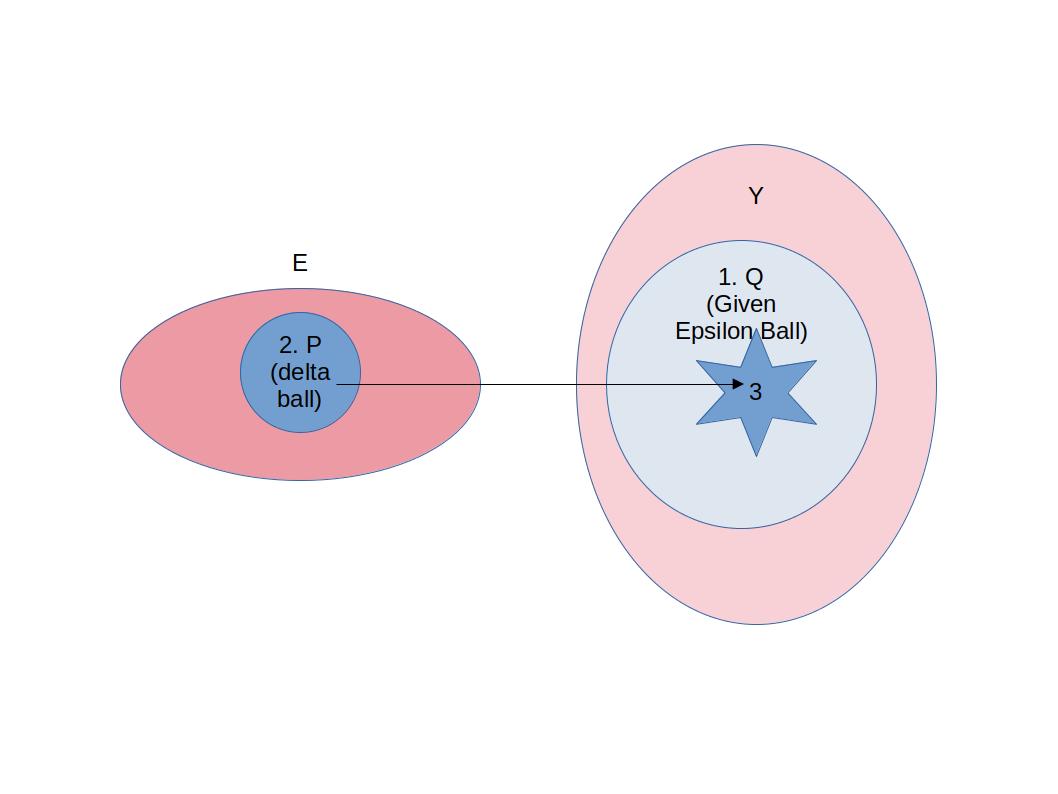
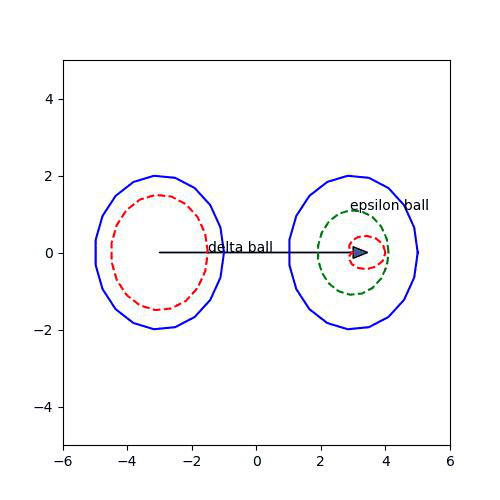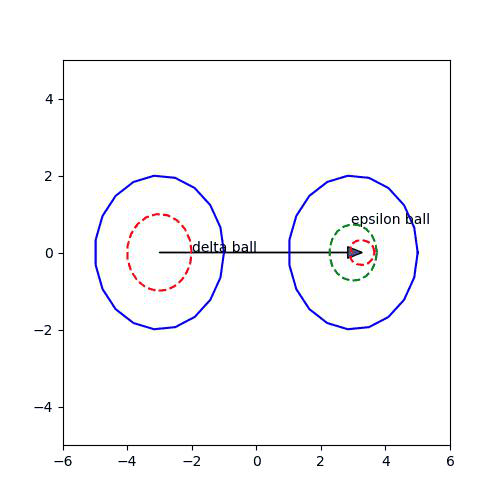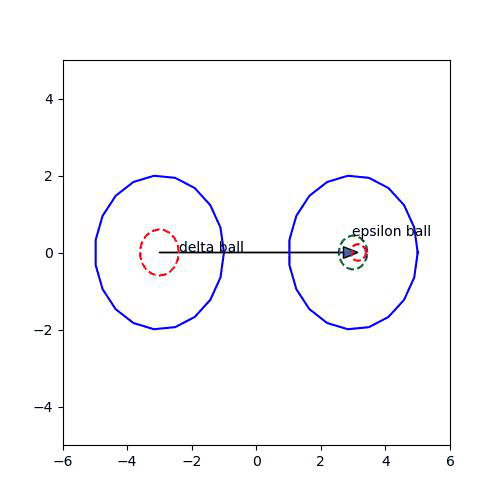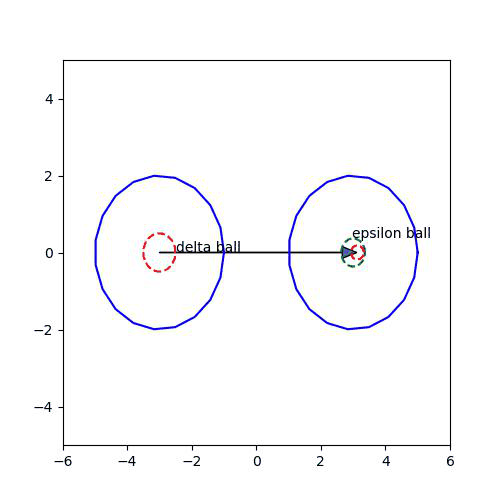
저 위의 정의를 풀어서 얘기하면,
모든 epsilon에 대해서 -> Given epsilon! (이 말이 이해가 안된다면 미적분학 카테고리에서의 입실론-델타 논법 참고)
1. epsilon이 주어져 있을 때, Q를 중심으로 한 반지름이 epsilon인 ball이 있다면,
2. E 안의 어떤 limit point P에 대해서 반지름이 delta인 ball를 잡는데
3. delta ball을 f를 통해서 mapping한 결과가 1번의 ball 안에 들어간다면.. -> 즉, 이러한 delta를 잡을 수 있다면!
f(x) -> Q as x -> P 라고 할 수 있다.
여기서 잠깐 주목해야할 건, p가 E의 limit point라는 것이다...
즉, E를 어떻게 잡았나에 따라서 p가 E에 존재하지 않을 수도 있다! (f가 E에서 정의되어 있는데도!!!!)
(Example 1)
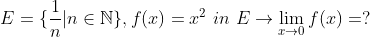
분명히 x=0은 E에 존재하지 않지만, 구할 수는 있을 것이다... 물론 우리가 알고 있듯이 답은 0이다.
정의에 따라서 생각해보면...
1. epsilon=0.1 -> 우리가 delta를 1/3로 잡는다면 delta ball 안의 모든 E의 원소는 1/4,1/5,1/6.....
그러면 mapping한 결과는 1/16,1/25,.....<1/10=epsilon
2. epsilon=0.01 -> 우리가 delta를 1/10로 잡는다면 delta ball 안의 모든 E의 원소는 1/11,1/12,1/13,....
그러면 mapping한 결과는 1/121,....<1/100=epsilon
3. epsilon을 어떻게 잡든간에 delta를 잘 잡으면 mapping 결과를 epsilon보다 작게 할 수 있다!
(사실은)
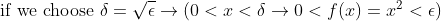
(Example 2)
그렇다면 여기에서 부정은 어떻게 될까??

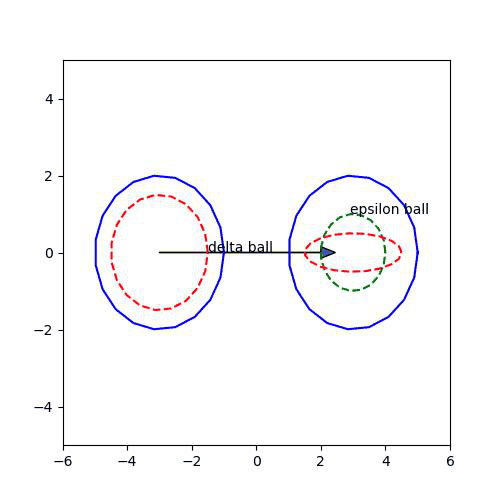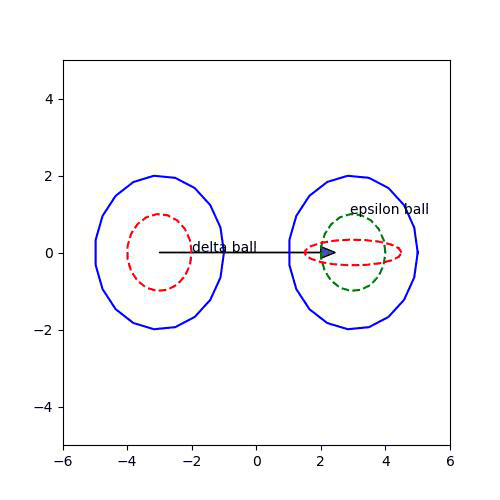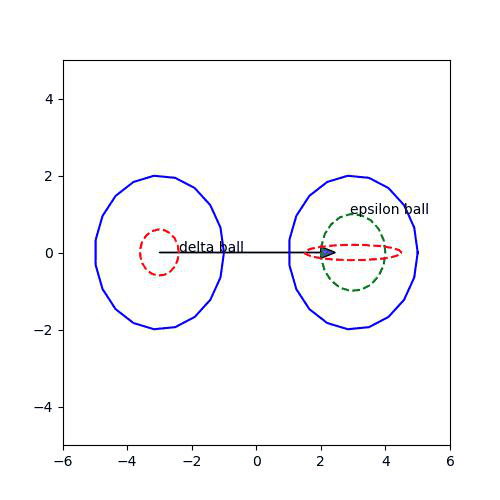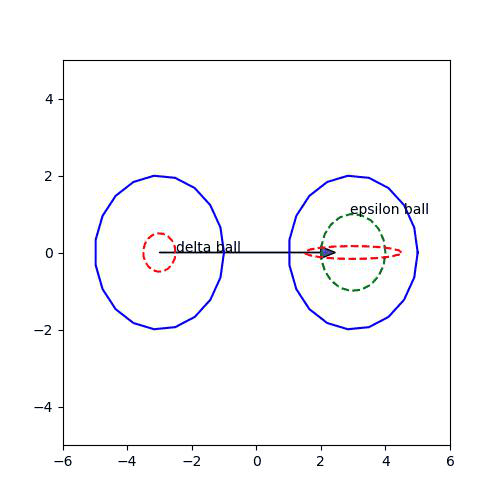
어떤 epsilon에 대해서 delta를 어떻게 잡던지, mapping 결과가 epsilon ball의 밖에 있는 경우가 있는 것을 보이면 된다.
예를 들어서,
1. epsilon=1 -> Epsilon ball : -0.9<y<1.1
delta=0.1: 0<x<0.1 -> 0<x^2<0.01... -> Epsilon ball 안!
------> 그러므로 이 epsilon의 경우는 부정을 보이는데에 실패....
2. epsilon=0.01 -> Epsilon ball : 0.09<y<0.11
delta=0.1 : 0<x<0.1 -> 0<x^2<0.01... -> Epsilon ball 밖!
delta=1: 0<x<1 -> Epsilon ball 밖!
delta=0.0001 : 0<x<0.0001 -> Epsilon ball 밖!....
------> delta를 어떻게 잡아도 epsilon ball 안으로 못 들어가므로, 부정을 보이는데 성공!
함수의 극한과 수열의 극한은 다음과 같은 관계가 있다고 할 수 있다.
(Limit of Function, Sequence)

(증명) -> 극한의 부정에 대해서 꼭 알고 가자!
1. -> 위의 정의에서 p가 E의 limit point였다는 것을 생각하면 당연한 결과이다!
2. <- 대우를 생각해보자!
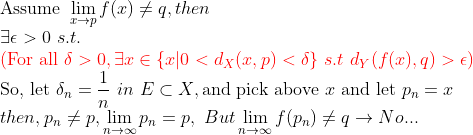
이해를 돕기 위해서 다시 설명하면
만일, lim f(x)가 q가 아니라면... 함수의 극한 정의의 부정을 해야 하는데...(빨간 부분...) 이해 안되면 위에서 Example 2를 참고하자!
극한 정의:
주어진 epsilon(모든 epsilon)에 대해서 (delta ball의 mapping 결과가 epsilon ball로 들어가는) delta를 구할 수 있다!
-> 그렇다면 부정은???
주어진 delta(모든 delta)에 대해서 (어떤 delta ball의 원소가 epsilon ball로 못 들어가는) epsilon이 있다!
어쨌든, lim f(x)가 q가 아니니, 어떤 epsilon에 대해서는, delta를 어떻게 잡아도 delta ball의 원소가 epsilon ball로 못 들어가는 경우가 발생한다. -> Example 2와 그림을 참고하자!
그러면 그 epsilon는 주어졌다고 생각하고, delta를 위의 Example 2에서 잡았던것처럼 delta=1,1/2,1/3,....=1/n으로 잡아보자.
그러면 그 때마다, delta ball의 원소가 epsilon ball에 못 들어가는 경우가 생긴다...
그런데, delta는 점점 작아지므로, delta ball이 p에 수렴하게 된다. (Example 2의 그림에서 delta ball의 중심이 p라고 생각하면 된다...) 그러나 그 delta ball은 언제나 epsilon ball 안으로 못 들어가는 경우의 수가 생긴다. 즉, lim f(p_n)이 q가 될 수는 없다...
그러므로, 대우가 증명이 된다.
그러므로, 함수의 극한에서도, 수열의 극한에서 했던 내용 그대로를 그냥 사용할 수 있다!
(예를 들어서, 수열의 극한이 unique하다는 내용... -> 함수의 극한도 unique하다...)
드디어, 함수의 연속에 대하여 설명한다.
(Continuity of Function)(함수의 연속)
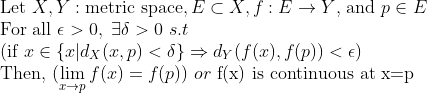
위와 달라진건, 단지 p가 E의 limit point에서 E의 점으로 바뀐 것뿐이다... (f(p)가 정의되려면 어쩔 수 없음)
당연히, p가 E의 점이고, 동시에 E의 limit point라면, 함수의 극한과 연속은 동일하다!
이미 알고 있는 내용들 중 사소한 건 패스한다!!! (함수의 극한의 합과 곱이라던지....)
연속함수의 성질들 중 Topology에 관련된 내용들은 다음 챕터에서 다루고, 여기서는 연속함수 자체의 성질 하나만 짚고 넘어가자..
(Composition of Continuous Function)(합성함수의 연속성)
f, g가 연속함수인 경우, h=g(f(x))는 연속이다
보다 정확하게는,
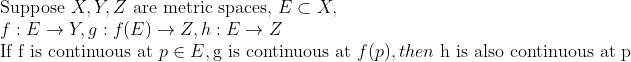
이미 합성함수가 연속인 것은 알고 있겠으나, 여기서 엄밀하게 증명해보자.
(증명)
차근차근 연속의 정의를 써서 증명해보자.
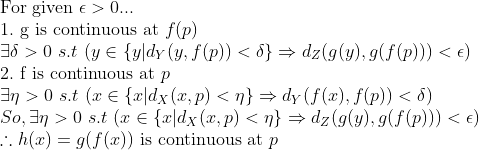
여기까지, 함수의 극한과 연속에 관한 정의를 살펴보았다.
다음챕터에서는 앞서 말한것과 같이 topology와 관련된 연속함수의 성질들을 다루어 볼 것이다. 그리고 드디어 문제의 최대최소정리를 증명하도록 하겠다!!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 6-3. 연속함수의 성질 Part 2. (Uniformly Continuous) (0) | 2023.02.15 |
|---|---|
| (해석학) 6-2. 증명 못 했던거 오늘 다 풉니다... (최대최소정리, 중간값정리) (0) | 2023.02.15 |
| (해석학) 5-3. 나머지 급수 이야기 (Power Series, Rearrangement) (0) | 2023.02.13 |
| (해석학) 5-2. 시그마(급수)는 막 곱하면 안 되나??? (Convergence of Series 2) (0) | 2023.02.13 |
| (해석학) 5-1. 급수부턴 수월함.... (Convergence of Series 1) (2) | 2023.02.12 |



