(미적분학 참고링크)
(미적분학) 2-1. 입실론-델타논법으로 수렴성 증명은 귀찮아 (Comparison Test, Ratio Test, Root Test, Integral Test) :
https://0418cshyun.tistory.com/4
(미적분학) 2-1. 입실론-델타논법으로 수렴성 증명은 귀찮아 (Comparison Test, Ratio Test, Root Test, Integral
(해석학 참고링크) -최소상계/최대하계(sup, inf)- (해석학) 1-1. 도대체 뭐가 문제라 증명을 못했을까? (What is Real Number?) : https://0418cshyun.tistory.com/14 (해석학) 1-1. 도대체 뭐가 문제라 증명을 못했을까
0418cshyun.tistory.com
이번 챕터에서는 앞에서 배운 성질들을 바탕으로, 급수의 수렴성에 대해서 알아볼 것이다.
사실, 미적분학에서 새로 나가는 건 거의 없고, 그저 미적분학에서 스리슬쩍 넘어간 증명들만 다시 한번 볼 것이다...
일단, 급수(Series)라는 건, 이미 알고 있듯이
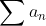
이 것을 말하는데, 수렴처럼 생각하기 위해서 부분합(Partial Sum)을 생각한다. 즉,
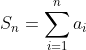
그러므로, 이 급수가 수렴한다는 건 저 부분합이 수렴한다라는 이야기와 동일하다.
앞에서 배운 걸 이용한다면, 저 급수가 수렴하는지 보려면 다음과 같은 방법이 있을 것이다.
1. 코시수열인지 확인
2. 단조수렴정리를 사용
3. 수렴할 값을 찍어서 수렴 판단
이 때, 급수의 수렴값은 모른다고 봐야 하므로(알면, 굳이 수렴성을 판단해야 하나...?) 1, 2번을 이용하게 된다.
1. 코시수열인지 확인 -> Cauchy Criterion

즉, 부분합이 코시수열인지 확인하면 된다.
이 때, 다음과 같은 성질을 얻을 수 있다.

수렴성으로부터 당연하게 여겼던 바로 그 성질이다...
2. 단조수렴정리를 사용할 수 있는지 확인
(Convergence of Nonnegative Series)
모든 항이 양수인 급수의 경우, 부분합이 단조증가수열이다. 그러므로

(사실 모든 항에 대해서 양수일 필요는 없다! -> 앞에 finite 개수의 항은 어차피 수렴성엔 쓸모 없다!)
위의 1번과 2번을 이용하면 바로 Comparison Test(비교판정법)을 뽑아낼 수 있다. -> 흔히 샌드위치 정리라고 불리는 그것이다.
(Comparison Test)
1. (Convergence Test)
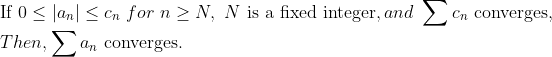
2. (Divergence Test)

(증명)
코시수열임을 증명해보자!
1.
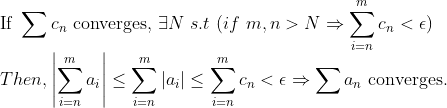
2. 1번의 대우로 생각하자.
만일 c_n이 수렴한다고 가정하면, a_n이 수렴하므로, 2번이 성립한다!
단조수렴정리를 사용해도 상관없지만, 1번의 경우 음수도 포함하기 때문에 제한적이다...
여기서 잠시, 잘 이용하는 몇 가지 급수들을 소개하고 간다.
1. (Geometric Series)

이거야 워낙에 다들 알고 있을거라고 생각해서 자세한 얘기는 생략한다.
2. (예상외로 잘 써먹으면 유용한 급수성질 1)
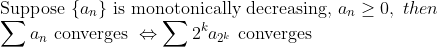
사실, 이건 다음 성질을 증명할 때 쓰였다.

(증명)
단조수렴정리를 이용해보자!
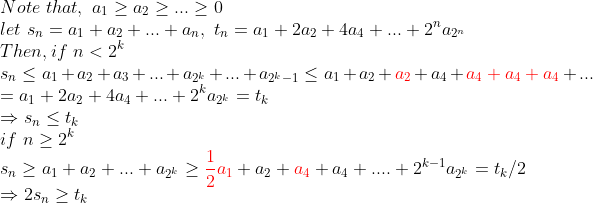
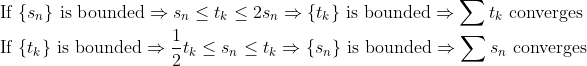
(Note)
1/n에서는 다음과 같이 증명했다.

3. (정수론에서 많이 보는 리만-제타함수 꼴)
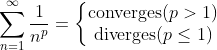
(증명)
위 2번 성질을 이용한다.
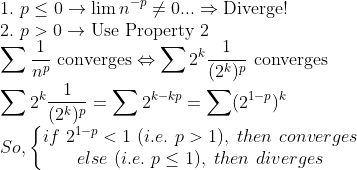
4. (예상외로 잘 써먹으면 유용한 급수성질 2)

사실, 이것도 정수론에서 볼 기회가 많은 것 같다...
(증명)
2번 성질을 이용하면 된다.

미적분학에서 본, root test와 ratio test에 대해서도 똑같이 증명해볼 수 있다!
-> 비교판정법을 보았으므로 음수에 대해서도 상관없이 이용할 수 있다!
(Root Test)
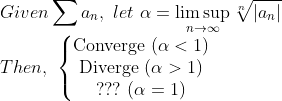
여기서 주목해야 할 건, lim이 아닌, limsup을 이용하였다는 것인데, 이건 별거 아니고, lim 값을 쓰면, 수렴값을 못 구하는 경우가 있어서 limsup으로 대신 사용했다고 생각하면 된다. (수렴하면 lim이나 limsup이나 똑같다. -> 미적분학에서 그냥 lim을 이용하였다는 것을 생각해보자!)
또한, alpha가 1일 때 ???라는 건 판단을 못한다는 뜻이다. (수렴할 때도 있고, 아닐 때도 있고....)
(증명)
(Ratio Test)

어라? Root Test와는 또 다르다....
2번의 ratio가 limsup이 아닌데, 이것이 ratio test가 root test보다 더 안 좋은 이유가 된다.
즉, Root Test가 Ratio Test보다 성능면에서 더 좋다는 것을 알 수 있다!
(물론 계산하기 어려우면, ratio test를 써야 하겠지만...)
(증명)
1.

2. 귀류법으로 접근하자!

위에서 언급한 Root test가 Ratio test보다 더 좋은 이유를 한번 살펴보자.
(Root is Better Than Ratio...)
즉, 다음과 같은 성질을 만족한다. (편의상 양수일 때만 생각해보자.)

(증명)
위의 Ratio Test의 증명을 참고해보자!

infimum의 경우도 같은 방식으로 증명할 수 있다.
(Example)
일반항이 꿀렁거리면서 작아지는 케이스를 한번 보자.

홀수차항과 짝수차항이 커졌다가 작아졌다가 하기 때문에, Ratio Test를 쓰게 되면 1번, 2번 조건 둘 다 걸리지 않게 된다.
하지만, Root test를 사용하게 되면...

위와 같이 수렴하는 것을 확인할 수 있다!!!
여기까지, 급수의 수렴성 테스트인 비교판정법, Root Test, Ratio Test에 대해서 보았다.
미적분학에서 배웠던 Integral Test는 적분을 급수처럼 생각하면 되므로 일단은 패스하고(후에 적분파트에서 다룰수도...?)
다음챕터에선 남은 교대급수와 절대수렴에 대해서 알아보자!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 5-3. 나머지 급수 이야기 (Power Series, Rearrangement) (0) | 2023.02.13 |
|---|---|
| (해석학) 5-2. 시그마(급수)는 막 곱하면 안 되나??? (Convergence of Series 2) (0) | 2023.02.13 |
| (해석학) 4-3. 단조수렴정리와 수열의 수렴값 찾기 (Convergence of Monotonic Sequence) (0) | 2023.02.10 |
| (해석학) 4-2. 수렴하는 점을 꼭 알아야 수렴성을 판단할 수 있나? (Cauchy Sequence) (0) | 2023.02.09 |
| (해석학) 4-1. 지금까지 한 걸 수열에 적용해보자구 (Convergence of Sequence) (0) | 2023.02.09 |




