이번 챕터는 다음과 같은 생각으로 시작한다.
수열 {x_n}이 수렴한다 안한다를 알기 위해서는 어떻게 했었는지 생각해보자... 사실, 수열을 보기만 해도, 대충 이건 수렴하겠지, 발산(혹은 진동)하겠지라고 생각하지 않았는가? 굳이 더 따지자면, 그래프를 그려보면 대....충 나올 거 같으니까, 한 점으로 몰리니까 수렴이다 / 아니다를 판단했었다. 그리고, 더 나아가서 꼭 수렴성을 증명해야 했다면, 수렴하는 점을 그래프를 통해서 알아보고, 그 점으로 수렴하는지 아닌지 판단했었다.
그런데, 앞에서 수렴성 성질에서 수렴 point는 unique하였다. 만약에, 그래프를 보고 대충 이 점에서 수렴하겠지... 했는데 그것보다 약간 옆의 점이 수렴하는 점이라면? 혹은 그래프는 수렴할 것처럼 보였는데, 실제로는 수렴을 하지 않는다면???
-> 사실 모든 점에 대해서 다 수렴하는지 따질 수는 없기 때문에, 수렴하는 점을 먼저 알고 수렴성을 판단하는 것은 꽤나 위험하기도 하고, 논리적으로 맞지도 않다. 수렴하는지 안 하는지도 모르는데, 수렴하는 점이라고 미리 딱 정한다는 게 앞뒤가 바뀌어 보인다...
그러므로, 수렴하는 점을 몰라도, 수렴성을 확인할 수 있는 방법을 알면 좋을 것이다...
이러한 문제를 해결해주는 것이 바로 Cauchy Sequence(코시 수열)이다!
(Cauchy Sequence)(코시 수열)

그러니까, 주어진 epsilon에 대해서, 어떤 N이 넘어가는 두 점 사이의 거리가 모두 epsilon보다 작다는 것을 말해준다.
그냥 보면, 코시 수열은 언제나 수렴할 것 같지만, 그렇지가 않다....
(ex)
{x_n}을 sqrt(2)에 수렴하도록 잡고, 이를 유리수 집합에서 보자....

유리수 집합에서 정의가 되어있다면, sqrt(2)가 유리수집합에 포함되지 않으므로,
이 수열은 분명 코시 수열인데도 불구하고, 수렴하지 않는다.
두 점 사이의 거리가 나왔으니, 집합의 diameter에 관한 개념을 소개한다.
(Diameter of Set)

즉, 가장 먼 두 점 사이의 거리라고 생각해도 무관하다. (물론 Sup!)
또한, A가 코시 수열이라면, n이 커짐에 따라서 diam A_n->0으로 수렴할 것이다. (A_n={x_n,x_{n+1},....})
코시 수열이 수렴하지 않는다는 말이 아쉽지만, 코시 수열은 Compact Set에서 아주 중요한 역할을 한다.
Compact set의 중요한 성질인 축소구간정리와 코시수열이 어떤 연관이 있는지 살펴보자!
(Lemma)

(증명)
(Nested Interval Thm with Cauchy Seq)

(증명)
즉, compact set의 sequence가 코시 수열처럼 행동하면, 축소구간정리와 합쳐져서, 교집합이 nonempty라는 사실과
거기에 더해 오직 1개의 point만 갖는다는 성질을 얻는다. -> 결국에는 수렴하는 point가 된다!
이를 정리하면 다음과 같다.
(Cauchy Sequence and Convergence)
1. 모든 Metric space에 대해서
수렴하는 수열은 코시 수열이다.
2. Compact metric space에 대해서
코시 수열은 수렴한다.
즉, 코시 수열은 수렴한다 <-> 수렴하는 수열은 코시 수열이다.
3. Euclidean Space에서
코시 수열은 수렴한다.
(증명)
1.
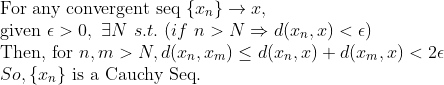
2. 단지, 위의 축소구간정리 성질을 이용했을 뿐이다.
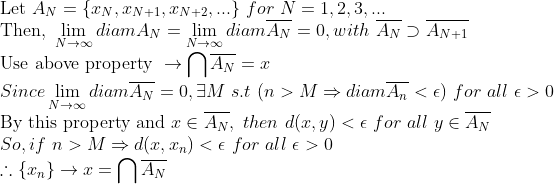
3. Euclidean Space에서의 코시 수열의 경우, 사실 bounded이 된다. 그러므로, 코시수열의 값들을 k-cell로 감쌀 수 있어서, 2번 성질에 의해서 수렴한다.

특히 3번을 증명할 때,
일반적인 compact set의 축소구간정리 -> k-cell이 compact하다(실수의 lub 성질, 완비성 사용) -> 코시수열을 compact set k-cell로 감쌀 수 있다 -> 3번 증명!
그러므로, 결국 3번도 실수의 lub 성질, 즉 실수의 완비성에서 왔다고 할 수 있다.
정리하면, Compact Space에서 Euclidean Space로 올 때, 모두 k-cell이 compact(lub 성질)을 이용하였으므로,
축소구간정리, 코시수열이 수렴, 실수의 완비성(lub 성질)은 모두 동치라는 것이다.
(사실, 세세하게 따지자면, 코시 수열에 아르키메데스 성질이 필요하긴 하다...)
그래서, 우리가 실수의 완비성 파트에서 LUB 성질을 만족하면 Complete Space(Set)이라고 하였었다.
그러므로, 이를 확장하면, metric space X에서 모든 코시 수열이 수렴하면 X를 Complete Space라고 한다.
(Corollary)
모든 Compact set과 Euclidean space는 Complete이다.
여기에 추가로, 위에서 설명했던 것과 같이, complete space에서는 수렴하는 점을 몰라도, 수렴성을 판단할 수 있다.
즉, 주어진 수열이 코시 수열인지만 판단하면, 수렴성은 덤으로 온다.
이렇게 코시 수열인지 판단하는 것을 Cauchy Criterion이라고 한다.
이번 챕터에서는 아주아주 중요한 개념인 Cauchy Sequence에 대해서 다루어 보았는데,
아마 보면서 알겠지만, 결국에 고등학교나 미적분학에서 우리가 계속 놓치고 있었던건
바로, 실수가 무엇인지, 실수의 완비성에 관한 논의였다고 할 수 있다.
물론 이를 위해서 집합과 topology에 대한 내용을 다루긴 했지만, 결론은 실수의 성질에 있었다.
다음 챕터에선 위에서 나온 동치에 + 단조수열의 수렴성을 추가하려고 한다.
즉, 단조수열이 수렴한다는 것을 증명하고, 이 것이 결국 또 실수의 완비성과 동치라는 사실에 대해서 다룰 것이다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 5-1. 급수부턴 수월함.... (Convergence of Series 1) (2) | 2023.02.12 |
|---|---|
| (해석학) 4-3. 단조수렴정리와 수열의 수렴값 찾기 (Convergence of Monotonic Sequence) (0) | 2023.02.10 |
| (해석학) 4-1. 지금까지 한 걸 수열에 적용해보자구 (Convergence of Sequence) (0) | 2023.02.09 |
| (해석학) Summary 1. 지금까지의 내용을 정리해보자! (Summary of Basic Set & Topology) (0) | 2023.02.09 |
| (해석학) 3-3. Compact set이면 다 k-cell처럼 생겼을까? (Cantor Set) (0) | 2023.02.07 |





