지난 챕터에 이어서, 이번에는 단조유계수열의 수렴성에 대해서 살펴보자.
먼저, 단조수열의 정의부터 보자.
(Monotonic Sequence(단조수열)) -> 당연히 실수열일 것이다.
1. Monotonically Increasing(단조증가수열)

-(Strictly) Monotonically Increasing

2. Monotonically Decreasing(단조감소수열)

-(Strictly) Monotonically Decreasing

그러면, 이번에도 이 단조수열에 LUB 성질을 이용해보자
(Monotonic Convergence Theorem)(단조수렴정리)

즉, 단조수열에 대해서 유계이면 수렴하고, 수렴하면 유계이다.
(증명)
1. 수렴 -> 유계 : 일반적인 수열로 앞에서 이미 다루었다!
2. 유계 -> 수렴 : 실수의 완비성을 이용하자.

자, 이번에도 이용한건 단지 실수의 LUB 성질(완비성)뿐이다.
정리하면, 실수에서 LUB 성질, 축소구간정리, 코시수열의 수렴, 단조수렴정리, 하이네-보렐 정리, 볼차노-바이어슈트라스 정리 모두 동치이다.
이번에는 수열이 수렴하지 않더라도, 값이 어떻게 변화하는지에 관한 이야기를 해보려고 한다.
정확히 말해서, 수열이 수렴하는지 안하는지는 관심이 없고, n이 커짐에 따라서 수열이 어디로 가는지 그 최댓값과 최솟값을 알고 싶은 것이다.
예를 들어서 x_n=(-1)^n이라는 수열은 분명히 수렴하지 않지만, n이 커짐에 따라서 기껏해야 -1<=x_n<=1일 것이다.
이미, 우리는 최댓값과 최솟값 대신에 좋은 tool인 sup, inf를 알고 있다.
그러므로, 수열의 upper limit와 lower limit를 다음과 같이 정의하자.
(Upper(Lower) Limit of Sequence)

처음 본다면 당황할 수도 있는데, 이렇게 생각해보자.
upper limit의 경우, x_n의 모든 subsequence의 수렴값들 중 sup(최댓값)을 뽑았다고 생각하면 된다.
위의 예시를 생각해보면 (x_n=(-1)^n)
부분수열을 1, 1, 1, 1, .....로 뽑을 수 있으니, limsup x_n = 1이 될 것이다.
반대의 경우도 liminf x_n=-1이 될 것이다.
사실, x_1,x_2,....같은 수열 앞쪽의 경우, 수렴값에 전혀 영향을 주지 못한다는 점을 생각하면(수렴 정의를 생각해보자!)
upper limit와 lower limit의 표현을 왜 limsup, liminf로 했는지 알 수 있다...
-> 결국 n이 클 때의 x_n의 움직임에 따라서 부분수열의 수렴값들이 결정나기 때문!!
또한, 다음과 같은 성질은 Trivial하다...
(Convergence and Upper(Lower) Limit of Sequence)

수열의 upper limit과 lower limit에 관한 성질들은 다음과 같다.
(Upper(Lower) limit of seq -> properties...)

(증명)
1.
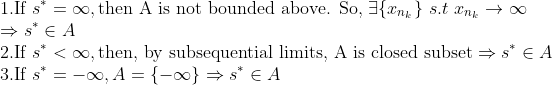
두번째에서, 부분수열의 성질을 이용하였다.(부분수열의 수렴값들의 set은 closed set)
2. 대우를 이용하였다.

2번에서 중요한 것은 오히려 대우이다.
즉, upper limit에서 저런 N을 잡을 수 없다면(즉, finite 개수의 항만 a보다 작다면) a가 s*보다 작거나 같다.
(Corollary)

그리고 아주 trivial하게, 다음과 같은 성질도 얻을 수 있을 것이다.

아주 간단한 성질이지만, 이를 이용해서 수열과 급수의 수렴성, 특히 비교판정법(Comparison Test)의 기초가 되므로, 중요한 성질이다. -> 미적분학의 비교판정법 참고!
(미적분학) 2-1. 입실론-델타논법으로 수렴성 증명은 귀찮아 (Comparison Test, Ratio Test, Root Test, Integral Test) : https://0418cshyun.tistory.com/4
(미적분학) 2-1. 입실론-델타논법으로 수렴성 증명은 귀찮아 (Comparison Test, Ratio Test, Root Test, Integral
(해석학 참고링크) -최소상계/최대하계(sup, inf)- (해석학) 1-1. 도대체 뭐가 문제라 증명을 못했을까? (What is Real Number?) : https://0418cshyun.tistory.com/14 (해석학) 1-1. 도대체 뭐가 문제라 증명을 못했을까
0418cshyun.tistory.com
단조수렴정리를 이용해서 얻을 수 있는 몇가지 공식들을 적어본다면
(Formulas for Convergence Test)

증명을 다 하지는 않겠지만, 예를 들어서 2번을 증명해보면
1. p>1인 경우
a. 일단, 수렴하는지 체크해야 한다. -> by 단조수렴정리
-> 일반항이 단조감소수열이고, 항상 1보다 크거나 같으므로 bounded -> 수렴한다.
b. 수렴값이 얼마인지 찾아보자.
-> 수렴한다는 것은 알고 있으므로 다음과 같이 표현할 수 있다! (lim값이 존재한다.)
-> (즉, 수렴하는지 모르면 이 표현을 쓰면 안된다.)

a<1은 일단 불가능하다. 왜냐면, 일반항이 항상 1보다 크거나 같으므로,

또한, a>1인 것도 불가능하다. 왜냐면, a가 1보다 크면, a보다 큰 항이 finite 개수일 것이기 때문이다. (위의 upper/lower limit of seq 성질 2번을 위반한다. -> lower limit인 경우로 생각해보자!)
그러므로, a=1이다.
2. p=1인 경우 -> 자명
3. 0<p<1인 경우

그러므로 2번을 증명하였다.
3번의 경우
a. 먼저 수렴하는지 체크하자 -> by 단조수렴정리
그런데, 이 수열이 단조수열인지 체크하는게 조금 까다롭다... 평균값정리를 쓰자!

그러므로 일반항이 단조감소수열이다. (n>2인 경우...) 사실, finite개수의 항은 수렴성을 따질 때 무시할 수 있을 것이다.(어차피 수렴성에 영향 안 준다.) 그러므로, 그냥 똑같이 생각할 수 있다!
또,

이므로, 주어진 수열은 bounded이다.
그러므로 주어진 수열은 수렴한다. 즉,

b. 수렴값을 찾아보자
-> 이건 2번과 똑같이 하면 되므로, 굳이 적지는 않겠다. (단조감소임을 이용하면 편하다!)
위의 flow대로하면 위에 나온 공식의 극한값을 구할 수 있다.
특히, 4번의 경우 분자 -> Polynomial(다항함수), 분모 -> Exponential(지수함수) 라는 것을 생각하면
지수함수가 다항함수보다 미친듯이 빠르게 증가한다는 것을 알 수 있다.
여기까지 수열의 수렴성에 관한 내용을 마무리한다.
정리하자면, 수열에서 수렴성을 체크하기 위해선
1. 수렴값이 될 거 같은 거 하나 찍고, 수렴성을 체크 -> 수렴하면 좋지만, 수렴 안하면 다른 값들 다 넣어봐야 함.... -> BAD지만 가장 쉽게 쓸 수 있음
2. 코시 수열인가? -> 급수에서 많이 활용
3. 단조유계수열인가? -> 급수에서 많이 활용
이 정도의 방법이 있다.
다음 챕터에서는 급수의 수렴성에 관해서 이야기할 것인데, 새로운 건 없고, 수열의 수렴성과 거의 동일하다. 다만, 수렴성 테스트에 조금 더 집중을 하기 때문에, 미적분학 카테고리의 급수의 수렴성 테스트를 참고하면 좋다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 5-2. 시그마(급수)는 막 곱하면 안 되나??? (Convergence of Series 2) (0) | 2023.02.13 |
|---|---|
| (해석학) 5-1. 급수부턴 수월함.... (Convergence of Series 1) (2) | 2023.02.12 |
| (해석학) 4-2. 수렴하는 점을 꼭 알아야 수렴성을 판단할 수 있나? (Cauchy Sequence) (0) | 2023.02.09 |
| (해석학) 4-1. 지금까지 한 걸 수열에 적용해보자구 (Convergence of Sequence) (0) | 2023.02.09 |
| (해석학) Summary 1. 지금까지의 내용을 정리해보자! (Summary of Basic Set & Topology) (0) | 2023.02.09 |



