(미적분학 참고링크)
-교대급수, 절대수렴-
(미적분학) 2-2. 음수항이 있는 급수는 어떻게 하지? (Alternating Series Test, Absolute Convergence) : https://0418cshyun.tistory.com/5
(미적분학) 2-2. 음수항이 있는 급수는 어떻게 하지? (Alternating Series Test, Absolute Convergence)
앞 챕터에서 양수항을 가지는 급수만을 다루었다면 이번 챕터에서는 음수항을 가지는 급수에 대해서도 다뤄볼 것이다. 1. (Alternating Series)(교대급수) 급수의 일반항의 부호가 계속 교대로 나오는
0418cshyun.tistory.com
이번 챕터에서는 저번시간에 말했던 것처럼, 교대급수(Alternating Series)와 절대수렴(Absolute convergence)에 관하여 다룰 것이다.
먼저, 교대급수(alternating serires)란 부호가 반복적으로 바뀌는 급수를 말한다. (+,-,+,-,+,-,......)
그런데, 이 교대급수는 다음과 같은 급수의 곱(? -> 뒤에 이유가 나온다.)으로 생각할 수 있다.
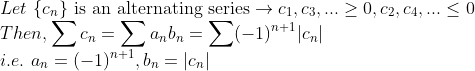
여기서 당연히 다음을 알 수 있다...

여기서는 조금 더 일반화된 논의를 위해서 교대급수 대신에 급수의 곱의 수렴성에 대해서 알아본다.
먼저, 급수의 곱의 수렴성에서 자주 쓰이는 식을 소개한다.
(Partial Sum Formula)
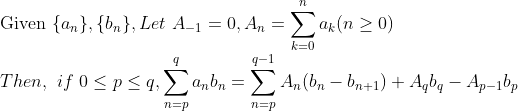
주어진 두 급수의 곱을 Partial sum과 수열의 차로 분리를 한 것인데, 대부분의 경우
Partial sum -> bounded로 처리가능, 수열의 차 -> 대부분 수렴하는 경우일 때 사용하므로 0으로... -> 수렴성 확인 가능!
이므로, 잊어버릴 때 쯤 되면 간혹가다 나오는 것 같다...
(증명)
사실, 증명이라고 할 것도 없는게, 수식 풀어서 쓰면 된다...
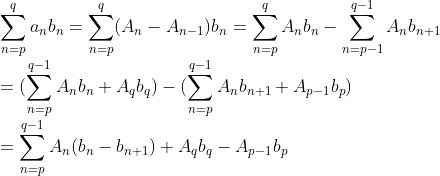
위에서도 간략히 소개했지만, 위의 성질을 이용해서 다음과 같은 일반적인 성질을 얻는다.
(Convergence of Multiplication of General Terms...)
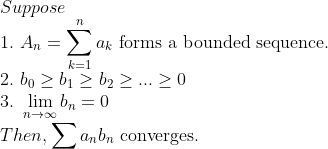
(증명)
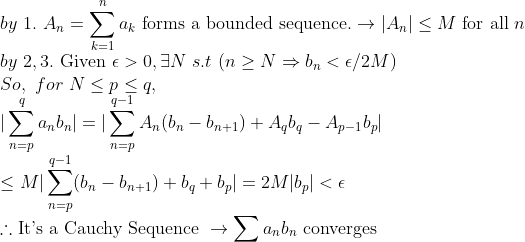
이런 증명방법은, 후에 적분할 때 많이 등장하므로 알고 있으면 유용하다.
(Corollary) (Convergence of Alternating Series)
다음과 같은 교대급수는 수렴한다.
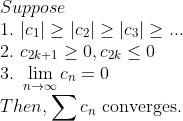
(증명)
위의 성질을 쓰면 간단하게 증명된다. -> 급수의 곱의 수렴성에서 각 조건을 확인해보자!
1. |Partial sum|은 c_1보다 항상 작거나 같다! -> bounded
2,3. 나머지는 Trivial!
다음으로, 절대수렴(Absolute Convergence)에 대해서 알아보자.
(Absolutely Convergent)(절대수렴)
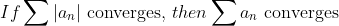
(증명)
코시수열임을 보이자.
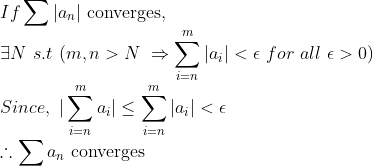
사실, 저 꼴로도 쓸 수 있겠지만, 보다 정확히는
-> 양수인 수열의 급수가 수렴하면 그 수열에 마이너스를 마음대로 붙인 급수도 수렴한다
로 생각하면 좋다.
절대수렴을 바탕으로, 보다 더 강력한 급수의 곱 성질을 얻을 수도 있는데,

그런데, 이를 절대수렴을 이용하면, 이와 뭔가 비슷한 꼴로 만들어서 수렴성을 보일 수 있다.
(Convergence of Product of Series)
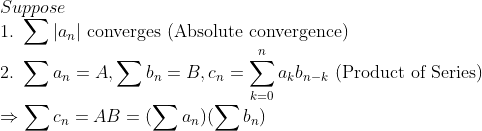
즉, 두 급수 다 수렴을 하는데, 한쪽이 절대수렴이면 급수의 곱이 수렴한다는 것이다!!!
(물론, 위에서 본 곱과는 차이가 있다! -> 여기서 나온 c_n을 일반적으로 급수의 곱이라고 얘기한다.)
(증명)
억지로 C=AB+... 꼴을 만들어 준 다음에 ...이 0으로 수렴한다는 것을 보인다.
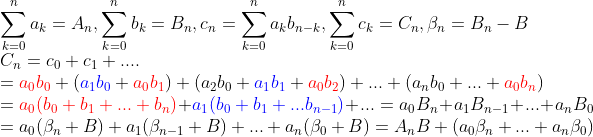
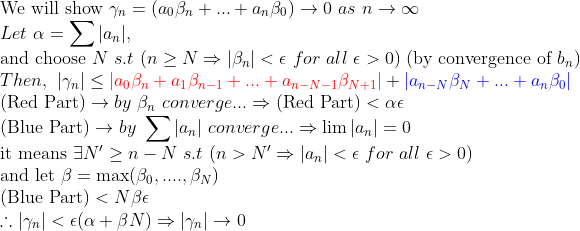
특히, 여기서 저렇게 part를 나누어서 한쪽은 a_n의 수렴성을 이용하고, 다른 쪽은 beta_n의 수렴성을 이용하는 방법은 아주 많이 나오므로(특히 곱에서) 꼭 알아두자!
여기까지 (교대급수와 절대급수 -> 사실은 급수의 곱의 수렴성) 에 관해서 다루어 보았다.
다음시간에는 분량 때문에 얘기를 못했던, Power series(멱급수)와 Rearrangement(재배열)에 관해서 다루어 볼 것이다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 6-1. 드디어 함수의 극한과 연속... (Limit and Continuity of Function) (0) | 2023.02.14 |
|---|---|
| (해석학) 5-3. 나머지 급수 이야기 (Power Series, Rearrangement) (0) | 2023.02.13 |
| (해석학) 5-1. 급수부턴 수월함.... (Convergence of Series 1) (2) | 2023.02.12 |
| (해석학) 4-3. 단조수렴정리와 수열의 수렴값 찾기 (Convergence of Monotonic Sequence) (0) | 2023.02.10 |
| (해석학) 4-2. 수렴하는 점을 꼭 알아야 수렴성을 판단할 수 있나? (Cauchy Sequence) (0) | 2023.02.09 |



