(미적분학 참고링크)
(미적분학) 1. 왜 미적분하는데 수열과 급수를 배우는거지? (입실론-델타 논법) : https://0418cshyun.tistory.com/3
(미적분학) 1. 왜 미적분하는데 수열과 급수를 배우는거지? (입실론-델타 논법)
(해석학 참고링크) -수열의 수렴성- (해석학) 4-1. 지금까지 한 걸 수열에 적용해보자구 (Convergence of Sequence): https://0418cshyun.tistory.com/50 (해석학) 4-1. 지금까지 한 걸 수열에 적용해보자구 (Convergence o
0418cshyun.tistory.com
이번 챕터에서는 이제까지 배웠던 set, topology 내용들을 수열에 적용시켜볼 것이다.
먼저, 수열(Sequence)의 정의는 앞에서 잠깐 나왔던 것처럼,
(Sequence(수열))
자연수집합을 정의역으로 갖는 함수. 즉, 다음을 그냥 수열이라고 부른다.

(Convergence of Sequence(수열의 수렴))

이미, 다 알고 있는 내용들이지만, 여기서 하나 체크하고 넘어가야 할 건, 수렴하는 x가 X에 존재해야 한다는 것이다.
예를 들어서

또한, x_n이 수렴하지 않으면 발산(diverge)한다고 한다.
(NOTE) -> 증명할 때 따로 언급하지 않을 거에요!
위에서

이렇게 바뀌어도 전혀 상관이 없다. 만일, "epsilon보다 작거나 같다" 로 바뀌면, 그것보다 아주 약간 작은 epsilon1을 다시 잡으면 "epsilon1보다 작거나 같다" ->"epsilon보다 작다" 조건을 만족시킬 수 있기 때문이다.
같은 논리로

상수배 붙인 걸로 바뀌어도 전혀 상관이 없다.
만일 m*epsilon으로 바뀌면 다시 epsilon을 잡을 때, (epsilon/m)으로 잡으면 똑같이 epsilon보다 작다라는 표현을 만족시킬 수 있기 때문이다.
(Convergence and Limit Point)
수렴의 정의를 보면 뭔가 limit point의 정의와 부합하는 느낌이 들 것이다.
일단, {x_n}이 x에 수렴하면, x는 {x_n}의 limit point임은 자명하다. 왜냐하면, 어떤 반지름으로 open ball을 잡아도, 그 안에 {x_n}의 원소가 있기 때문이다.
그런데, x가 {x_n}의 limit point라고 해서, {x_n}이 x에 수렴하지는 않는다.

예를 들어서,

왜냐하면, 수렴성 정의에선, 어떤 n보다 크면 open ball에 다 들어가야 한다는, 즉, 겹치는 원소에 대한 제약이 있는 반면,
limit point는 그런 n에 대한 제약이 없기 때문이다.
굳이 따지자면, 다음 그림처럼 표현할 수 있을 것이다.

또한, limit point와 수렴성을 그림으로 표현하면 다음과 같다.
1. LIMIT POINT

2. Convergence of Seq

이 경우에, 주어진 epsilon은 원의 반지름이 될 것이고, n>=12=N이면, 주어진 open ball에 다 들어간다...(물론 20개만 표현하였지만) 모든 epsilon에 대해서, 이런 N이 있다면, 수렴할 것이다...
위에 나온 얘기에서 조금 더 들어가면 다음과 같은 성질을 얻는다.
1. (Uniqueness of Convergence)
만일, 수열 {x_n}이 x와 x'로 수렴한다면, x=x'이다.
즉, 주어진 수열에서 수렴하는 point는 기껏해야 1개이다.
2. (Bounded Sequence)
만일, 수열 {x_n}이 수렴한다면, {x_n}은 유계이다.(bounded)
3. (Existence of Convergent Sequence from a limit point)
만일 x가 A의 limit point라면, x로 수렴하는 {x_n}을 A에서 잡을 수 있다.
-> 앞에서 본 limit point와 convergence 관계의 역이다!!!
(증명)
1.

위에서 epsilon을 아무거나 잡아도, 주어진 x,x'의 거리는 2epsilon보다 작아야 하므로, 거리는 0이 될 수밖에 없다.
2.
{x_n}이 x로 수렴한다고 하면(x는 unique!), 어떻게 반지름을 잡아도, infinite 개수의 항이 open ball에 들어가게 된다.
그러므로, open ball 밖에 남아있는건, finite 개수의 항밖에 없고, 그 finite 개수 항 중, x에서 가장 먼 항을 x'라고 잡으면, {x_n}은 중심이 x이고, 반지름이 d(x,x')인 open ball에 다 들어간다. 그러므로, {x_n}은 유계이다.
-> compact set의 예시를 생각해보자!
3.
x로 수렴하는 {x_n}을 A에서 한번 구성해보자!
일단, A가 limit point x를 가지므로, A는 infinite set이다.
그러면 중심이 x이고 반지름이 1인 open ball에서 A의 원소를 하나 잡아서 x_1이라고 하자. (단, x는 제외)
또, 반지름이 1/2인 open ball에서 A의 원소를 또 잡아서 x_2라고 하자... -> 반복....
그러면, 이렇게 구성된 {x_n}이 x로 수렴하는지 보자.

그러므로, {x_n}은 x로 수렴한다.
위에서 수렴하는 수열이 유계이고, 또 수렴성과 limit point가 연관이 되어있다는 것을 생각하면,
하이네-보렐 정리에 따라서, 닫힌 유계집합 -> compact set이 연관이 되어 있다는 것을 생각해볼 수 있다. (물론, Euclidean Space에서...)
이 논의를 하기 위해서 subsequence(부분수열)에 관해서 잠시 알아보자.
(Subsequence(부분수열))

즉, subsequence는 주어진 수열에서 순서에 맞추어 하나씩 임의로 뽑아서 만든 수열이라고 생각하면 된다.
그렇다면, 다음 성질은 당연하게 성립한다.

증명은 워낙에 trivial해서, 생략한다.
그럼 여기서 compact set과 어떤 관련이 있는지 살펴보자.
1. (Compact set and Convergence of Subseq)
만약 {x_n}이 compact metric space X에서 정의되어 있다면, X의 point에 수렴하는 부분수열{x_nk}를 잡을 수 있다.
2. (Bounded and Convergence of Subseq)
유클리드 공간의 모든 유계인 수열은 수렴하는 부분수열을 가진다.
3. (Closed set and Convergence of Subseq)
만약 {x_n}이 metric space X에서 정의되어 있고, 부분수열의 수렴값들로 이루어진 set을 A라고 한다면,
A는 X의 closed subset이다.
(증명)
1.

2. 유클리드 공간의 유계인 수열은 k-cell(compact set)로 덮일 수 있으므로 1에 의해 수렴하는 부분수열을 가진다.
3.
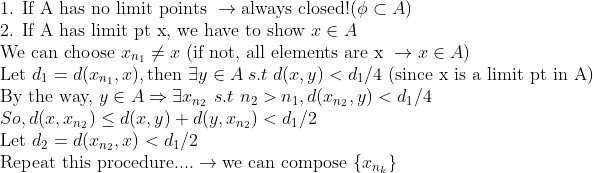
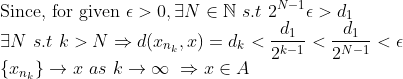
보충해서 설명하자면, 1번의 경우 limit point가 없다면, 당연히 A는 closed set이고,
2번의 경우, limit point가 x라고 하면, 원래 수열에서 x가 아닌 원소 하나(x_n1)를 가져온다.
이 때, x는 A의 limit point라서, 근처에 A의 원소 y를 가지고 있다.
또한, y는 부분수열의 수렴값이니, 그 부분수열에서 x_n2를 위의 조건에 맞게 고를 수 있다.
그럼, metric의 성질에 의해서 x와 x_n2의 거리가 x와 x_n1의 거리의 반보다 작다는 것을 알 수 있다.
이를 반복하면서 x_n3, x_n4,....를 구해서 부분수열을 만든다.
이 부분수열이 x에 수렴하므로, x는 A의 원소이다. -> closed set이다.
여기까지, 수열의 수렴성과 위상적 성질을 일차적으로 알아보았다.
사실, 정의를 제외하고, 이 성질들을 잘 쓴다기 보단, 후에 증명에서 이런 성질들을 약간씩 꺼내 써야 하기도 하고, 증명방법을 알아두면 편하기 때문에 본다고 생각하면 된다.
앞에서 open/close/compact 등의 성질을 잘 이해한다면, 오히려 이 부분이 직관적으로 느껴질 수도 있긴 하다.
다음에는 중요한 Cauchy Sequence에 대한 내용과 이에 관련된 실수의 완비성에 관한 내용을 다룰 것이다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 4-3. 단조수렴정리와 수열의 수렴값 찾기 (Convergence of Monotonic Sequence) (0) | 2023.02.10 |
|---|---|
| (해석학) 4-2. 수렴하는 점을 꼭 알아야 수렴성을 판단할 수 있나? (Cauchy Sequence) (0) | 2023.02.09 |
| (해석학) Summary 1. 지금까지의 내용을 정리해보자! (Summary of Basic Set & Topology) (0) | 2023.02.09 |
| (해석학) 3-3. Compact set이면 다 k-cell처럼 생겼을까? (Cantor Set) (0) | 2023.02.07 |
| (해석학) 3-2. Compact set의 중요한 성질들 (축소구간정리, 하이네-보렐 정리, 볼차노-바이어슈트라스 정리) (0) | 2023.02.06 |



