(해석학 참고링크)
-수열의 수렴성-
(해석학) 4-1. 지금까지 한 걸 수열에 적용해보자구 (Convergence of Sequence): https://0418cshyun.tistory.com/50
(해석학) 4-1. 지금까지 한 걸 수열에 적용해보자구 (Convergence of Sequence)
(미적분학 참고링크) (미적분학) 1. 왜 미적분하는데 수열과 급수를 배우는거지? (입실론-델타 논법) : https://0418cshyun.tistory.com/3 이번 챕터에서는 이제까지 배웠던 set, topology 내용들을 수열에 적용
0418cshyun.tistory.com
고등학교때 미적분을 배우면 알겠지만 그냥 커리큘럼대로 흘러서 배우다 보면 수열/급수와 미적분이 별로 연관성이 없어보이지만, 사실 고등학교 때 수열/급수를 배우면서 뭔가 자연스럽게 흘러가듯이 중요한 포인트를 놓치고 넘어갔을지도 모른다.
일단 결론만 말하자면, 수열과 급수를 배우는 목적은 거의 "Limit(극한)"에 있다!
일단 대부분의 고등학생들이 아는 미분의 정의는 다음과 같은데

고등학교 과정에서는 일단 이 "limit"이 뭔지 수렴, 발산이 뭔지 제대로 설명하지 않는다. (물론, 해석학 내용을 보면 그럴만하다고 생각할수도 있다.)
그래서 이 Limit를 정의하는 과정이 필요한데, 이를 입실론-델타 논법을 이용하여 정의한다.
먼저 수열(Sequence)에 대해 살펴보자.
(수열의 수렴(Convergence of Sequence))
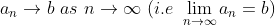
(수열 a_n이 b로 수렴한다)는 다음을 뜻한다.

만일 이 수열이 어느 수에도 수렴을 하지 않는다면 이 수열은 발산(Diverge)한다고 한다.
(여기서 epsilon은 실수, n, N은 자연수)
처음 보는 사람들은 이게 뭐야?? 라고 할만한 영어와 수식이 등장하는데, 천천히 하나씩 살펴보자.
먼저, 사람들이 많이 실수하는 표현 For all에 대해서 살펴보자.
단순하게 "For all X>0" 이라고 하면 "모든 X>0에 대해서" 라고 해석하기 쉬운데 이렇게 생각하면 추후에 나오는 모든 입실론-델타 논법에서 헷갈릴 여지를 아~~~~주 많이 남기기 때문에 다음과 같이 생각하는 것이 이롭다.
For all X>0 -> Given X>0 (주어진 X>0에 대해)
주어진 X에 대해??? -> 어차피 어떻게 X를 줄지는 모르니까 결국엔 모든 X에 대해서라는 말과 동일하다!
다시 문제로 돌아와서
저 수열이 b에 수렴한다는 뜻은
모든 epsilon에 대해서 어떤 자연수(N)가 존재하는데, 이 N은 "N보다 큰 모든 자연수 n에 대해서 수열 a_n과 b 사이의 거리(위 식에서 세로 두 줄은 거리(Norm)을 뜻함)가 epsilon보다 작다" 라는 것을 만족해야 한다.
한국어로 적었지만 역시나 이해하기는 어려워보인다.
예를 하나 들어보자.

당연히 이 수열은 n이 무한대로 갈때, b=0으로 수렴한다. (고등학교 수학을 배웠다면 자명하겠죠??)
일단, epsilon=1/10으로 찍어보자. (Given epsilon)
그럼 N=10이라면, n>10인 모든 n (n=11,12,....)에 대해서 a_n과 b 사이의 거리가 1/10보다 작으므로 위 조건을 만족한다.
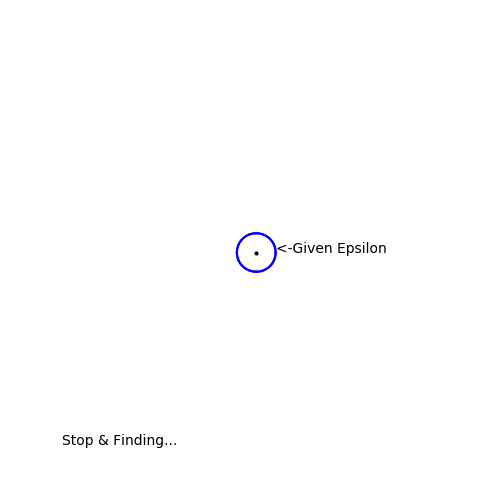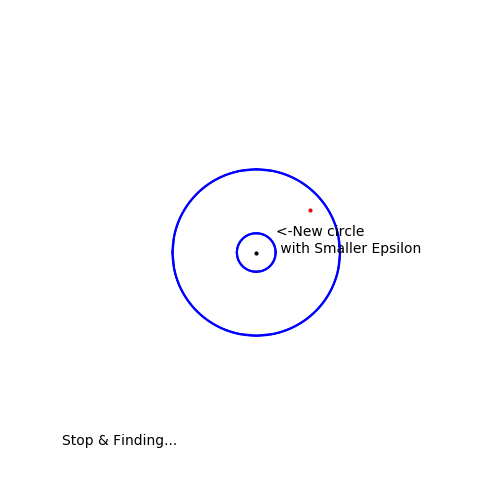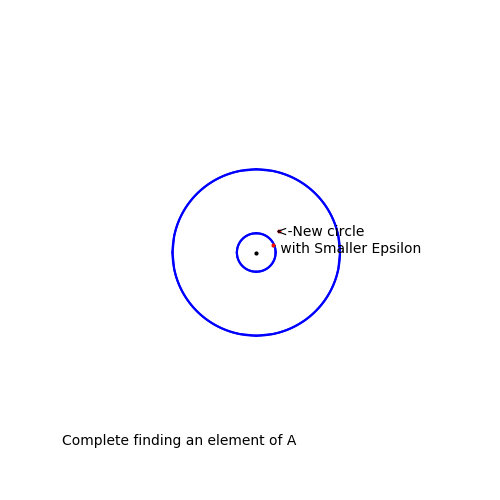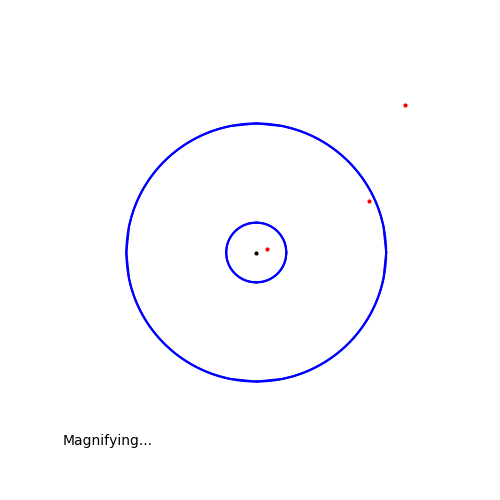
다음으론, epsilon = 1/1000으로 찍어보자
그렇다면, N=1000이면 같은 이유로 위의 조건을 만족한다.
이런식이라면 epsilon을 어떻게 잡아도(For given epsilon) N이 충분히 크면 위 조건을 만족할 것이다.
물론 증명을 할 수도 있다!
(증명)

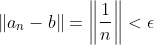
(여기서 [ ]는 가우스 기호를 뜻한다.([2.4]=2, [-3.14]=-4))
입실론-델타 논법이란건 결국 이런식으로 극한을 정의하는 방법이라고 설명할 수 있고, 나중에 함수의 극한도 이와 유사한 방법으로 (그때는 델타도 같이 써서) 정의한다.
또한, 극한을 이용한 성질들(특히, 연속....)도 입실론-델타 논법을 이용해서 정의하게 된다.
급수(Series)도 부분합을 이용하면 수열과 똑같이 생각할 수 있다!
(급수의 수렴(Convergence of Series))
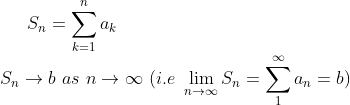
(급수 S_n이 b로 수렴한다)는 다음을 뜻한다.

만일 이 급수가 어느 수에도 수렴을 하지 않는다면 이 급수는 발산(Diverge)한다고 한다.
(여기서 epsilon은 실수, n, N은 자연수)
그런데....
이런식으로 정의하고, 증명하는게 뭔가 장점이 있나??? 라는 생각이 들면 꽤 잘 따라오는 것이다.
사실 어떻게 보면 고등학교 때 했던 방식이 더 직관적이고 간단해보인다. 그러나 '그래프 개형 보니까 그냥 그럴거 같아요... '하는 논리로는 복잡한 수열이나 함수의 수렴성을 정의하기 상당히 어렵다. (ex. 소수정리의 엄밀한 증명)
이러한 논의의 필요성은 여기서 다루려고 하는 미적분학의 내용을 훨씬 넘어가므로 더이상 다루지 않고 해석학을 참고하기 바란다.
일단 입실론-델타 논법을 맛보기로 보긴 했는데, 위의 수열의 수렴성 증명처럼 매번 하려면 사실 많이 귀찮은게 사실이다.
그래서 다음 챕터에서 빠르고 더 쉽게 수열/급수의 수렴성을 판단하는 방법을 소개한다.


