일단 이 챕터를 시작하기 전에 테일러 급수에 대해서 알고 들어가자.
일단 여기서 테일러 급수는 어떤 함수 f(x)를 다항함수(Polynomial)꼴로 표현하는 방법이라고 생각하면 된다. 예를 들어 exp(x)나 sin(x)등의 함수를 다항함수 꼴로 표현하는 것이다.
(NOTE) 나중에 푸리에 급수를 보게 될 일이 있다면 푸리에 급수는 f(x)를 sin, cos의 삼각함수 형태로 표현하는 방법이라고 생각하면 된다.
그런데 아무 f(x)나 다항함수 꼴로 표현할 수는 없다. 정확히 말해서 테일러 급수 형태로 표현은 가능한데 이렇게 만든 급수가 원래 f(x)를 따라가지 않는 경우가 생긴다. 즉, 원래 함수와 테일러 급수의 오차가 너무 나게 된다.....
그래서 이 오차를 측정해서 테일러 급수를 써도 되는지 안되는지 체크하는 방법이 테일러 정리가 된다.
(Taylor Theorem)
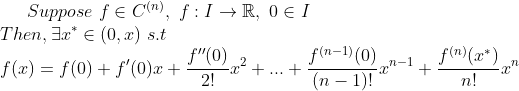
테일러 정리를 이해하는건 일단 뒤로 미루고 테일러 급수의 중요성에 대해서 잠시 언급하자면
실제로 다루는 함수들은 대부분 초월함수(삼각함수, 지수함수, 로그함수 etc...)가 많은데, 테일러 급수는 이를 다항함수로 취급할 수 있도록 만든다. 다항함수를 이용하면 미분과 적분이 편하고 다항함수의 다양한 성질들은 직관적이기도 하고 쓰기도 편하기 때문에 테일러 급수는 중요하다고 할 수 있다. 게다가 테일러 급수가 요구하는건 "n번 미분가능하다"라는 조건인데 대부분의 함수들이 이를 만족하기 때문에 사용범위도 꽤 넓다.
이번 챕터에선 이 테일러 급수의 기초가 되는 Power Series에 대해서 설명을 한다.
(Power Series)

단지 급수에 다항함수항이 붙은 것뿐이다. 그러므로 수렴확인도 앞에서 본 급수의 수렴판정을 그대로 이용하면 된다.
(Convergence of Power Series) -> Root Test를 이용하던지 Ratio Test를 이용하던지 상관은 없지만, Ratio Test가 더 엄격하고 부호에서도 자유로워 이 챕터에서는 Ratio Test를 중심으로 전개한다.
(Ratio Test)

즉, |x|가 수렴반경(convergence radius)보다 작은 지점에서 power series는 수렴
|x|가 수렴반경보다 큰 지점에서는 power series가 발산한다.
다만 이때에도 |x|=수렴반경 인 경우에는 이를 통해서 확인할 수 없으므로 다른 방법을 이용해서 수렴성을 체크해야 한다.
또한, 테일러 급수에서 보았듯이 power series와 미분과의 관계성이 필요한데, 이는 다음으로 설명 가능하다.
참고로 아직은 power series를 그냥 막 미분이나 적분을 해서는 안된다. (물론 결과론적으론 해도 된다.)
왜냐면 (무한합의 미분) = (각 항의 미분의 무한합) 인지는 아직 증명하지 않았기 때문이다!
이를 보이기 전에 일단 꺼림칙한 수렴성 여부에 대해서 살펴본다.
(Convergence of Differentiation, Integration of Power Series)

즉, 원래의 power series가 수렴하는 x에서는 미분이나 적분을 해도 그 x 범위에서는 수렴성을 보장한다는 내용이다.
이 정리는 위의 ratio test로 보일 수 있으니 생략한다.
그래서 결론적으로 우리가 원하는 것은
(Differentiation, Integration of Power Series)
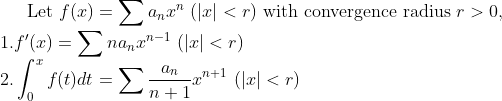
즉, 위에서 얘기했던 f(x)의 미분과 적분은 각 항을 미적분한 것의 무한합과 동일하다 라는 내용이다.
(증명)
(1)
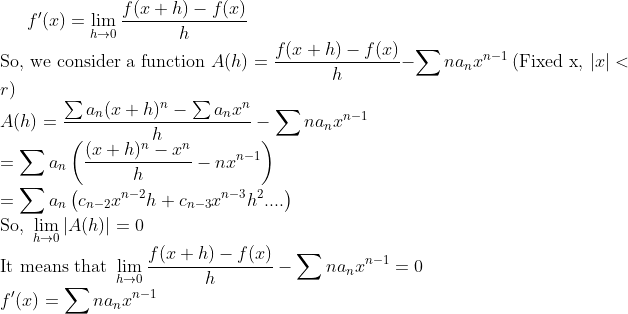
중간에 괄호 안을 계산해보면 x^n, x^(n-1) 항이 사라지면서 h에 관한 상수항이 다 사라지면서 lim을 취하면 0으로 보낼 수 있다.
(2)의 경우 (1)과 미적분학의 기본정리를 거꾸로 적용하면 바로 구할 수 있다.
즉, 여기서 알 수 있는건 수렴반경 안에서는 power series의 미분과 적분을 마음대로 해도 된다라는 것이다.
다음 챕터에서는 이번 챕터에서 살짝 넘어가버렸던, 함수의 극한과 미분에 대해서 다뤄 볼 것이다.



