(미적분학) 3-2. 근데 우리가 필요한건 수열보단 함수 아니었나?? (Convergence, Continuity of function)

(해석학 참고링크)

 

-함수의 극한과 연속-

(해석학) 6-1. 드디어 함수의 극한과 연속... (Limit and Continuity of Function) : https://0418cshyun.tistory.com/57

(해석학) 6-1. 드디어 함수의 극한과 연속... (Limit and Continuity of Function)

 

미적분학에서 사실 실제로 미적분에 이용할 것은 수열이 아니라 함수이다.

 

저번 챕터까지는 수열의 극한에 대해서 살펴보았고, 이번 챕터에서는 함수의 극한과 연속에 대해서 살펴보자.

함수의 극한도 입실론-델타 논법을 이용하여 정의한다.

---

(함수의 극한)

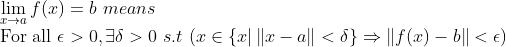
이번에는 delta까지 등장하면서 또 머리를 어지럽게 한다....

이번에도 하나씩 천천히 살펴보자.

수열의 극한에서 처럼 For all은 Given으로 해석해서 생각하면 된다.

다음으로 () 안의 조건을 만족하는 delta가 존재하면 f(x)의 극한값은 존재한다.

()안의 조건을 살펴보면 다음과 같다.

a 근처의 모든 x(거리가 delta보다 작은 모든 x)에 대해 함수 f로 mapping하면 각 f(x)는 b 근방(거리가 epsilon보다 작은 지점에) 존재한다 라는 뜻이다.

 

이해가 안 간다면, 이번에도 예시를 하나 들어보면서 생각해보자.

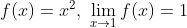
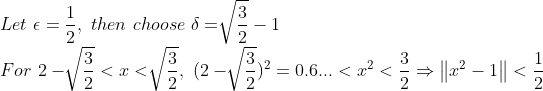
이런식으로 각 epsilon에 따라서 delta를 임의적으로 구할 수 있고, epsilon이 작아짐에 따라서 이러한 delta를 계속 구할 수 있으면 극한값이 존재하는 것이고, 만일 이러한 delta를 구할 수 없다면 극한값이 존재하지 않는다.

 

더 나은 이해를 위해 극한값이 존재하지 않는 경우의 예시를 들어보자.

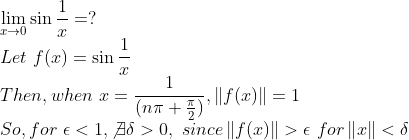
epsilon이 1/2로 주어졌다고 할 때, x가 작아질 때, x가 특정 조건에 걸리면 자꾸 거리가 1로 되어 epsilon보다 큰 경우가 생기므로 이 경우에는 위의 조건을 만족하는 delta가 존재하지 않는다.

 

만일 a가 무한대로 간다면

만일 b가 무한대로 간다면

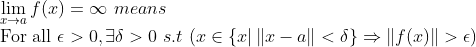
음의 무한대도 이런 방식으로 정의할 수 있다.

---

사실, 함수의 연속성도 이러한 정의에서 크게 벗어나지 않는다.

 

(함수의 연속)

그리고 어떤 구간 안의 모든 x에서 f가 연속이면 f는 그 구간 안에서 연속이라고 한다.

 

보면 알겠지만, 극한의 정의에서 b가 단지 f(a)로 바뀌었을 뿐이다.

그러므로 우리가 전에 알고 있던 연속의 정의와 비교하면 똑같다는 것을 알 수 있다. (다만, x=a 근방에서 f(x)가 정의되는 모양새가 약간 다르긴 하다. 이에 대한 논의는 해석학 참고)

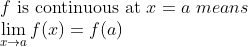
다음 챕터에서는 함수의 미분에 대해서 보도록 하자.