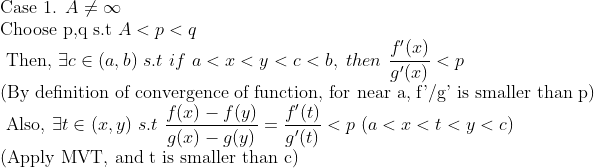이번 챕터에서는 테일러 정리에서 필요한 코시 평균값 정리를 소개하고, 이와 관련된 로피탈의 정리를 소개한다.
사실 여기서도 결국에 평균값 정리의 엄밀한 증명은 해석학으로 넘기고, 고등학교 때 배웠던 평균값 정리를 이용하여 코시 평균값 정리와 로피탈 정리를 끌어낼 것이다.
먼저 고등학교 때 배운 평균값 정리에 대해 복습해보자.
*****(Mean Value Theorem(MVT))

(NOTE) 대부분 연속조건(나중에는 적분조건)의 경우 닫힌 구간, 미분가능조건의 경우 열린 구간을 사용한다.
간단하게 설명하자면 평균변화율의 값을 가지는 순간변화율의 point가 (a,b) 안에 존재한다는 것이다.
여기서 잠깐 해석학에서 볼 평균값 정리 증명의 Tip을 보자면, 중요하게 보아야 하는건 f(x)의 미분가능성보다도 저 열린 구간, 닫힌 구간(????)에 더 중요한 point가 있다.
어쨌거나 이 MVT는 이어질 증명에서 계속해서 사용되므로 아주 중요한 정리이다. (심지어 MVT라고 약어로도 많이 쓴다.)
코시 평균값 정리는 이 MVT를 두 개의 함수에 대해서 조금 더 일반화한 정리이다.
(Cauchy's Mean Value Theorem)
f(x), g(x)는 MVT에서 요구하는 조건을 만족한다고 하자. (연속, 미분가능)
그러면

(증명)
다음과 같은 함수를 생각해보자.

결론적으로는 그냥 두 개의 함수를 잘 합쳐서 평균값 정리를 사용한 것 밖에는 없다.
로피탈의 정리는 코시 평균값 정리를 조금 더 이용해서 극한값을 편하게 구하기 위해 사용된다. 다만 항상 조건들을 조심하면서 사용해야 한다.
(L'Hospital's rule)

여기서 고등학교 때 어떻게 풀었는지 생각해보자.
뭔가 그냥 극한값 구하기는 어려워 보이고, 분자와 분모가 미분하기 좋아보일 때, 그냥 분자와 분모를 미분해서 그 극한값을 구해서 넣지 않았었는가???
그러나 정확하게는
1. 분자, 분모를 미분한 것이 수렴해야 함
2. 분자, 분모가 0/0, inf/inf인 상황에서만 사용해야 함
즉, 0/0이나 inf/inf 인 상황에서 미분했을 때 수렴하면 사용해야 하고, 그 이외의 상황에서는 사용하면 안 된다.
(사실, inf/0 이면 그대로 inf이고, 0/inf 이면 0일 것이 자명함)
사실 더 정확한 정리는 다음과 같다.
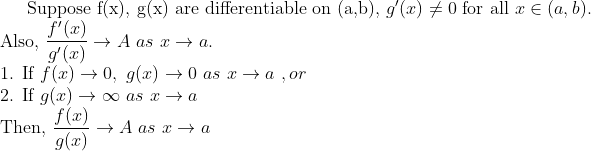
(2번의 f(x) 조건만 없어짐)
(증명)
일단 정확한 증명을 적어놓긴 했지만, 이 증명을 실제로 이용한다기보다는 고등학교때 쓴 것처럼 극한값을 로피탈을 이용해 푸는게 간편한 경우 사용한다.
왜냐하면 상당히 보편적으로 사용할만한 증명법이라기보다는 꽤 tricky하기 때문에....
그래서 왠만하면 로피탈을 고등학교 과정에서는 쓰지 말라고 하는 것이기도 하다. 정확한 증명을 싣기엔 너무 어렵고, 그렇다고 야매로 하다간 조건에 대한 이해가 부족해지고, 오히려 로피탈을 안 쓰고 접근하는 방법이 사실 chain rule(합성함수 미분) 같은 notion을 이해하는데 기초가 되기 때문에...
그리고, 이러한 사실들은 문제 내는 사람들도 모두 알고 있는거라 로피탈을 못 쓰도록 일부러 미분하면 식이 더러워지거나 수렴하지 않도록 내는 경우가 허다하다.
이번 챕터에서는 주제와 조금 벗어난 내용(로피탈)을 다뤘지만, 로피탈을 제외하고 MVT나 함수의 극한 정의는 중요하므로 다시 한번 체크하고 넘어가는 것도 좋다.
다음 챕터에서는 다시 테일러 급수 문제로 돌아가 테일러 정리를 증명해보자
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 5-2. 결국엔 테일러 급수만 이용하게 됨... (Taylor Series) (0) | 2023.01.05 |
|---|---|
| (미적분학) 5-1. 테일러 정리까지 오느라 수고하셨습니다...(Little-O Notation, Taylor Theorem) (0) | 2023.01.05 |
| (미적분학) 3-3. 필요한건 미분이라구!!! (Differentiation of function) (0) | 2023.01.05 |
| (미적분학) 3-2. 근데 우리가 필요한건 수열보단 함수 아니었나?? (Convergence, Continuity of function) (0) | 2023.01.05 |
| (미적분학) 3-1. 테일러 정리를 들어가기 전에...(Power Series, Convergence Radius) (0) | 2023.01.05 |