저저번 챕터에서 테일러 정리에 대해서 잠시 소개한 적이 있었지만, 다시 한번 간략히 복기해보면
테일러 정리는 미분가능한 함수를 다항함수(Polynomial) 꼴로 근사하는데 쓰이는 정리이다. 다만, 이 근사한다(approximate)는 표현을 다루기 위해서 잠시 Little-O notation에 관한 내용을 다루고 넘어간다.
(Big-O Notation)
아마 컴공이나 알고리즘 관련하여 공부하였으면 많이 봤을 개념이다.
쉽게 말해 Big-O Notation은 "주어진 함수 f(n)가 다른 어떤 잘 아는 함수 g(x)의 scale로 움직인다 (이를 f(n)=O(g(n))로 표현한다.)" 라는 개념이다.
즉, Big-O Notation의 목적은 정확한 값의 측정보다는 대충 이 정도로 움직인다라는 것을 보여주는 것이다.
g(x)에 들어가는 대표적인 함수들은 n, n^2, .... , n!, log n, nlog n,..... 같은 간단한 함수들이 있다.
예를 들어 f(n)=O(n!) 이면 f(n)이 엄청나게 빠르게 증가한다는 것이고, f(n)=O(log n)이면 f(n)아주 천천히 증가한다는 뜻이다.
말로 하면 오히려 조금 어려울 수도 있으므로 예시를 하나 든다.
예를 들어 n개의 박스 중 하나에 오리 한마리를 넣어놨다고 하자. 그리고 박스 하나를 들춰보는데에 1초의 시간이 걸린다고 하자.
그러면 오리를 찾는데 걸리는 평균 시간을 생각하면 당연히 (n/2)초 일 것이다. (물론 첫번째 박스에서 찾을 수도 있지만 평균이니까!)
이 때, 상수배(1/2)는 그냥 쿨하게 무시한다.(정확한 값을 요구하는 것이 big-O notation의 목적은 아니므로) 그러므로 오리를 찾는데 걸리는 평균 시간의 함수를 f(n)이라고 하면 f(n)=O(n) 이 된다.
정확한 정의는 다음과 같다.
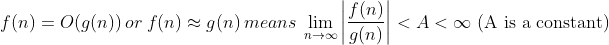
즉, "n이 증가할수록 f(n)이 기껏해야 g(n)의 상수배 만큼 움직인다" 라는 개념으로 해석하면 된다.
상수배를 무시하는 것도, 어차피 저 limit이 constant인지 아니면 무한대로 발산하는지가 중요한거지 limit 값 자체가 중요한게 아니기 때문에 가능하다.
(Little-O Notation)
Big-O Notation과 비슷한 개념으로 Little-O Notation이란 개념도 존재한다.
정의는 다음과 같다.
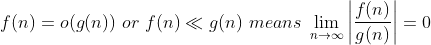
즉, "n이 증가할수록 f(n)이 g(n)보다 아주 느리게 증가한다" 라는 개념으로 해석하면 된다. 이 경우에도 상수배는 저 limit이 0이 되는데에 아무런 영향을 주지 못하므로 그냥 무시한다.
예를 들면 f(n)=n^3+sin(n) 이라면 f(n)=O(n^3), f(n)=o(n^4) 등으로 표현 가능하다.
(Note) (Big-O, Little-O notation의 g(n)은 하나가 아닐 수도 있다.)
이 Notation을 테일러 정리에 적용하여 요약하면 다음과 같다.
n번 미분가능한 함수 f(x)를 다항함수(Polynomial) 꼴로 근사하는데 근사할 때 생긴 오차항이 bounded되어있다.
(Taylor Theorem)
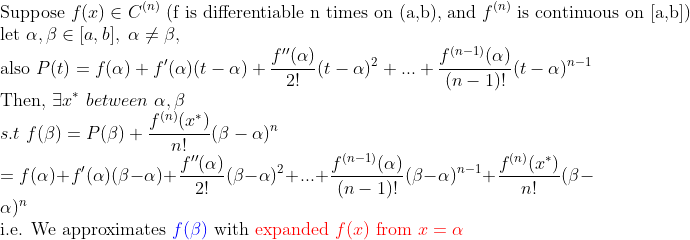
(증명)
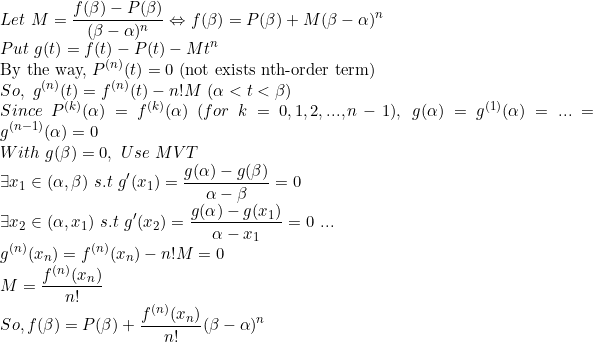
여기서 M은 alpha와 beta가 주어져 있으므로 하나의 상수일 뿐이고, 또한, MVT를 순차적으로 이용해 M의 값을 유도해내었다. 단, 여기서는 alpha나 beta, x_1,... 등의 정확한 대소관계가 중요하진 않으므로 그냥 그렇게 되는구나 하고 대충 넘어가긴 했다.
즉, 정리하자면 n번 미분가능하고 그 결과가 연속함수인 f(x)를 x=alpha을 기준으로 근사한 다항함수는
위에 있는 다항함수 P(beta) 이고, 나머지 오차항은 x-star가 포함된 항으로 표현된다.
0을 기준으로 전개한 것이 아니라서 약간의 혼란이 있을 수도 있지만
위는 alpha를 기준으로 함수를 전개하였고, 이를 이용해 f(beta)의 값을 근사하는 과정이라고 생각하면 된다.
beta는 저 구간 안의 임의로 잡아준 것이므로 그냥 beta를 x라고 생각할 수 있다.
그리고 가장 중요한 것은 여기서 오차가 다음과 같이 주어지는데
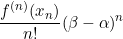
x_n은 alpha와 beta 사이에서 존재하고, n번 미분한 함수 f^(n)은 alpha와 beta에서 정의되어 있으므로 f^(n)(x_n)은 주어진 값이라고 생각할 수 있다(not infinity). 그러므로 결국 오차를 그냥 구한거나 마찬가지이다!
즉, 오차 M은 다음과 같이 bounded 되어있다.
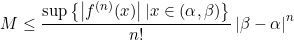
단지 위에서 x_n이 alpha와 beta사이에서 존재하니까 supremum(maximum)값으로 조금 일반화하였을 뿐이다. (supremum에 관한 내용은 해석학 참고, 간단히 얘기하면 여기서의 supremum은 maximum이라고 생각할 수 있다.)
또한, 저 sup값은 bounded이다. (supremum이라고 생각하면 당연히 존재하는거고, maximum이라고 생각하면 n번 미분한 함수 f^(n)은 연속이라서 최대/최소 정리를 생각하면 언제나 저 maximum값은 존재한다고 대충 넘어가자. 물론, 열린 구간이라 정확한 설명은 아니지만, 여기서 supremum에 관한 논의를 안할거라서...)
그러므로 결론은 저 M=O(?/n!)이라는 것이다! (factorial이라 엄청나게 빠르게 줄어든다)
((Note) 지수함수보다 factorial이 훨씬 더 강력하게 작용한다.)
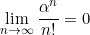
?부분에는 n번 미분한 함수에 따라 조금씩 바뀌겠지만 n! 자체가 엄청나게 강력하기 때문에 테일러 정리는 꽤나 강력한 도구가 된다. (다음챕터에서 저 ?에 따라 오차가 안 줄어드는 상황을 발견할 것이다.)
일단 여기까지는 테일러 정리의 이론적인 내용이고, 다음 챕터에서는 이를 이용한 테일러 급수에 대해서 조금 더 살펴볼 것이다.



