이전 챕터까지 테일러 정리에 대해서 정리하였는데, 지금까진 많이 이론적인 내용들이 강해서 꽤나 어려웠을거라고 생각한다.
그러나 이번 챕터에서는 고리타분한 이론에서 조금 벗어나서 함수에 직접 테일러 정리를 적용해본다.
(Taylor Series)
테일러 정리에서 n이 무한대로 가면, (즉, f(x)가 무한번 미분가능할 때(따라서 언제나 미분 결과는 연속))
다항함수 P(x) -> Power Series P(x)로 생각할 수 있고, 이 때의 power series P(x)를 테일러 급수(Taylor Series) 혹은 테일러 전개(Taylor Expansion)이라고 한다.
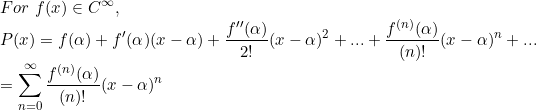
(이 경우에는 x=alpha를 기준으로 전개)
먼저, 이 P(x)의 의미가 있는 구간은 오직 수렴반경 안(혹은 x=수렴반경)이다.
그러나, 이 수렴반경 안에서도 P(x)가 항상 f(x)와 일치한다는 보장은 없다. 일단, 테일러 정리에서 본 오차항은 O(?/n!)이라고는 했는데 supremum을 구할 때, 예상외로 그 값(?)이 n!보다 커질 수도 있기 때문이다....
그렇다면 이 P(x)와 f(x)는 언제 일치하는걸까???
그건 이 전 챕터에서도 언급한, 이름부터 오차항인 바로 그 오차가 0에 수렴해야한다. 그런데 저 테일러 급수의 일반항은 우리가 보았던 바로 그 오차항(x^n은 제외한)이다.
즉, (P(x)로 f(x)를 근사할 수 있다)와 (오차가 0으로 수렴)은 동치라는 것이다.
(Analytic function in Taylor Series)
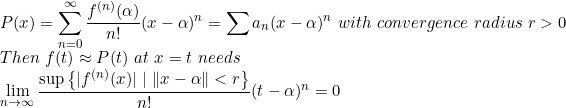
만일, 오차가 0으로 수렴하면 이 함수 f(x)는 analytic(해석적)하다고 하고, 아니면 non-analytic(비해석적)이라고 한다.
즉, analytic function은 taylor series로 근사할 수 있다.
Ex1) Exponential function
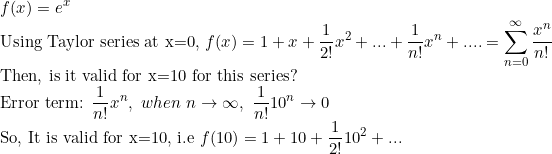
((Note) 이 경우 수렴반경은 무한대)
Ex2) Non-analytic function
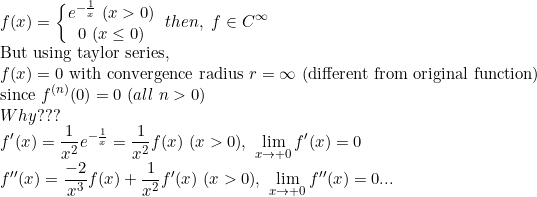
((Note) 이 경우 power series가 결국 P(x)=0이므로 수렴반경 역시 무한대)
즉, 원래 함수와 테일러 급수가 일치하지 않는다.
자주 이용하는 테일러 급수
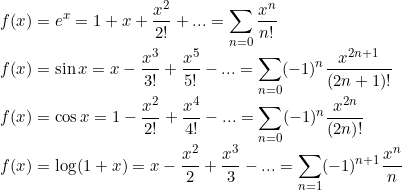
여기 제시된 모든 함수는 각 급수의 수렴반경 안에서 테일러 급수가 원래 함수와 일치한다.
(log의 경우만 수렴반경이 1, x=1일 때에도 원래 함수와 일치한다.(error term check))
(나머지는 수렴반경이 모두 무한대)
여기까지 미분 가능한 함수의 가장 강력한 근사 방법인 테일러 정리, 테일러 급수에 대해서 알아보았다.
다음챕터에서는 한때 수능에서 어렵다고 소문났던 행렬(Matrix)과 그에 관련된 중요한 개념인 선형사상(Linear Mapping)에 대해서 알아보도록 하자.



