(선형대수학 참고링크)
(선형대수학) 6. 선형사상과 행렬 (Advanced!): https://0418cshyun.tistory.com/156
(선형대수학) 6. 선형사상과 행렬 (Advanced!)
이제부터는 Ax=0, Ax=b를 푸는 것을 넘어서 => 여러 가지 Vector Space를 보았으니, 이 Space들 사이의 기하학적 관계를 보려고 한다. (참고링크) (미적분학) 6-2. 이상하게 계속 보이는 선형사상 개념(Linear
0418cshyun.tistory.com
일단 사상(Mapping)이란 무엇인지 알아보자.
(Mapping)
간단히 말해 어떤 값을 다른 값에 대응시키는 것을 말한다. (값이 굳이 수일 필요는 없다(ex. 함수를 대응시킬수도...))
함수(function)하고 비슷한 개념이지만 함수는 같은 input에 다른 output이 나올 수 없지만 Mapping은 이런 것에 대해 자유롭다.
예를 들어서 real-plane에서 x=1은 함수가 아니지만, Mapping(T)을 이용하면 다음과 같이 표현할 수 있다.
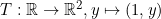
즉, 1차원 실수축을 x=1로 mapping 할 수 있다.
앞 챕터에서도 언급했지만 다변수 함수를 다루기 위해서 행렬을 사용한다고 했는데, 어떻게 보면 m by n 행렬(A)도 성분이 m개인 벡터(x)를 곱하면 성분이 n개인 벡터(y)를 뱉기 때문에 행렬 A(정확히는 left-product)도 mapping의 일종이라고 할 수 있다.
즉,
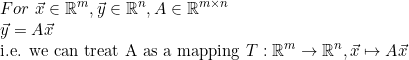
그렇다면 선형(Linearity)은 무엇일까?
(선형사상(Linear Mapping))
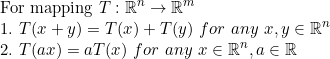
1과 2를 모두 만족하는 사상 T에 대해서 T는 선형사상(Linear Mapping)이라고 한다.
1,2를 합쳐서 쓸 수도 있는데, 다음과 같다.
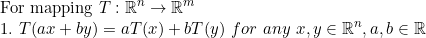
앞에서 행렬도 mapping의 일종이라고 했는데, 그러면 선형사상과 행렬은 어떤 관계가 있을까?
★★(Matrix and Linear Mapping)
모든 선형사상과 행렬로 표현 가능하다. 또한, 모든 행렬은 선형사상으로 표현 가능하다.
즉, 선형사상과 행렬은 같은 표현이다.
(증명)
1. 행렬은 선형사상이다.
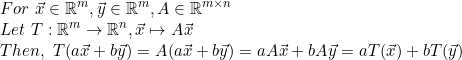
그러므로 행렬 A는 선형사상 T로 표현가능하다.
2. 선형사상은 행렬이다.
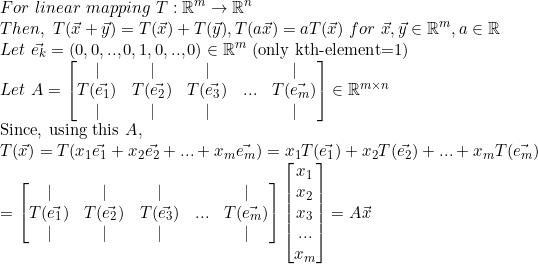
그러므로 선형사상 T는 행렬 A로 표현 가능하다.
이 증명에서 이렇게 단위벡터로 쪼개는 표현과 행렬을 행벡터로 쪼개는 표현은 많이 쓰이므로 다시 한번 체크해보자!
이번 챕터를 정리하면
일단, 다변수를 다루기 위해서 다음과 같은 사상을 생각할 수 있다.
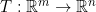
만약, 이 사상이 선형성(Linearity)를 만족한다면, 이 선형사상은 (m by n) 행렬과 동일하다.
그러므로 이제 선형사상을 다룰 때에는 보다 익숙한 "행렬"을 사용하면 된다.
-> 선형대수(Linear Algebra)가 행렬을 다루는 이유이다.
이번 챕터를 마무리하면서 다음과 같은 질문을 남길 수도 있다. "그렇다면 선형성을 만족하지 않는 사상은???"
여기에 간략히 답을 하자면 너무 어렵다는 것이다. 일단, 선형성을 만족하지 않는다는 것은 너무 범위가 넓고, 다루는 방법도 케이스마다 다르고 너무 어렵다. 그러므로 비선형성을 가진 사상, 혹은 시스템이 있다면 대부분 최대한 선형화(Linearization)를 시켜 선형사상(시스템)으로 바꿔서 다루게 된다.
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 7-2. 역행렬 계산이 왜 이렇게 복잡하지? (Determinant) (1) | 2023.01.05 |
|---|---|
| (미적분학) 7-1. 역행렬을 위한 선형대수 기본 지식 (Linear Combination / Independence) (0) | 2023.01.05 |
| (미적분학) 6-1. 한때는 어려웠던 행렬...과 선형대수의 시작(Matrix, Linear Algebra) (0) | 2023.01.05 |
| (미적분학) 5-2. 결국엔 테일러 급수만 이용하게 됨... (Taylor Series) (0) | 2023.01.05 |
| (미적분학) 5-1. 테일러 정리까지 오느라 수고하셨습니다...(Little-O Notation, Taylor Theorem) (0) | 2023.01.05 |



