(Note) 이번 챕터는 행렬의 기본적인 성질을 알고 있다는 가정 하에 작성하였습니다.
저번 챕터에서는 선형사상과 행렬 사이의 관계에 대해서 알아보았는데, 이번에는 조금 더 선형대수학 쪽으로 방향을 틀어서 역행렬(Inverse Matrix)의 존재조건에 대해서 알아보도록 한다.
다들 알고 있겠지만, 행렬의 큰 특징 중에는
1. 곱셈의 교환법칙이 성립하지 않는다.
★2. 곱셈의 역원(역행렬)이 존재하지 않을 수도 있다.
이 중 1번은 나중에 추상대수학에서 아벨군을 다루면서 다루도록 하고, 우리는 2번 특징에 대해서 조금 더 살펴 볼 것이다.
일단, 역행렬이 필요한 이유는 연립방정식을 보면 알 수 있다.

저기서 우리가 원하는 x,y를 구하기 위해서는 2 by 2 행렬을 지워야 하는데, 이를 곱셈의 역원(역행렬)로 지운다. 그래서 역행렬이 필요한데, 역행렬이 존재하지 않을 수도 있다는 것은 이런 방법이 불가능할 수도 있다는 것이다. 즉, x,y를 구할 수 없다는 것이다. (더 정확하게는 유일한(unique) (x,y)를 구할 수 없다.)
"왜 x,y를 구할 수 없는 것일까???"
이 질문에 답을 하기 위해 좌표평면에서 저 2개의 방정식을 생각해보자.
각 방정식은 좌표평면에서 직선의 방정식이고, 그렇다면 (x,y)는 두 직선의 교점이다. 그러면 유일한(unique) (x,y)를 구할 수 없다는 말은 교점이 없거나 교점이 여러 개라는 이야기가 된다.
그렇다면 언제 교점이 없거나 교점이 여러 개가 될까?
1. 두 직선이 평행하면 교점이 없다. (a/c=b/d, e/f is not equal to a/c)
2. 두 직선이 일치(동일)하면 교점이 여러 개가 된다. ( a/c=b/d=e/f)
사실 이 두 케이스를 행렬의 입장에서만 생각해보면 다음과 같다.
2 by 2 행렬이 하나의 직선(1차원)에 관한 정보만 가지고 있다. (정보의 부족)
왜냐하면 1, 2를 구분하는 건 위의 식에서 e, f이고, a,b,c,d는 이를 구분해줄 수는 없기 때문이다.
결론적으로 (x,y)를 구하기 위해서는 변수가 2개라 2차원의 정보가 필요한데, 행렬이 1차원 정보만 가지고 있으니 (x,y)를 구할 수가 없다라는 것이다.
자, 그러면 저 행렬이 2차원에 관한 정보를 가지고 있는지 어떻게 확인할까?

이를 이용하면 역행렬이 없을 때는 행렬의 행벡터(혹은 열벡터)가 서로 평행하다는 것을 알 수 있는데, 이 방법을 통해 행벡터들로 2차원을 만들 수 있는지(Span)에 따라서 2차원 정보를 가지는지 확인할 수 있다.
간단히 설명하자면, 행벡터가 (1,1),(1,2)라면 좌표평면에 있는 모든 점은 이 두 벡터에 의해서 표현이 가능하지만(2차원 정보를 가지고 있음),
행벡터가 (1,1),(2,2)이라면 오직 y=x에 있는 점만 표현이 가능하고, 그 외의 점은 표현이 불가능하다. 그러므로 이 행렬은 1차원의 정보(y=x)만 가지고 있다.
이제 2차원에서 유한차원 n차원(n by n 행렬)으로 확장해보자.
이 경우에도 2차원과 똑같은 방법으로 접근한다.
행벡터는 n개가 있을 것이고, 이 n개의 행벡터로 n차원을 만들 수 있는지(span) 확인한다.
만일, 어떤 행벡터가 다른 행벡터에 의해서 만들어 질 수 있다면, 그 행벡터는 자신만의 unique한 정보를 가지지 않으므로, 한 차원의 정보를 더 얻을 수 있는 기회를 잃어버렸다고 할 수 있다. 그러므로 만일 그런 행벡터가 m개가 있다면, 이 행렬은 (n-m)차원의 정보를 가지고 있을 것이다.
이렇게 행렬이 얼만큼의 차원의 정보를 가지고 있는지를 rank라고 할 수도 있다. 즉, 위의 경우에선 rank(A)=n-m 이 된다.
자 이제, 역행렬 얘기로 다시 돌아와보자.
위의 내용을 정리하면 역행렬을 가지려면
1. n개의 행벡터로 n차원으로 span 가능해야 함.
2. rank(A)=n
3. 각 행벡터가 다른 행벡터로 표현이 되면 안된다(linearly independent).
이 3개는 모두 동치이고, 여기에선 3번 방법에 관해서 살펴본다. 1번과 2번 내용은 선형대수학 카테고리를 참고바란다.
여기서는 잠시 용어를 정리하고 간다.
(Linear Combination)

(Linearly dependent / Linearly independent)

즉, 한 벡터가 다른 벡터에 의해 표현되는 경우 linearly dependent라고 하고, 그런 벡터가 없으면 linearly independent라고 한다.
Linearly independence를 확인하려면 일일히 각 벡터를 확인하기 보단 다음과 같은 방법을 이용하면 편리하다.
(Test for Linear Independence)

모든 a가 0인 경우 Trivial Solution을 가진다고 한다.
(증명)
본 정리의 대우를 증명하면 된다.
1. 만일 Trivial solution을 가지지 않는다면(해가 (0,0,0,...0)이 아니라면)
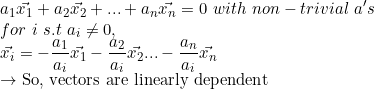
하나의 벡터 x_i에 대해서 정리를 할 수 있으므로 linearly dependent.
2. 만일 벡터들이 linear dependent하다면,
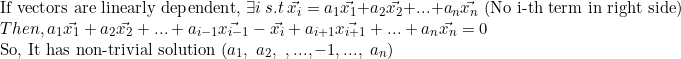
자, 여기까지 Linear Independence에 관해 살펴보았다.
앞에서 나온 내용과 합치면, 역행렬을 가지려면 행벡터들이 linearly independent해야 한다 라는 내용으로 요약할 수 있다.
다음 챕터에선, 역행렬을 가지는지 판단하기 가장 쉬운(수치적으로 계산하기 가장 쉬운) 행렬식을 다뤄보도록 하겠다.
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 8. 내적이 있으니까 외적도 있겠지... 로피탈보다 오히려 더 중요하고 써먹을 수 있는 외적 (Outer Product) (0) | 2023.01.05 |
|---|---|
| (미적분학) 7-2. 역행렬 계산이 왜 이렇게 복잡하지? (Determinant) (1) | 2023.01.05 |
| (미적분학) 6-2. 이상하게 계속 보이는 선형사상 개념(Linear Mapping, Matrix) (0) | 2023.01.05 |
| (미적분학) 6-1. 한때는 어려웠던 행렬...과 선형대수의 시작(Matrix, Linear Algebra) (0) | 2023.01.05 |
| (미적분학) 5-2. 결국엔 테일러 급수만 이용하게 됨... (Taylor Series) (0) | 2023.01.05 |



