저번 챕터에서는 linear combination에 관해 알아보았다면, 이번에는 역행렬 계산과 관련이 있는 행렬식(Determinant)에 대해 알아보도록 한다.
행렬식 자체가 정사각행렬(n by n matrix)에서만 정의가 되므로 여기선 다른 언급이 없으면 n by n matrix라고 생각한다.
일단 행렬식의 정의부터 알아보자.
(Determinant)
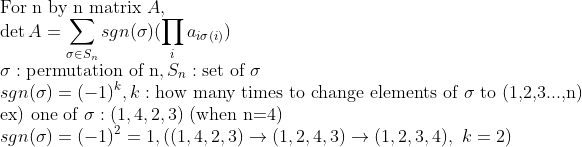
뭔가가 많이 복잡해보이지만, 일단 순서대로 설명하면 그렇게 어려운 내용은 아니다.
일단 저 sigma는 (1,2,3,...,n)의 permutation(중복되지 않게 줄 세우기)로 위에서 본 예시를 보면 이해가 될 것이다.
또한, 여기서 k를 다음과 같이 생각한다.
k=(주어진 sigma를 원소끼리 서로 자리 바꿔치기를 해서 (1,2,3,...,n)을 만들 때 서로 자리를 바꾸는 횟수)
위의 예에서는 k=2가 될 것이다.
이 때, sgn함수는 (-1)^k 로 정의한다.
이렇게 해서 모든 permutation(sigma)에 대해 sgn과 각 row들의 permutation을 모두 곱한 것(위 식에서 큰 파이가 모두 곱한다는 뜻이다.)을 모두 더하면 우리가 원하는 det A가 된다. 아직도 이해가 안되면 아래의 3 by 3 matrix 예시를 보자.
(NOTE) k를 계산할 때, 굳이 최소 횟수를 구하지 않아도 된다. 즉, (1,2,3...,n)으로 바꾸는 횟수는 홀/짝(parity)이 보존된다.
(Example)
이미 알고 있는 2 by 2 matrix는 생략하고 (det (A) = ad-bc)
3 by 3 matrix A에 대해서 생각해보자.
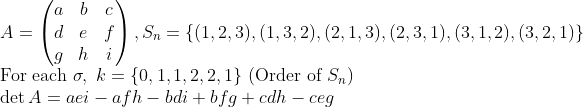
이를 다음과 같이 설명할 수도 있다.

A에서 열 하나를 잡고, 그 열의 각 원소를 택해서 그 원소의 행과 열을 제거한 행렬의 행렬식을 계산하는 방식으로 행렬식을 계산할 수도 있다.
사실 왜 이런식으로 행렬식이 계산이 되는가는 역행렬을 직접 계산하는 과정에서 알 수 있는데, 이는 선형대수 카테고리를 참고바란다.
딱 보면 알겠지만, n=2,3 인 경우는 이를 이용해 쉽게 계산이 가능하지만, n=4 이상인 경우에는 손으로 계산하기 난감해진다. 그래서 이를 좀 편하게 계산하기 위해서 다음과 같은 성질들을 이용한다.
(성질 1)
행렬식은 각 열에 대해서 선형사상이다.
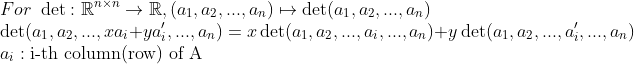
(증명)
1. 상수배 증명(Linear mapping 2번 in 7-1)

determination 정의를 생각해보면 permutation을 구해서 각 행렬 성분을 선택할 때, i번째 열을 선택할 때, 원래 값보다 x배한 값이 들어가는 것이므로 각 permutation(sigma)마다 x배한 값이 들어간다. 그러므로 상수배 조건을 만족한다.
2. 합 증명(Linear mapping 1번 in 7-1)

이번에도 detereminant 정의를 생각해보면, 각 permutation을 구할 때, i번째 열을 선택할 때, 그걸 2개(a_i, a_i')로 쪼개면 된다. 즉, 각 sigma의 항마다 2개씩 쪼개진다. 그러므로 위의 식을 만족한다.
(Corollary 1)
이를 이용하면 행렬의 상수배 kA에 대해서
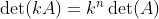
임은 자명하다. (모든 행이 k배이므로)
여기서 헷갈리지 말아야 할 것은, determinant는 각 행에 대해서 선형사상이지, 행렬에 대해서 선형사상이 아니다.
(성질 2)
행렬에서 열만, 혹은 행만 서로 (1번만) 바꿔치기하면 행렬식의 크기는 같고 부호만 달라진다.
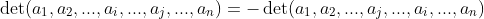
(증명)
간단하게, 사실 determination의 정의에서 행이나 열을 1번 서로 바꿔치기 하면 각 permutation의 k가 원래값보다 1씩 늘어난다고 생각하면 되므로, sum할 때, sgn함수에 의해서 각 항의 부호가 바뀐다. 그러므로 행렬식의 부호가 달라진다.
(Corollary 2)
행렬에서 열만, 혹은 행만 서로 (n번만) 바꿔치기하면 행렬식의 크기는 같고 (-1)^n 만 곱하면 된다.
(성질 3)
행렬에서 서로 같은 행/열이 존재하면 det A=0이다.

(증명)
(성질 2)에서 바로 유도 가능하다.
위의 두 a_i를 바꾼다고 하면,
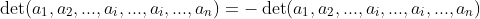
을 만족해야 한다. 그러므로

(성질 4)
어떤 행/열이 linearly dependent하면 det A=0이다.
즉, det A가 0이 아니면 linearly independent이다.
(증명)
(성질 3)을 이용하면 바로 증명가능하다.
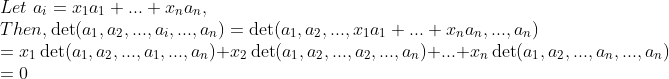
(성질 5)
만일 어떤 함수가 (성질 1), (성질 2)를 만족한다면 이 함수는 determinant 함수이다.
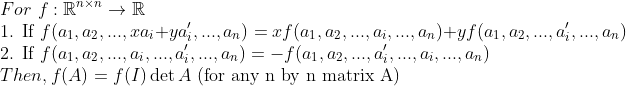
(증명)

각 행렬 성분을 단위벡터로 다 쪼개서 정리하는 것으로 위 정리의 증명을 할 수 있다. 이 때, 전치행렬(Transpose)과 원래 행렬의 행렬식은 동일하다.(Permutation 잡아 성분 택할 때, 결국 같은 것을 택하게 된다.)
(성질 6)
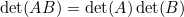
(증명)
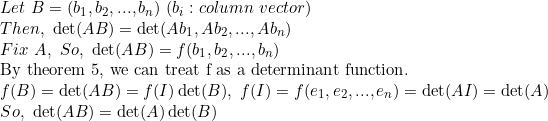
(성질 5)를 이용하면 바로 구할 수 있다.
(Corollary 6)
만일 A의 역행렬이 존재한다면 다음과 같은 식이 성립한다.

(증명)
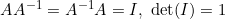
위의 식에 det만 태워서 식 정리하면 바로 구할 수 있다.
(성질 4)와 (Corollary 6)을 종합해보자.
역행렬이 존재하려면 linearly independent 해야 하므로
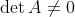
을 만족해야 한다는 것이다.
det(A)=0 인 경우 (당연히) 역행렬이 존재하지 않는다. 라는 사실을 알 수 있다.
즉, 앞 챕터에서 나온 역행렬 존재조건을 확장하면
| 1. n개의 행벡터가 n차원으로 span 가능 2. rank(A)=n 3. n개의 행벡터가 linearly independent 4. det(A)가 0이 아니다. |
이 4개의 조건이 모두 동치가 된다.
역행렬을 직접 구하는 방법은 선형대수 카테고리를 참고하고, 다음 챕터에서는 잠시 벡터 문제로 가서 2차원, 3차원 문제에 활용되는, 특히 행렬식과 연관된 개념인 외적(outer product)에 대해서 살펴보도록 한다.
'Mathematics > 미적분학' 카테고리의 다른 글
| (미적분학) 9-1. 알면 아주 편한 복소평면 개념(Complex plane, polar coordinate) (0) | 2023.01.05 |
|---|---|
| (미적분학) 8. 내적이 있으니까 외적도 있겠지... 로피탈보다 오히려 더 중요하고 써먹을 수 있는 외적 (Outer Product) (0) | 2023.01.05 |
| (미적분학) 7-1. 역행렬을 위한 선형대수 기본 지식 (Linear Combination / Independence) (0) | 2023.01.05 |
| (미적분학) 6-2. 이상하게 계속 보이는 선형사상 개념(Linear Mapping, Matrix) (0) | 2023.01.05 |
| (미적분학) 6-1. 한때는 어려웠던 행렬...과 선형대수의 시작(Matrix, Linear Algebra) (0) | 2023.01.05 |



