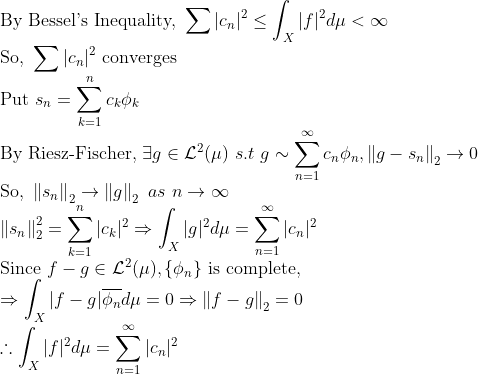(참고)
(해석학) 13-1. 공대의 친구, 푸리에 급수(Meaning of Fourier Series): https://0418cshyun.tistory.com/78
(해석학) 13-1. 공대의 친구, 푸리에 급수(Meaning of Fourier Series)
(NOTE) 여기서는 공대에서 쓰이는 개념(예를 들어서, Frequency Domain으로 변환하는 것이라던지...) 그런 거 말고, 수학적으로 어떻게 접근하는지 알아본다! 이번챕터에서는 Fouier Series(푸리에 급수)에
0418cshyun.tistory.com
(해석학) 13-2. 푸리에 급수가 그렇게 좋은가? (Convergence of Fourier Series): https://0418cshyun.tistory.com/79
(해석학) 13-2. 푸리에 급수가 그렇게 좋은가? (Convergence of Fourier Series)
이번 시간에는 푸리에 급수가 원래함수 f에 수렴한다는 것을 살펴보도록 한다. 저번 시간에 이어서 여러 근사법 중에 푸리에 급수가 가장 best한 근사법이라는 것을 확인해보자! (Bessel's Inequality)
0418cshyun.tistory.com
이번 시간에는 계속 이어서 L2-space의 Completedness를 증명하기 위해 이어간다.
Completedness를 증명하기 위해서, L2-space에서 코시수열을 정의하면
(Cauchy Sequence in L2-space)

우리가 알고 있는 코시수열 그대로이다!
(Completedness of L2-Space)
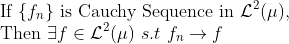
즉, L2-Space는 Complete Space이다!
(증명)

여기서 g를 아무렇게나 잡아도 되므로, 다음 성질을 만족하게 g를 잡아버리자.

(만약에 저 함수가 infinity인 구간이 꽤나 길다면, g를 그 구간에서 0으로 잡아버리면 된다!)

이 f가 우리가 원하는 f임을 보이자!
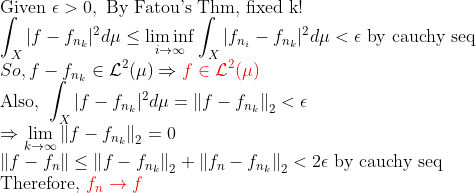
여기까지, L2-space가 Complete Space라는 것을 보였다.
더 나아가, 리만적분에서 했었던 푸리에 급수에 대해서 르벡적분으로 확장해보자.
(Orthogonal, Orthonormal Basis)

사실, 의미도 별반 다를 것이 없는게, 저 적분을 (리만적분)으로 생각하는가, 혹은 (르벡적분)으로 생각하는가의 차이 밖에 없다...
그러므로 정의도 똑같다.
또한, 이 때, 푸리에 급수를 정의한다면...
(Fourier Series in Lebesgue Sense)

여기서 잠깐!
여기선 정의만 하고, 이 푸리에 급수가 수렴하는지 아직은 모른다!
그런데, 우리가 푸리에 급수 파트에서 Bessel's Inequality를 보았다. (See 13-2)
증명과정에서 리만적분을 그냥 르벡적분으로 생각한다면... -> 그대로 성립한다! (더 필요한 거 없다!)
그러므로
(Bessel's Inequality in Lebesgue Sense)
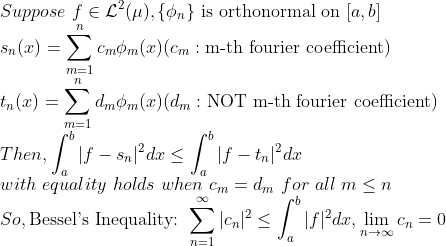
-> 즉 우리가 위에서 저렇게 sum으로 근사시킨 것이 수렴한다는 것을 알 수 있다!
(바뀐 건 리만적분가능하다는 것에서, 그냥 L2-space로 넘어온 것 밖에는 없다!)
또한, 리만적분에서 e^{inx}의 basis를 이용해서 Parseval Theorem을 보았었는데, 이번엔 르벡적분을 이용해서 증명해보자.
(Parseval Theorem in Lebesgue Sense)

여기서, 일반적인 Orthonormal basis를 쓴 것이 아니라, 특정한 basis를 썼다는 것(푸리에급수)에 유의하자!
결과는 당연히 리만적분과 동일하다!
(증명)
리만적분때와 동일하게 가자! (다만, 여기서 L2-space와 Continuous Function이 Dense하다는 관계를 이용하면 된다!)
1.
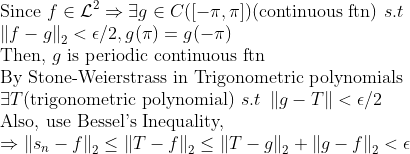
2. 앞 시간에서 L2-space에서 내적(Inner Product)에 관해서 정의했으므로, 13-2에서 했던 그대로 그냥 하면 증명 끝!
3. 2번에서 g를 f로 놓으면 된다!
(Corollary)

즉, 푸리에 급수는 L2-space에서 수렴하는 것을 알 수 있다!
(Corollary)

왜냐면, 저 적분값이 c_n이기 때문이다!
그런데, 이를 이용하면 꽤나 흥미로운 사실이 나온다.
리만적분을 이용한 푸리에 급수 파트에서
-> "결과적으로" 적분가능한 함수를 무한차원의 공간(단, basis가 Orthonormal)의 벡터로 본다는 것이었다!
-> 즉, 위에서 증명한 내용은 L2-Space를 Orthonormal basis인 무한차원의 공간으로 Mapping하는 것!
(NOTE)
단, (여기서 일반적인 Orthonormal basis가 아니라 특정한 basis를 이용했다!)
-> 일반적인 Orthonormal basis일 때의 증명은 뒤에 있다!
여기에 대해서 조금 더 이야기 하기 위해서, 힐베르트 공간(Hilbert Space)과 바나흐 공간(Banach Space)에 대한 정의를 보자.
(Hilbert Space)
Complete Metric Space(완비거리공간)을 만족하고, Inner product(내적)이 정의된 Space(내적공간)를 Hilbert Space(힐베르트 공간)이라고 한다.
-> 즉, L2-space는 완비성, Inner Product도 잘 정의되었으므로, Hilbert Space이다.
(Banach Space)
Complete Metric Space(완비거리공간)을 만족하고, NORM Space(노름 공간)를 Banach Space(바나흐 공간)이라고 한다.
-> 노름은 내적을 이용해서 정의할 수 있으므로, 바나흐 공간이 힐베르트 공간보다 더 큰 범주이다!
그러면, 우리가 무한차원공간이라고 얘기하는 저 공간은 무엇일까?
Parseval Thm in L2-space에 의해서 다음과 같이 생각할 수 있다. (만일, 일반적인 orthonormal basis에서도 성립한다고 하면)

이렇게 만든 저 H가 Complete인지 잠시 살펴보자. 사실, 저 H는 다음과 같이 쓸 수도 있을 것이다.

즉, 그냥 무한차원의 유클리드 공간이라고 생각하면 된다!
(NOTE) 하이네-보렐 정리는 이 "무한차원"에서 성립하지 않는다!
-> 사실, 우리가 초반에 본 축소구간정리는 이 "무한차원"에 구속받지 않으므로(Compact 성질만 가지면 됨)
-> 유한차원 유클리드 공간에서 했던 대로, Compact Ball을 잡을 수 있다!
-> 코시 수열이 수렴한다!
즉, 저 H는 "힐베르트 공간"이다!
Completedness의 의미를 조금 더 확장해보면 다음과 같은 성질을 얻는다.
(Completedness with Orthonormal Basis)

만일, L2-space라면...

왜 그런지 잠깐 살펴보면...
-> 모든 방향의 basis로 내적을 했더니 모두 0!
-> 만일 f의 Norm이 0이 아니라면... -> f=0일 수 없다!
-> 그 말인 즉슨, 우리가 가진 basis 말고, 다른 방향으로 더 f가 성분을 가질 수 있다는 말이 된다.
(2차원 평면을 예로 들면
-> (1,0), (0,1)과 내적을 해서 모두 0...
-> 그럼 당연히 x=(0,0)인데, 만일 3차원 공간으로 x가 움직일 수 있었다면?
-> (0,0,1)은 (1,0,0), (0,1,0) 과 내적하면 0...)
-> 그러므로 우리가 가진 basis (1,0), (0,1)으로는 저 f를 표현하기엔 부족하다!(incomplete)
-> 코시 수열의 경우에도 마찬가지이다.
-> 유리수 수열의 수렴값이 무리수인 경우가 코시 수열이 유리수에선 수렴 하지 않는다는 대표적 예시인데,
-> 즉, 무리수를 표현하기엔 유리수의 basis가 불충분하다!(incomplete)
-> 즉, Complete라는 개념은
-> 가진 basis로 주어진 (어떤 것)을 표현할 수 있는가? 라는 것이다!
일반적인 경우(Orthonormal basis)에 Parseval Thm을 증명하기 위해 다음 정리를 보자.
(The Riesz-Fischer Theorem)
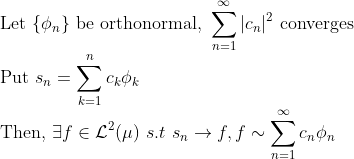
즉, 무한 차원 H의 각 원소에 해당하는 L2-space의 원소가 존재한다는 것이다.
-> 지금까지 했던거와는 반대로, 무한차원의 공간(H)을 L2-Space로 Mapping이 가능한가에 대한 답이다!
-> 또한, L2-space가 바나흐 공간이라는 것을 말해준다!!!
(증명)
이제, 일반적인 경우의 Parseval Thm을 증명해보자!
(Parseval Theorem in Hilbert Space)
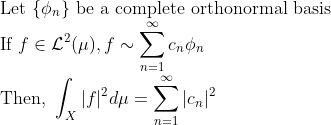
(증명)
그러므로 정리하면 Parseval's Thm 덕분에
L2-space와 Hilbert Space는 동치!
라는 것이다.
특히, 어떻게 basis를 잡던지, orthonormal이면 상관이 없다!!!

게다가 Hilbert Space이므로, 내적도 잘 정의되어 있고, Norm도 잘 정의, 그리고 Completedness까지 성립을 해준다!
-> 이러한 편의성과 성질을 기억하자!
지금까지 L2-space에 대해서만 다루었는데, 다른 Lp-space에 대해서는 어떻게 될까? -> 더 고급 강의가 필요....
여기선 간단히 L1-space에 대해서만 다루어보자!
아쉽게도, L1-space는 바나흐 공간까지만 성립하고, 힐베르트 공간의 조건은 성립하지 못한다. 즉, 내적을 정의할 수 없다!!
(문제가 발생하는 구간이, L2-space의 원소가 L1-space에 들어가지 않기 때문이다...)
그러나, Completedness 까지는 충분히 증명할 수 있다!
(Completedness in L1-space)

(증명)
먼저, 거리함수와 norm을 정의하자.

그러면 L2-space와 동일하게 증명하자.

그리고 똑같이, Fatou's Thm을 이용하면
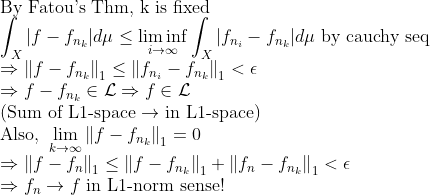
여기서, L1-space가 합에 대해서 닫혀있다고 했는데, 심플하게

임을 이용하면 된다!
일단, 여기까지 해석학에 대한 이야기를 마칩니다!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 30. 해석학 총정리 (SUMMARY) (0) | 2023.04.04 |
|---|---|
| (해석학) 29-1. 르벡적분 -> 함수공간 (Lp-Space) (0) | 2023.04.03 |
| (해석학) 28. 르벡적분과 리만적분 (Relation btw Lebesgue and Riemann) (0) | 2023.04.02 |
| (해석학) 27-3. 르벡적분과 극한 (Limit of Lebesgue Integral) (0) | 2023.04.01 |
| (해석학) 27-2. 르벡적분의 성질 (Almost all, Measure zero) (0) | 2023.04.01 |