(참고)
(해석학) 8-5. 아직 좀 부족한데....? (Improper Integral, Space of Riemann-Integrable ftns): https://0418cshyun.tistory.com/67
(해석학) 8-5. 아직 좀 부족한데....? (Improper Integral, Space of Riemann-Integrable ftns)
이번챕터에서는 저번시간에도 말했듯이 특이적분(이상적분)(Improper Integral)과 리만적분가능한 함수로 이루어진 공간에 대해서 이야기 하려고 한다. 먼저, Improper Integral에 대해서 살펴보자. (Improp
0418cshyun.tistory.com
이번 시간에는 리만적분에서 했었던 함수공간에 대한 이야기를 계속 이어나갈 것이다.
리만적분에서 함수공간을 다뤘을 때, 마지막에 리만적분가능한 함수공간은 -> Complete가 아니라고 했다!!!
그러면, 르벡적분을 이용한 함수공간은 어떻게 될까 -> 결론적으로 Complete Space(완비공간)가 된다!
먼저, 리만적분가능한 함수공간을 확장해서 르벡적분가능한 함수공간을 정의해보자!
(Lp-Space)

(NOTE)
f가 Complex-valued function으로 조금 더 일반화 된 것을 확인하자!
(NOTE)
더 나아가 p가 그냥 실수인 경우도 정의하게 된다. -> p 따라서 공간의 특성이 약간씩 달라진다!
일단, 가장 많이 사용하고, 특성이 좋은 L2-space에 대해서 생각해보자!
이 공간이 Complete임을 보이기 위해서 다음과 같은 성질들을 확인하자.
(Schwartz Inequality) -> 내적!

(증명)
리만적분때와 동일하게 증명한다!


그리고 삼각부등식도 성립한다!
(Triangular Inequality)

(증명)
(NOTE)
내적은 L1-norm인데, L2-space에서의 내적?이라고 생각할 수도 있다.
그러나, 내적의 정의 자체가 -> 내적 => "실수 or 복소수"로 나오면 되므로, 상관 없다!
(벡터의 내적이 벡터가 아니라 실수 or 복소수 라는 것을 생각하자!)
여기에 더해서 L1-space와 L2-space간의 관계를 살펴보면....

예를 들어서,
1/n은 발산하고, 1/n^2은 수렴한다는 점을 좀 이용해보면

이라는 것을 알 수 있다.
그러나, 만일 적분구간이 Finite Measure라면,

이다.
왜냐하면, 위의 내적을 이용한다면 다음과 같은 식을 얻을 수 있기 때문이다.

그러므로 "Finite Measure"를 가질 때, L2-space는 L1-space에 속해있다고 할 수 있다.

그렇다면, L2-norm은 깔끔하게 그냥 Norm으로 쓸 수 있는가를 생각해보면, 문제가 하나 있다...

이 성립하지 않기 때문이다....
그러나, "Almost All"이란 개념을 생각해본다면

이 두 함수를 같은 것(동등한 것)으로 본다면, 위의 문제도 해결이 되기 때문에
Measure Zero를 무시한다면(즉, 두 함수를 동등하게 본다면) L2-Space는 Metric Space가 된다! (metric은 L2-norm)
또한, 우리가 리만적분에서 보았던 것처럼 다음 성질을 가지고 있다.
(Dense in L2 -> Continuous Function Space)
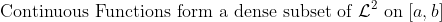
즉, 모든 L2-space의 원소에서 (l2-norm sense로) 아주 가까이에 있는 Continuous Function을 잡을 수 있다!
(증명)
1. 먼저, Characteristic Function이 L2 sense로 continuous function에 근사할 수 있는지 보자!

2. Simple Function도 그러면 L2 sense로 continuous function에 근사가능! -> 일반 Function!
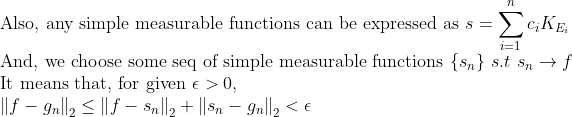
그러므로 L2-space에 있는 어떤 f도, continuous function에 근사할 수 있다!
일단 여기까지, L2-space에 관한 성질들을 보았고, 다음 시간에는 조금 더 나아가서 Complete Space라는 것을 보이자!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 30. 해석학 총정리 (SUMMARY) (0) | 2023.04.04 |
|---|---|
| (해석학) 29-2. L2-space는 Hilbert Space! (Completedness of L2-space) (0) | 2023.04.03 |
| (해석학) 28. 르벡적분과 리만적분 (Relation btw Lebesgue and Riemann) (0) | 2023.04.02 |
| (해석학) 27-3. 르벡적분과 극한 (Limit of Lebesgue Integral) (0) | 2023.04.01 |
| (해석학) 27-2. 르벡적분의 성질 (Almost all, Measure zero) (0) | 2023.04.01 |




