이번 챕터에서는 나중에 쓸 개념과 용어들을 조금 정리하고, 동등연속(Equicontinuous)에 대해서 알아보도록 하자.
지금까지 계속 나온 개념이 바로 "Uniform" 이라는 개념이다.
Uniform Continuous, Uniform Convergence를 보았는데, 유계(Boundedness)에 대해서도 "Uniform"을 이용할 수 있다.
1. Pointwise Bounded
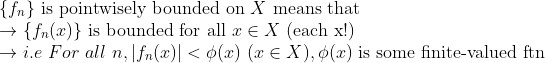
즉, 각각의 x에 대해서 모두 bounded인 것을 말한다.
2. Uniformly bounded
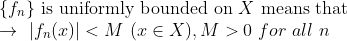
즉, 모든 x에 대해서 공통의 M으로 bounded 되어있는 것을 말한다.
굳이 설명 안해도, Uniformly Bounded이면, Pointwise Bounded인 것은 자명하다!
예를 들어서 9-1에서 본
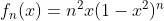
의 경우에는 Pointwise bounded이지만, Uniformly bounded는 만족하지 못한다.
1. Pointwise Bounded
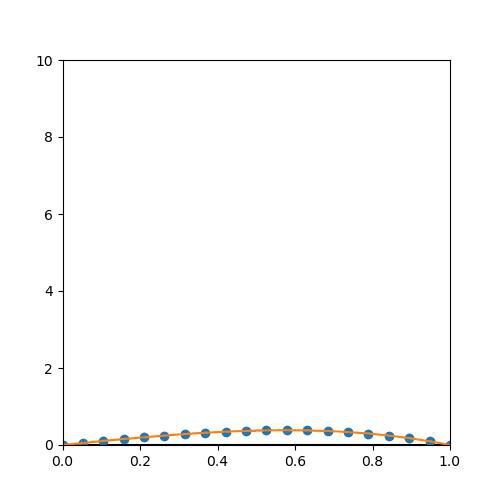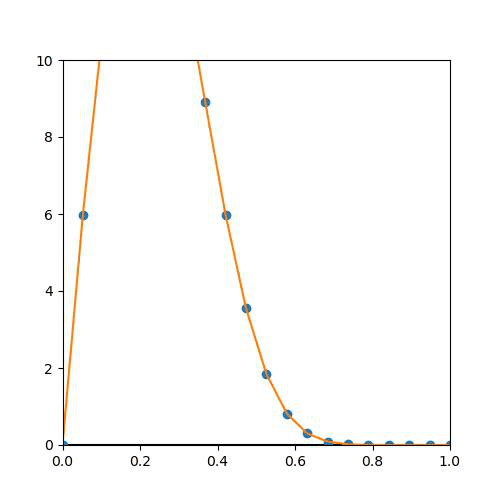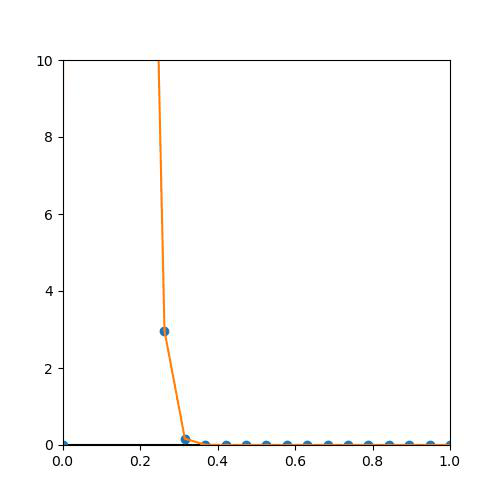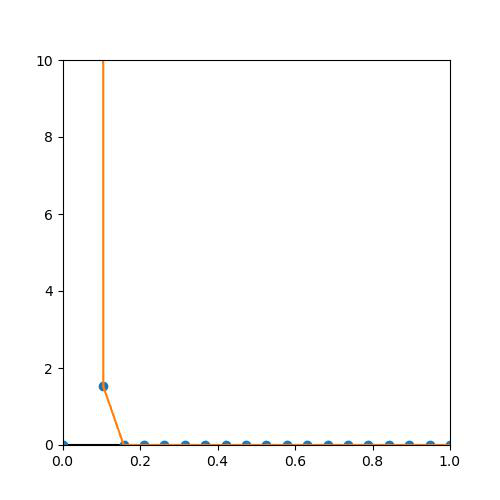
x를 Fix시켰을 때 n이 커짐에 따라 0으로 수렴하기 때문에, {f_n(x)}는 bounded이다....
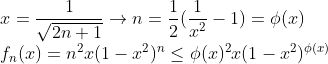
즉 x가 고정되면, n=phi(x)일 때, f_n(x)가 최대가 되고, 이 값은 x가 고정되어 있으면 그냥 상수이기 때문에 bounded...
그래프에서 각 파란 점이 그냥 잠깐 올라갔다 내려온다는 것을 생각하면 된다.
2. Uniformly Bounded
그러나 아마 9-1의 그래프에서 보았듯이, n이 커짐에 따라 무한대로 값이 튀어버리기 때문에, 모든 f_n이 M보다 작다는 불가능하다...
이와 관련된 몇가지 성질들을 살펴보자.
1. (Pointwise Bounded and Convergence)
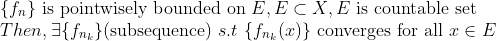
위에서의 수렴성은 당연히 Pointwise를 말하는 것! (각각의 x)
증명까지 갈 것은 없을 것 같고, 설명으로 대체한다.
1. x1를 고정시켜 놓으면 -> {f_n(x1)}는 Bounded Sequence in (Real or Complex Plane)이라서, 유클리드 공간에서 Bounded 공간에 무한개의 점을 찍으면, limit point가 생기고, 즉, x1에서 수렴하는 subsequence를 잡을 수 있다.
2. 그런데 E가 Countable set이므로, 그런 각 x를 셀 수 있을 것이다. (x1, x2, x3, ....)
이 때, x2에서 부분수열을 잡을 때에는 x1에서 나온 함수들로만 다시 subsequence를 잡는다!
x3에서 부분수열을 잡을 때에는 x2에서 나온 함수들로만 다시 subsequence를 잡는다! -> 반복....
3. 이러한 부분수열을 다 잡고 난 후, 또 새로운 부분수열 하나를 잡는데,
-> x1에서 첫번째 나온 함수, x2에서 두번째 나온 함수, x3에서 세번째 나온 함수...... -> {g_n}이라고 하자.
그러면, {g_n}은 어떤 x_n에서도, x_n에서 뽑은 부분수열이 될 것이다.
if x1의 경우 -> 모든 g_n은 결국엔 x1에서 뽑은 부분수열임....
if x2의 경우 -> 모든 g_n (n>1)은 결국 x2에서 뽑은 부분수열....
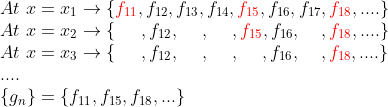
4. 즉, g_n은 어느 x_n에서나 수렴할 것이다!
여기서 왜 Countable set으로 잡았는가? -> 다음 성질을 보면 알 수 있다.
2. (Uniformly Bounded and Convergence)
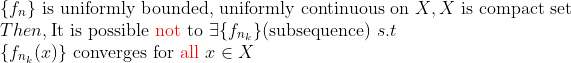
만일 X가 Compact set이라면(즉, Uncountable...)이면, 심지어 Uniformly Bounded, Continuous임에도 불구하고,
수렴하는 부분수열조차도 못 잡을수도 있다는 말이다... (Pointwise 수렴도 불가능하다...)
예시를 하나 들어보자.
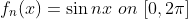
그러면 Uniformly bounded이다.
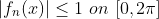
그런데, 만약에 어떤 부분수열이 수렴한다고 가정하자.

그러면 다음과 같은 식이 성립한다.
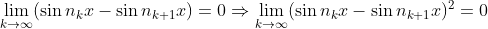
그런데,
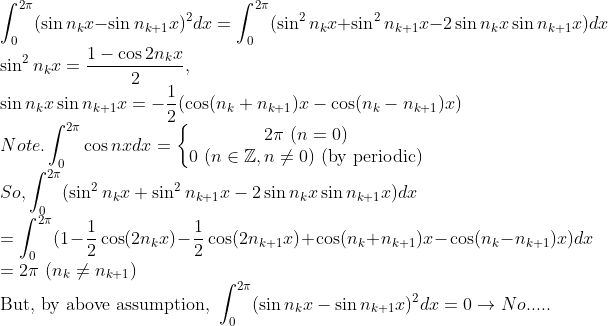
그러므로, 위의 가정은 틀렸으므로, 저렇게 수렴하는 부분수열은 없다.
그렇다면, 1번하고 어떤 차이가 나길래 이런 일이 발생했을까???
-> f_n이 연속이고, X가 Compact 라는 것이 문제이다...
1번에서는 그냥 x를 각각 잡을 수 있어서 상관이 없는데, 여기서는 x를 고정시키면 연속조건에 의해서 locally x 주변까지 영향을 주기 때문에, 또 X가 compact라서 locally 영향이 전체에 영향을 주고,... 즉 X 전체가 Coupling 되어있는 느낌이다...
이러한 문제를 해결하기 위해서, Uniformly Continuous에서 더 나아간 Equicontinuous가 등장한다!
이번에는 동등연속(Equicontinuous)에 대한 내용을 살펴보자.
여기서 Family(족)라는 용어가 나오는데, 그냥 집합이라고 생각하면 된다.
(Equicontinuous)(동등연속)
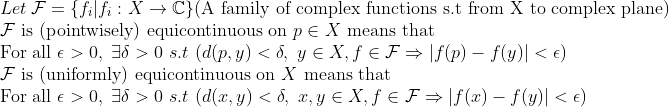
즉, 연속(혹은, 균등연속)조건이 같은 delta에 대해서 F의 모든 원소(member)에 다 적용이 되는 것이라고 생각하면 된다.
특히, 여기서는 따로 언급하지 않으면 Uniformly Equicontinuous의 경우를 Equicontinuous라고 부를 것이다!
(NOTE)
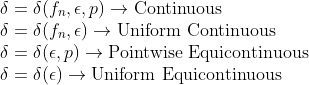
Equicontinuous이면 당연히 F의 모든 원소가 Uniformly Continuous일 것이다.
그러나 역은 성립하지 않는다... 왜냐면 delta가 각각의 f_n에 의존하기 때문이다! -> 아래의 성질 참고!
(그 중에 어떤 delta를 써야 모든 f에 성립할지는 모른다....)
그림을 통해서 비교하면
1. Uniformly Continuous
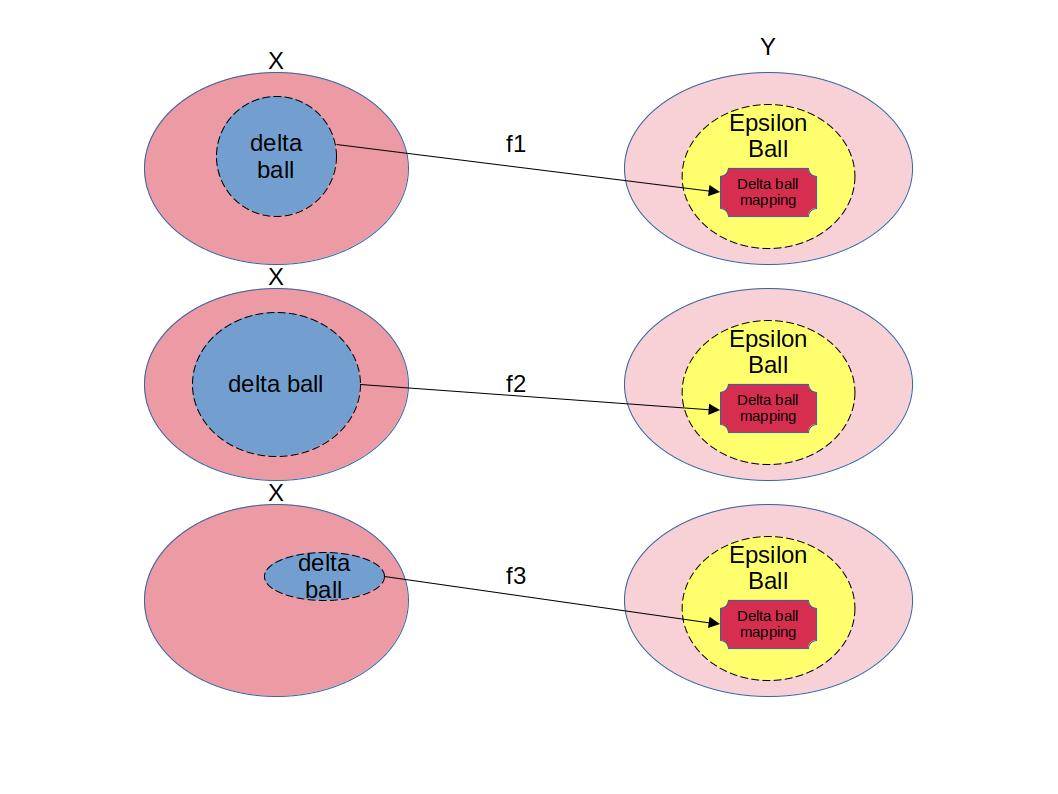
2. Equicontinuous(Uniformly)
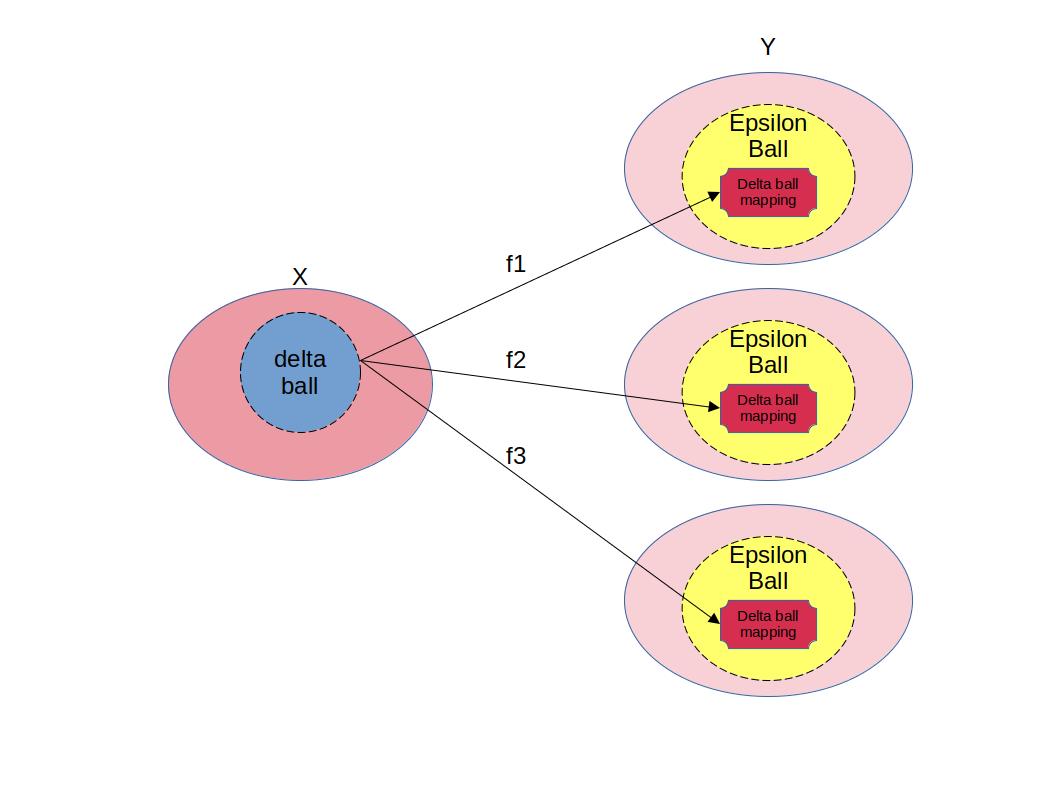
Equicontinuous와 관련된 성질을 살펴보면,
(Uniform Convergence -> Equicontinuous)
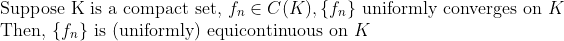
(증명)
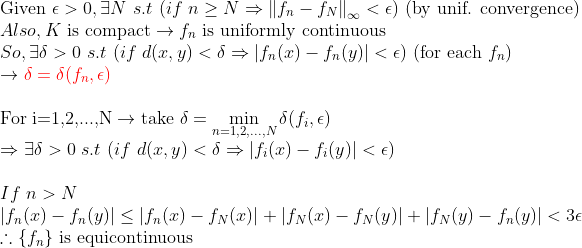
여기서 조심해야 할 것은 Uniformly Continuous에선 delta가 각 f_n에 따라서 변한다는 것이다!
그러므로, 이런 논리는 안된다.
(모든 n에 대해서 f_n이 Uniformly Continuous이니... 당연히 Equicontinuous 아닌가???)
또한, 위 성질의 역은...
(Equicontinuous and Compact)
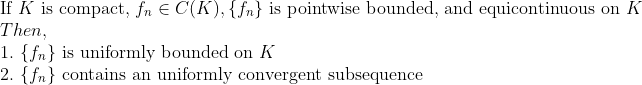
위에서는 Uniformly Bounded이고 Uniformly Continuous임에도 불구하고, 수렴성을 보장을 못했는데,
Equicontinuous에서는 Pointwise bounded -> Uniformly bounded가 되고, 더 중요한 것은 수렴성을 보장할 수가 있다!!!
(증명)
1.
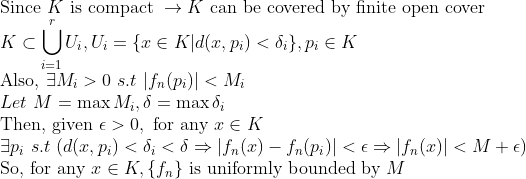
2.
여기서 Compact set이 Countable Dense subset을 가진다는 것은 다음 챕터(부록)에서 다룰 것이다!

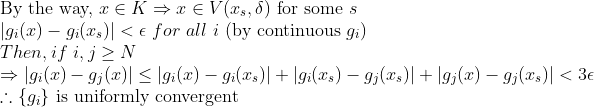
Compact set K가 Countable dense subset을 가진다는 것과
f_n이 Countable subset에서 수렴하는 부분수열을 가진다는 것을 이용하였다!
오늘 내용을 정리하자면...
먼저, Compact set K에서!
1. 기존의 Uniformly Continuous...
Uniformly Bounded, Uniformly Continuous는 함수열의 수렴성을 보장"도" 못한다...
(즉, "유클리드 공간에서 Bounded -> 수렴하는 부분수열 고를 수 있다..." 가 여기서는 연속성에 의해 통하지 않는다!)
2. 그래서 Equicontinuous를 도입!
-> Uniformly Convergence이면 Equicontinuous!
-> (역으로) Equicontinuous이면 Uniformly Convergence!
문제는, 이 Equicontinuous를 만족시키기가 꽤나 까다롭다는 것이다... (Uniformly Continuous도 꽤나 빡빡한 조건이었다는 것을 상기하면...)
뭐... 일단 넘어가도록 하고, 다음챕터에서는 위의 증명에서 생략한 부분을 살펴보고(Topology에 대한 내용!)
Stone-Weierstrass 정리로 넘어가도록 하자..



