미적분학에서 다변수함수의 미적분, 특히 편미분을 다루면서 편미분 순서 바꾸는 것을 보았을 것이다... 미분의 정의를 생각해보면, 이는 결국 lim 순서를 바꾸는 것이다. 그 때는 미분의 정의를 이용해서 다 펼쳐서 생각했는데, 일반적으로 아무 생각없이 lim 순서를 바꾸는 것이 괜찮은 것일까???
다음의 예시로 시작해보자...
1. LIMIT 순서

이 예시만 보아도 알 듯, 순서를 바꿔놨더니 결과가 달라진다. 다음 예시들도 다 순서에 따라 결과가 바뀐다....
2. 함수열의 연속
연속도 Limit로 볼 수 있다!

3. 함수열의 적분가능성

4. 함수열의 적분값

5. 함수열의 미분

이런식으로, limit 순서 바꾸는 문제가 해결이 안되니, 연속, 미적분까지 문제가 생겨버린다....
이를 해결할 수 있는 것이 바로 Uniform Convergence이다! 이번 챕터에서는 이를 알아볼 것이다!
예시 순서대로 Uniform Convergence가 문제들을 해결해줄 수 있는지 확인해보자.
1. limit 순서 바꾸기, 함수열의 연속
1번의 경우는 2번의 경우에서 그냥 x를 무한대로 보낸것이라고 생각할 수 있으므로 더 일반적인 함수열의 연속을 확인해보자!
(Continuity of Seq of Functions)

즉, 모든 f_n에서 t=x에서 연속이고, Uniformly Converge이면 f가 t=x에서 연속이다!
(증명)

지금까지 배운 내용들을 잘 정리하면 증명하는데 어렵지는 않을 것이다!(unif. convergence, convergence, continuous)
(Corollary)

그러면 역은 성립할까?
즉, f가 연속이고, f_n이 모두 연속이면 -> Uniformly Convergent???
답은 아니다.... 그러나, Compact set에선 축소구간정리를 이용하면 가능할 수 있다!
(Continuity of Seq of Functions (Reverse))

(증명)

설명을 하자면
1. K_n이 Closed set인 이유는
(연속함수의 역상이 Open/Closed를 보존한다고 하였다...
-> K_n의 조건은 y>=epsilon, 즉 [epsilon,inf)이므로 이 구간은 Closed set이다.
-> 그러므로 연속함수의 역상인 K_n은 Closed!)
2. K_n이 compact인 이유는 K_n이 closed subset of (compact set K)이기 때문이다!
3. {K_n}에서 축소구간정리처럼 하려고 했는데, 모든 x에서 epsilon보다 작아지는 n을 구할 수 있다... 즉, x가 K_n의 원소가 될 수 없다! 이는 모든 x에 대해서 성립하므로 결국 모든 x는 K_n들의 교집합에 들어갈 수 없다. 즉, K_n은 empty set이다!
축소구간정리에서는 항상 원소가 존재했었는데...??? -> 그렇다면, 가정이 틀린 것이다!(K_n이 모두 nonempty set인 가정이 있었다!) -> 어떤 K_n이 empty가 된다!!!
그러므로 모든 x에 대해서 g_n(x)<epsilon이 되는 n이 존재하므로, uniform convergence를 만족한다!
증명을 보면 알겠지만, 우리가 배웠던 Topology를 많이 쓴다... 다시 한번 기억하자!
더 나아가서, 연속함수공간의 Completedness에 대해서 확인해보자!
먼저 Function Space(함수공간)에 대해서 조금 설명한다.
(Function Space)
A set of Functions with the same Domain and Codomain
거창하게 보이지만, 그냥 같은 정의역과 공역(not 치역)을 가진 함수들의 집합이다.
예를 들어서 metric space X에 대해서 다음과 같이 표현한다.
1. X에서 연속인 함수들의 집합 (공역은 대부분 복소수로 생각한다.)

예를 들어, [0,1]에서 연속인 함수들의 집합이라면...

2. X에서 n급 함수(n번 미분가능하고, 그 결과가 연속인 함수)들의 집합

3. X에서 무한번 미분가능한 함수들의 집합

4. [a,b]에서 alpha에 대해서 리만-스틸체스 적분이 가능한 함수들의 집합

이런 식으로 표현한다...
Metric space X에서 이미 Norm이 정의되어 있다는 것을 생각하자!
특히, 우리가 주목할 Function Space는 C(X)이다. 우리가 여기서 쓸 Norm은 다음과 같다.
(Supremum Norm (L-Infinity Norm))

(NOTE)
(Note 1)
1. 적분파트 8-5에서 본 2-norm, p-norm의 확장판! -> 그 때의 정의에서 p를 무한대로 보내면 위의 norm을 얻을 수 있다.
2. Uniform Convergence는 L-Infinity Norm을 사용한 수렴성이다!
(Note 2)
기계학습(Machine Learning) -> 신경망구조(NN)에서 우리의 목표는 어떤 행동을 도출해내는 layer 구조를 만들어 내는 것이라고 할 수 있다. 각 layer마다 변수가 있으니, 결국
Loss Function을 최소로 해주는, 함수(layer 구조) f를 만드는 것이라고 생각을 할 수 있다.
일반적으로 Loss Function에는 l2-norm을 이용해서 Gradient Descent를 이용해서 f를 추정(Regression)하지만,
이 Uniform Convergence 관점으로 보면
-> L2-norm은 (f의 뾰족뾰족한 locally minimum)을 그닥 잘 쫓아갈 수가 없다... (목표함수와 지금 가지고 있는 함수 사이의 면적을 나타내기 때문에, 뾰족해지면 그 뾰족한 느낌을 따라가기 어렵다고 생각할 수 있다.)
-> L-infinity norm은 그에 반해서 Sup(Max)를 줄이면서 가기 때문에, 전체적으로 저 뾰족한 곳도 잘 따라갈 것이다.
다만, 수렴속도가 L2-norm에 비해서 늦을 것이고, 저 sup(max) 때문에 연산속도 자체가 전체적으로 느려질 가능성이 있다!
--> 그래서 초반에는 L2-norm을 이용해서 대강 빠르게 따라가고, 후반수렴에는 L-inf norm을 이용하면 세세한 부분들도 잘 따라가게 할 수 있을 것이다! (실제로, 여러 논문들에서 이런 식으로 하던게 기억이 남....)
C(X)에서 Unbounded Function은 생각하지 않는다! (사실, X가 compact라면, 자동으로 성립된다!)
즉, 여기서 우리가 다룰 C(X)는 복소수값을 뱉는, Bounded, Continuous 함수의 집합이라고 생각하면 된다.
(Completedness of Continuous Ftn Space)
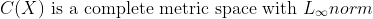
(증명)

이미 X에서 코시수열이면 수렴한다는 것을 알고 있고, 이 수렴하는 f가 C(X)의 원소인지 확인만 하면 된다!
이 C(X)에서 쓰는 Notation 몇 개를 짚고 넘어가자!
(Notation)
1. Uniformly Closed
Closed Subset of C(X)
2. Unifrom Closure
Closure of a set A in C(X)
자, 이번시간에는 Uniform Convergence와 연속성(Continuity)에 관해서 알아보았고,
다음시간에는 이번에 못한 Uniform Convergence와 미적분에 관해서 알아본다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 10-1. 연속 종류가 왜 이렇게 많은지... (Uniform Boundedness, Equicontinuous) (0) | 2023.02.26 |
|---|---|
| (해석학) 9-3. lim와 적분 순서를 바꿔보자! (Uniform Convergence -> Integral/Differentiation) (0) | 2023.02.23 |
| (해석학) 9-1. 수열의 원소를 Number에서 함수로 확장하면? (Uniform Convergence) (0) | 2023.02.22 |
| (해석학) Summary 2. 수열부터 적분까지 (0) | 2023.02.21 |
| (해석학) 8-5. 아직 좀 부족한데....? (Improper Integral, Space of Riemann-Integrable ftns) (0) | 2023.02.21 |



