이번 챕터에서는 COMPACT SET의 개념과 성질에 대해서 알아본다.
아마, 해석학 초반에 가장 장벽이 높은 개념이 아닐까 싶은데 그만큼 중요하기 때문에 어쩔 수 없다... 확실하게 알고 넘어가야 뒤에 나올 내용들을 이해할 수 있다.
먼저, compact set이 무엇인지 살펴보기 전에 몇가지 용어들을 살펴보자.
(Open Cover)
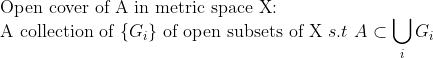
즉, A의 open cover라는 것은
A를 덮는 X의 open subset들의 모음(collection)이라는 뜻이다.
예를 들어서, (-1,1)의 open cover에는,
1. {(-2,2)} 도 있을 수 있고,
2. {(-1,0), (-1,2)} 도 있을 수 있고,
3. {(-1,-0.3),(-0.4,0),(-0.1,2)} 도 있을 수 있고... 여러 방법이 가능할 것이다.
여기까지 이해되었다면, compact set의 정의를 보자.
(Compact Set)
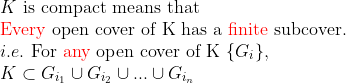
즉, K가 compact하다는 말은
K의 모든 open cover에서 유한개의 원소(open subset)로 K를 덮을 수 있다는 이야기이다.
이해를 돕기 위해서 예를 들어보자.
1.

K를 덮는 open cover는 (-2,2)가 있으니, 1개로 덮이니까 K는 compact이다. 라고 생각하면 안된다!
위의 정의에서 모든 open cover라는 내용이 중요하다...
즉, open cover를 내가 어떻게 잡던지 간에, 유한개로 K가 덮일 수 있어야 한다.
그렇다면, 어떻게 compact인지 아닌지 확인할 수 있을까?
먼저, 0을 덮는 open set을 생각해보자. 정의에 의해 그 open set 안에 open ball이 포함되어야 할 것이므로,
어떤 반지름 r에 대해서 (-r,r)로 0을 덮을 수 있을 것이다.
그런데, 이 r이 주어짐에 따라서, 우리는 덮을 원소를

인 경우만 살피면 된다. 왜냐하면, n이 1/r보다 크면 0을 덮는 open set에 포함이 되기 때문이다....
그러니, 결국에 기껏해야 [1/r]개의 open set으로 나머지 원소들을 덮을 수 있다.
그러므로 저 K는 유한개의 open subcover로 덮을 수 있으므로 compact set이다.

2.
K=(0,1)
이번에도 (0,1)이 K를 덮으니까 K가 compact하다고 하면 절대 안된다!
이번엔 다음과 같은 open cover를 생각하자.
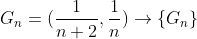
이게 K를 덮는지 확인해보자.
(여기서 본능적으로 덮일 것 같다고 생각하는 건 조금 위험할 수 있다... 실수축이라 그렇지 복잡한 metric space로 가면 문제가 생길수도 있다. -> 집합관계를 통해서 확인해야 한다.)

문제는 여기서 이 G_i들 중 하나라도 빠지면, K를 덮지 못한다는 것이다.

그러므로, 이 open cover는 K를 덮을 수 있는 finite subcover가 존재하지 않는다.
그러므로 K는 compact가 아니다!
3. 후에 증명할 것이지만, K=[0,1]은 compact하다.
2번과 비교하면 (0,1)이 [0,1]에 포함된다고 compact하지는 않다!
즉, Compact set이라는 거는 덮는 거야 어떻게 덮든 간에,
잘만 추려내면 항상 유한개의 open set으로 덮어질 수 있다는 것을 말한다.
위의 예시를 보고, 꼭 이해하고 다음의 내용을 진행하기를 바란다.
지금부터는 compact set의 성질에 대해서 살펴볼 것이다.
앞 챕터에서 Open set의 상대적인 개념을 보았던 것처럼, compact의 경우에도 상대적인 개념을 생각할 수 있다. -> 정의에서 X 대신에 Y를 쓴다고 생각해보자...
그러나, 다음 성질에 의해서 compact의 경우, 상대적인 개념을 무시할 수 있다.
(Compact Relative to....)

(증명)
1. X에서 compact -> Y에서 compact

K를 덮기 위해 무한개의 open set으로 일단 덮어버린 다음 (무한개도 가능하고, open set의 크기도 자유자재로 잡을 수 있으니 어떻게든 덮이긴 할 것이다), open set의 상대적 성질에 따라서 X에서 본 후, compact 성질에 따라서 X에서는 유한개로 걷어낼 수 있으므로, Y에서도 유한개로 덮어진다는 말이다.
즉, open cover를 아무렇게나 잡은 다음에 잘 추려내면 Y에서도 유한개로 덮일 수 있으므로, Y에서 compact하다고 할 수 있을 것이다.
2. Y에서 compact -> X에서 compact
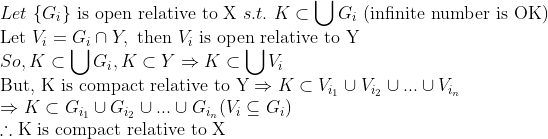
역의 경우에도 앞과 동일하다.
다음 볼 성질은 아주 중요한 성질로, Closed set과 Compact set 사이의 관계이다.
(Closed Set & Compact Set)
1. Compact set은 Closed set이다! (역은 성립하지 않는다 -> 하이네-보렐 정리 참고)
2. Compact set의 Closed subset은 Compact set이다!
(증명)
1.
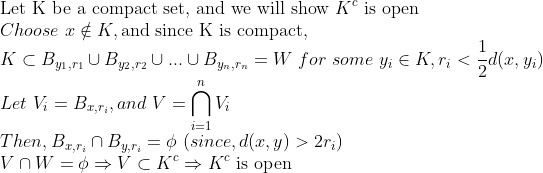
그림을 통해서 살펴보면 다음과 같다.
빨간 원이 K이고, 파란 원이 B_{y,r}, 녹색 원이 B_{x,r}이라고 생각하면 된다.
파란 원의 합집합은 녹색원의 교집합과 만나지 않는다!

2.

F의 open cover를 마음대로 잡고 그 open cover에 F의 여집합을 추가하면, K도 덮기 때문에, 그 open cover에서 K를 덮는 finite subcover를 뽑아낼 수 있다. 이 때, F의 여집합이 그 subcover에 포함되어 있다면, 빼주자.
그럼 F의 여집합이 빠진 subcover는 F를 finite하게 덮게 된다.
-> 정리하면, F의 open cover를 어떻게든 잡아도, 잘 추려내면 F를 덮는 finite subcover를 잡아줄 수 있으므로, F는 compact이다.
(Corollary)
만일, F가 closed set이고, K가 compact라면, 그 교집합은 compact이다.
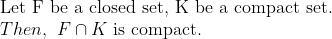
자, 여기까지 잘 따라왔으면, 다시 한번 리마인드해보자!
다음 챕터부터는 이를 이용한 중요한 정리들인 Nested Interval Theorem(축소구간정리)와 Heine-Borel Theorem(하이네-보렐정리), Bolzano-Weierstrass Theorem(볼차노-바이어슈트라스 정리) 등을 살펴볼 것이다.



