이번 챕터에서는 기본적인 집합 내용에 관해서 다룰 것이다.
들어가기 전에 먼저 용어 정리부터 하고 들어간다.
(Function(함수))
f : A -> B => f is a function from A to B / mapping of A into B

가 정의 되어있을 때,
A : Domain of f(정의역)
f(A): Range of f(치역)
B : Codomain of f(공역)
만일 X가 A의 부분집합인 경우,
f(X): the image(상) of X under f
또한, preimage(역상)을 정의하는데,

Y의 원소에서 A 원소에 하나씩 대응될 필요는 없다.
(만일, f(1)=2, f(2)=2 이면, f^{-1}(2)={1,2} 이다.)
여기서 주목해야 할 것은,
함수는 모든 A의 원소에선 B의 어느 원소에 대응이 되어야 하고, 그러나
모든 B의 원소에서 A에 대응될 필요는 없다. (공역과 치역은 다를 수 있다.)
또한, 대응되는 B가 중복될 수도 있다. 여기서 나오는 용어들이 바로 surjective, injective, bijective function(mapping)이다.
1. Surjective Function(전사 함수) -> Onto
공역과 치역이 같다.


2. Injective Function(단사함수) -> 1 to 1 mapping (1대1 함수)
대응될 때, 중복되는 B 원소가 없다. -> B의 각 원소의 preimage의 원소 개수가 기껏해야(at most) 1개
(B를 잘 줄이면 역함수 존재)


3. Bijective Function(전단사함수) -> 1 to 1 correspondence(1대1 대응), 1 to 1 mapping A onto B
Surjective, Injective Function을 동시에 만족하는 Function -> 역함수가 존재한다.
워낙에 간단한 내용들이라 잘 알거라고 생각한다.
또한, 다음과 같은 성질들을 알고 있자. 많이 유용하다.

1번의 경우 injective의 경우를 생각하자. Y가 B를 갖고 있으면, 왼쪽 항의 결과는 B를 가지지 못한다.
surjective인 경우에는 둘이 동일하다.
2번의 경우 surjective의 경우를 생각하자. X가 1, 2라면 f(X)는 A,B, preimage는 1,2,3이 될 것이다.
injective인 경우, 둘이 동일하다.
이번에는 집합(Set)에 대해서 약간 더 알아보자. 너무 기초적인건 패스하고, 헷갈릴만한 무한집합 개념에 대해서 보자.
1. Finite Set(유한집합)
집합의 원소의 개수가 유한개인 경우
2. Infinite Set(무한집합)
집합의 원소의 개수가 무한개인 경우
3. Countable Set(셀 수 있는 집합) -> 유한집합과 다르다!!
집합의 원소의 개수를 셀 수 있는 경우(카운트할 수 있는 경우) -> 자연수집합과 대응시킬 수 있는 집합
(예시)
a. 유한집합 -> 당연!
b. 자연수집합 -> 1,2,3,.... 이런식으로 순서대로 셀 수 있다.
c. 유리수집합 -> 분모를 1,2,3,4,.... 이런 식으로 늘려가고 분모가 n일 때, 분자를 1,2,3,....,n-1 이런식으로 줄세워서 셀 수 있다.
-> (1/2), (1/3, 2/3), (1/4,2/4,3/4), (1/5,2/5,....),.... (약분으로 인한 중복은 추후에 하나씩 빼면 된다.)

4. Uncountable Set(셀 수 없는 집합) -> 무한집합과 다르다!!
countable set이 아닌 경우, 즉, 집합의 원소의 개수를 헤아릴 수 없는 경우 -> 자연수 집합과 대응시킬 수 없다.
(예시)
a. 실수집합 -> 증명을 하겠지만 위의 유리수집합처럼 세는 방법이 딱히 없다....
b. 닫힌구간 [a,b]
유한집합과 무한집합은 우리가 아는 딱 그대로로 생각하면 되고, countable / uncountable set은 개인적으로는 마음에 썩 들지 않는 번역이긴 한데, 영어에서 uncountable과 countless는 다르다는 것을 생각하면 된다.
Countless는 "셀 수 없을 정도로 많은" 이라는 뜻이고, uncountable은 정말로 "카운트가 불가능하다(unable)"는 뜻으로 해석하자.
(NOTE)
Countable set의 모든 부분집합(subset)은 Countable하다. (유리수집합 세는 것을 생각하면 된다!)
이 말을 거꾸로 한다면, Countable set들의 합집합이 Countable하다는 것을 이야기한다. 즉,
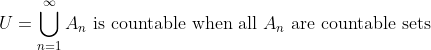
(잠깐!!!) 위에서는 부분집합이 countable한 개수인 경우인데 (n=1,2,3,...) 만일, 부분집합의 개수가 uncountable이라면???
-> 예를 들어서 다음과 같이 표현할 수 있다!
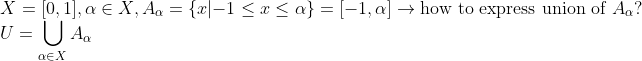
사실, countable set은 직관적이기도 해서, 별로 어려움이 없지만,
저 uncountable set이 꽤 추상적이라 애를 먹을텐데, 실수가 uncountable이라는 사실을 증명하면서 연습해보자.
먼저, 이를 증명하기 위해서 수열의 정의를 보고 넘어가자.
(Sequence(수열))
자연수집합을 정의역으로 갖는 함수. 즉, 다음을 그냥 수열이라고 부른다.
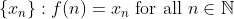
(Lemma)
0과 1로 이루어진 수열들의 집합 A는 uncountable set이다.
(증명)
A의 countable 부분집합을 잡아서 이것이 진부분집합이라는 것을 보이면 된다.
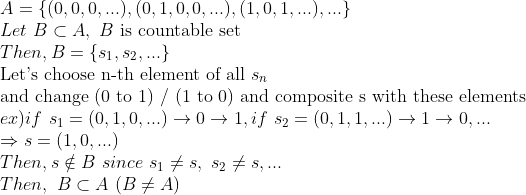

각 수열들을 2진수로 대응을 시킨다면,
(예를 들어서 s=(0,1,0,0,1,1,...) -> 0.010011....(2) 라고 한다면),
A는 0과 1사이에 있는 모든 2진수를 다 표현한 것의 집합이다.
각 2진수는 실수에 다 대응이 되기 때문에, 닫힌 구간 [0,1]은 uncountable set이고, 이를 포함한 실수집합도 uncountable set이 된다. (당연히 uncountable set을 포함한 집합은 uncountable set일 것이다!)
여기까지 countable set과 uncountable set에 관한 내용을 정리하였다.
다음 챕터에서는 드디어 OPEN SET과 CLOSED SET에 관한 내용을 정리할 것이다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 2-3. 열린 집합과 닫힌 집합의 성질(Property of Open / Closed set) (0) | 2023.02.05 |
|---|---|
| (해석학) 2-2. 거리 개념과 집합 (Basic Set Theory - Concept of Open / Closed Set) (0) | 2023.02.03 |
| (해석학) 1-2. 차원 확장! 복소수와 유클리드 공간 (Complex Field, Euclidean Space) (0) | 2023.01.31 |
| (해석학) 1-1. 도대체 뭐가 문제라 증명을 못했을까? (What is Real Number?) (2) | 2023.01.31 |
| (해석학) 해석학 개요 (0) | 2023.01.02 |



