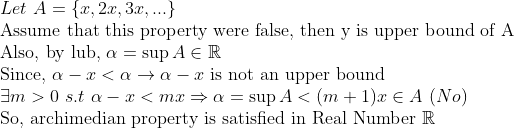아마 여기까지 찾아본다면 고등학교에서 증명하지 않는 정리를 어떻게 증명할까...? 라는 질문을 가진 사람들과
미적분학에서도 증명하지 않는, 혹은 뭔가 애매하게 넘어간 정리들을 좀 확실히 알고 싶은 사람들이 대부분일 것이라고 생각한다. 이러한 질문에서 Topology에 대한 논의를 시작해볼 것이다.
결론적으로 증명을 못했던, 아니면 뭔가가 찝찝하게 넘어간 이유는 Topology 때문이다.
더 자세하게 얘기하면 Topology를 통한 실수의 성질들을 짚고 넘어가야 하는데 뒷 내용을 보면 알겠지만 만만치는 않은 내용들이다. 그러나 여기에 나오는 내용들(Topology)을 알면 공대 기준 대학원 가서도 유용하게 써먹기 때문에 한번 알면 좋긴 하다.
일단 Topology(위상)가 무엇인지 살펴보자.
간략히 설명하자면 "공간"에 대한 학문이라고 할 수 있다. 추상적인 내용이지만 우리가 살고 있는 공간(직교 좌표계의 공간)을 넘어서 집합도 일종의 공간으로 볼 수도 있다. 여기서 특히 주목하는 건, Metric이 정의된 공간을 주목하게 되는데, Metric에 대해선 뒤에서 설명하도록 한다. 그렇다면, 일단 집합에 대해서 조금 더 알아보자. 특히 이를 통해서 "실수(Real Number)"의 unique한 성질에 대해서 살펴보도록 하자.
기본적인 집합에 대한 성질은 다 안다고 생각하고 설명한다.
1. (Ordered Set) -> 집합론 참고!
Ordered Set이란 Order(순서)가 정의된 집합을 말한다.
여기서 Order란,
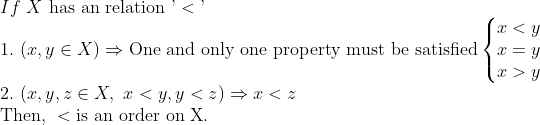
즉, 1,2번 성질을 만족하는 관계(relation)(혹은 연산이라고 생각할수도!)가 바로 order가 된다.
사실 실수에서는 당연히 부등호가 order이다.
너무나 당연한 얘기라고 생각할 수 있지만, 복소수에서는 이러한 관계를 만들어 낼 수가 없다. (물론 정확히 따지자면, 복소수체가 순서체가 아닌 것이다.) 여기선 일단 복소수에서 대소관계를 따지지 않았다는 것을 생각하면 될 것이다...
이 Ordered Set에서는 (유계(bounded))를 정의할 수 있다.
(1) Upper bound(상계) -> bounded above(위로 유계)
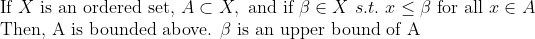
그러니까, 개념 상으로, A가 무한히 커지지 않는다는 것을 말한다. (beta가 A의 어느 원소보다 크거나 같다.)
uppere bound 값은 당연히 하나가 아니다...
ex) A=[-inf,1) -> beta=2,3,1000,....
같은 방법으로 lower bound(하계), bounded below(아래로 유계)도 정의한다. (무한히 작아지지 않는다.)
(2) Least Upper Bound(최소상계) -> sup
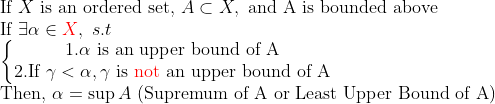
즉, supremum이라는 것은
간단하게는, A의 최댓값처럼 생각하면 되는데 만일 최댓값이 존재하지 않는다면(열린 구간), 마치 닫힌 구간처럼 생각해서 최댓값을 뽑아내면 된다.
물론, 정확히는 sup A의 뜻은 A의 상계 중에서 최솟값을 말한다.
같은 방법으로, 최대하계(gratest lower bound, infimum -> inf A)도 정의한다.
여기서 한가지 참고할것은, sup이나 inf는 굳이 A의 원소가 아니어도 된다는 것이다. (X의 원소면 됨)
ex) sup[-1,1-1/n) = 1
(3) Least-upper-bound(lub) Property
위에서는 sup A가 X의 원소였다. 이 때, A가 공집합이 아니면 least-upper-bound(lub) Property를 가진다고 한다.
그런데...? -> sup A를 구해보았더니 X의 원소가 아니면..? lub Property를 가지지 않는다고 한다.
아마 뭔 얘기인가 싶을 수도 있는데, 예시를 하나 들어보자.
(ex) 다음과 같은 상황을 생각해보자. -> X가 실수가 아니라 유리수라고 생각하자.

오직 유리수 안에서만 생각해보자. 그러면 유리수 안에서 sup A를 만들어 낼 수 있을까???
실수로 확장해서 생각해보면 안된다는 것을 바로 알 수 있다. 즉, sqrt(2)를 정의할 수 없기 때문에, A의 upper bound가 열린 집합으로 잡히게 된다. (나중에 open set, closed set을 보고 와서 한번 다시 보자!)
그러니, upper bound들의 set에서 최솟값을 구할 수가 없어진다...
이 말을 약간 다르게 하면, 실수에서는 항상 저 upper bound들의 set이 닫힌 집합으로 잡히므로, 최솟값을 항상 구할 수 있고, sup, inf가 항상 존재한다는 이야기가 된다!
(4) lub property와 완비성(Completedness)
위의 예시에서 나온 얘기를 정리해보면,
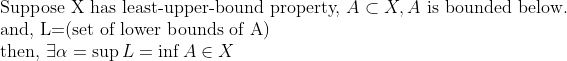
그림으로 나타낸다면 다음과 같이 될 것이다.

(증명)
처음보면 약간 혼동이 있을 수 있는데, 차근차근 보면서 따라가보자!

이 성질이 무엇을 의미하는가??
만일, 위던지 아래던지 유계인 집합 A가 있는데 그렇다면 (set of (upper or lower) bound of A) = L을 잡을 수 있다. 그러면 집합 X는 A와 L로 분할이 될 것이다. 이 때, lub 성질에 의해 A와 L의 경계에 있는 값이 X에 속한다.
즉, X를 어떻게 쪼개든 간에, 그 사이에는 X 밖에 있는 원소가 잡히지 않는다. -> 완비성(Completedness)을 이야기 한다.
예시를 들어보자..
(3)의 예시에서는 유리수가 lub 성질을 만족하지 못하므로, 완비성을 만족하지 않는다.
즉,
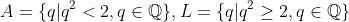
인 경우 lub 성질을 만족하지 않으므로, sup A가 유리수가 아니다. 즉, 유리수 사이에 유리수가 아닌 것(유리수가 아닌 실수)이 존재한다...
그러나, 실수의 경우, 저런 식으로 쪼개도 경계값은 항상 실수가 나온다. 이를 실수의 완비성(Completedness of Real Number)이라고 한다. 그리고, 이 완비성이 실수의 독특한 성질 중의 하나이다.
2. Field(체) -> 추상대수학 참고!!
체(Field)라는 것은 간단히 말하자면, 덧셈과 곱셈이 잘 정의된 집합을 이야기한다. 즉, 사칙연산이 잘 정의된 집합을 얘기한다.
정확히 이야기하면, 체 F란 다음을 만족하는 집합을 이야기한다.
(1) 덧셈에 대한 axioms
a. 덧셈에 대해서 닫혀있다.

b. 덧셈에 대해서 교환법칙이 성립한다.
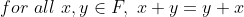
c. 덧셈에 대해서 결합법칙이 성립한다.

d. 모든 원소에 대해 항등원 a가 F 안에 존재한다.
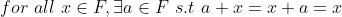
e. F의 각 원소 x에 대해 역원 b(x)가 F 안에 존재한다.

(여기서는 혼동을 줄이기 위해서, 항등원과 역원을 a와 b(x)라고 했지만, 이미 알고 있듯이, a=0, b(x)=-x이다.
항등원은 모든 원소에 대해서 동일해야 하고, 역원은 x에 따라서 바뀔 수 있다.)
(2) 곱셈에 대한 axioms
a. 곱셈에 대해서 닫혀있다.
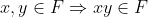
b. 곱셈에 대해서 교환법칙이 성립한다.
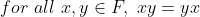
c. 곱셈에 대해서 결합법칙이 성립한다.

d. 모든 원소에 대해 항등원 a이 F 안에 존재한다.
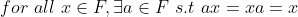
e. F의 각 원소 x에 대해 역원 b(x)가 F 안에 존재한다. (단, x=0은 제외)
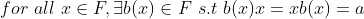
(여기서도 혼동을 줄이기 위해서, 항등원과 역원을 a와 b(x)라고 했지만, 이미 알고 있듯이, a=1, b(x)=(1/x)이다.)
(3) 덧셈과 곱셈에 대해 결합법칙이 성립한다.
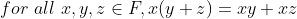
(ex)
자연수 집합은 체가 아니다! -> 덧셈과 곱셈에 대한 역원이 자연수 집합에 존재하지 않는다.
정수집합 또한 체가 아니다! -> 곱셈에 대한 역원이 정수에 존재하지 않는다.
유리수 집합은 체이다! -> 덧셈과 곱셈에 대한 역원이 유리수에 존재
또한, 위의 order set과 연관지어서 Ordered Field(순서체)를 정의한다.
(Ordered Field)(순서체)
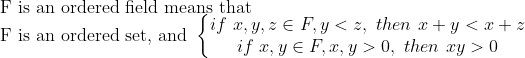
자, 여기서는 따로 실수의 정의를 소개하는 시간이 아니라 넘어가지만, 여기서의 결론은!
실수(Real Number)는 Complete Ordered Field 그 자체이다!
유리수체로부터 실수체를 구성하면 나오는 결론이다. 여기서 더 나아가고 싶은 사람은 집합론을 참고하자! (추후에 작성예정)
실수의 완비성을 이용해서 실수의 성질에 대해서 더 나아가보자!
(Archimedian Property in Real Number)(아르키메데스 성질)
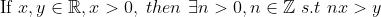
(증명)
이는 실수가 아무리 작아도 상수배에 의해서 어느 실수보다 커질 수 있다는 것을 뜻한다.
(Corollary 1)
두 실수 사이에는 언제나 유리수가 존재한다.

(증명)

여기서 nx가 당연히 정수 m에 대해서 m-1과 m 사이에 있겠지... 라고 생각하면 된다.
(Corollary 2)
0보다 큰 실수의 nth-root는 0보다 큰 실수에 존재하고, 유일하다. 즉,

(증명)
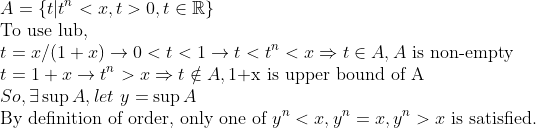
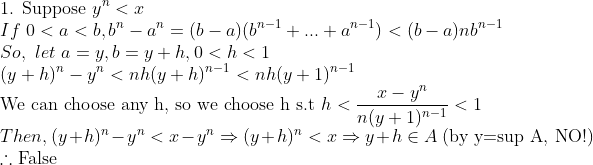

그러므로 y^n=x이다.
즉, 1번 경우에선, (y+h)^n을 y^n과 x 사이로 들어가도록 h를 뽑아내었고, 2번 경우에도, 마찬가지 방식으로 k를 뽑아내었다.
지금까지 실수에 대해서 알아보았는데, 다음 챕터에서는 복소수(Complex Number) 개념으로 확장해보자!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 2-3. 열린 집합과 닫힌 집합의 성질(Property of Open / Closed set) (0) | 2023.02.05 |
|---|---|
| (해석학) 2-2. 거리 개념과 집합 (Basic Set Theory - Concept of Open / Closed Set) (0) | 2023.02.03 |
| (해석학) 2-1. 가장 만만한게 집합이지....? (Basic Set Theory - Countable/Uncountable) (0) | 2023.02.03 |
| (해석학) 1-2. 차원 확장! 복소수와 유클리드 공간 (Complex Field, Euclidean Space) (0) | 2023.01.31 |
| (해석학) 해석학 개요 (0) | 2023.01.02 |