이번 챕터에서 드디어 열린집합과 닫힌집합에 대한 내용을 들어간다. 용어들이 많이 나오므로, 잘 정리하면서 가보자.
먼저, Metric Space(거리공간)에 대해서 알아보자.
(Metric(거리))

위 3가지 식(특히, 삼각부등식)을 만족하는 함수를 metric이라고 부르고, 이 metric이 존재하는 공간 X를 metric space라고 부른다.
보면 알겠지만, metric은 상대적인 것이지만(두 점), norm은 원점(절대적인 기준)이 요구가 되는 것 같다...
사실, 우리가 대부분 작업하는 공간 자체가 Euclidean Space이기 때문에, 그냥 d(x,y)보다 |x-y|로 쓰는 경우도 있다. 최대한 구분하려고 쓰려고 노력하겠지만, 해석학 카테고리에서 혼용해서 쓸 수도 있을 것 같아서 참고바란다.
자, 이 metric space에서 Open set과 Closed set이 정의가 된다.
먼저, 열린(닫힌) 구간의 확장판인, open(closed) ball에 대해서 살펴보자.
(Open(Closed) Ball)

단지, 구간의 확장판이라고 생각하면 된다. 아래에서 open set, closed set을 보고 오면 왜 이름이 open/closed로 붙었는지 바로 알 것이다.
또한, Euclidean Space에서는 cell이란 용어도 있는데,
(k-cell in R^k)

또, Convex set은 다음과 같이 정의한다.
(Convex set)
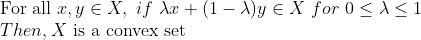
즉, X에서 두 점을 잡으면, 두 점을 이은 선분이 X 안에 있어야 한다는 것이다.
아래 그림에서 왼쪽은 convex, 오른쪽은 convex가 아니다(빨간 선)

이를 바탕으로 Open Set과 Closed Set을 정의해보자.
1-a. (Interior Point)
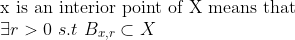
x에서 open ball을 잡을 때, X 안으로 들어갈 수 있으면 된다는 것이다. (X는 검은 색 원과 내부)
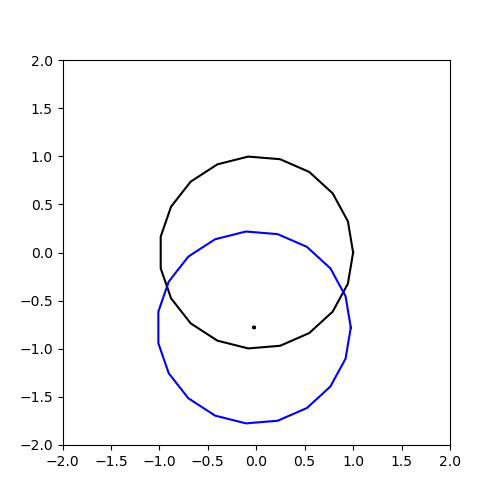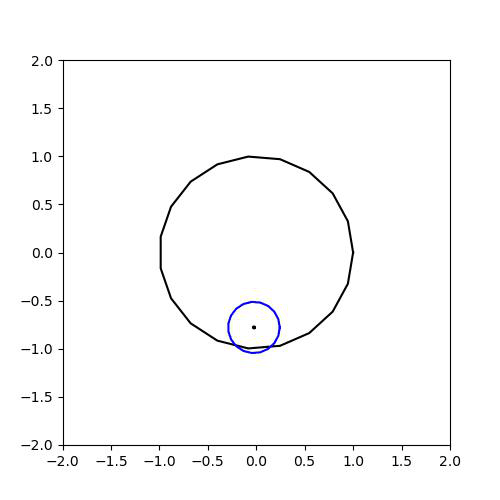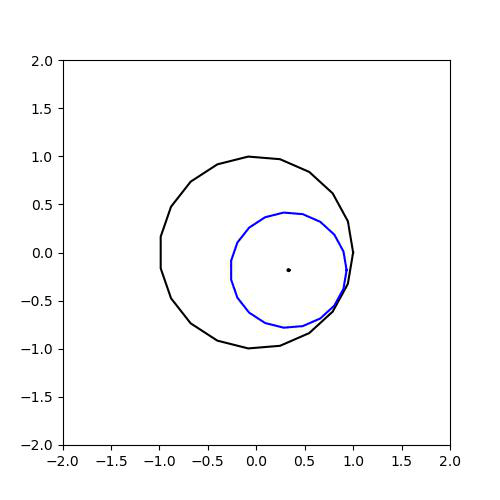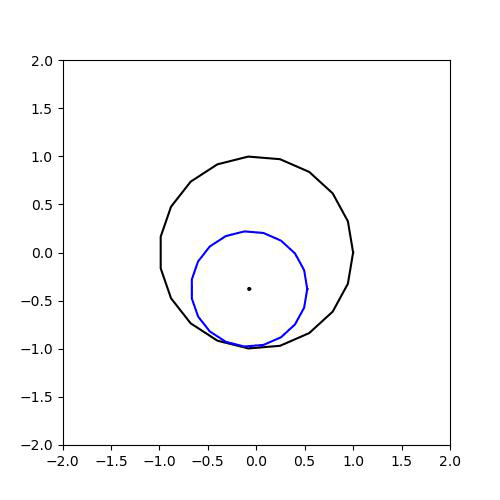
1-b. (Open Set(열린 집합))
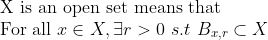
즉, X의 모든 점이 interior point이면 X는 열린 집합이 된다.
2-a. (Limit Point) <-> (Isolated Point)

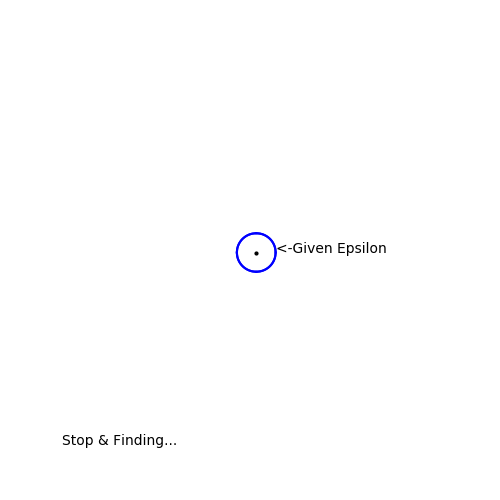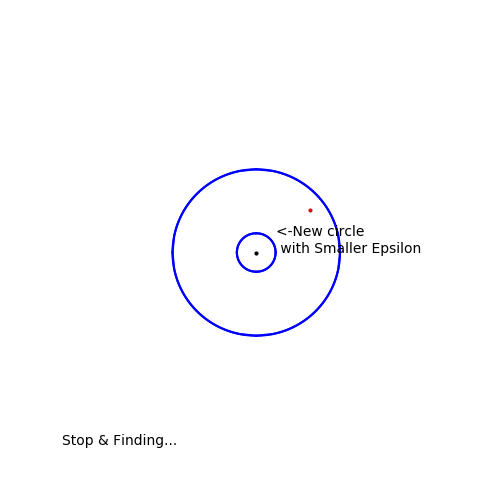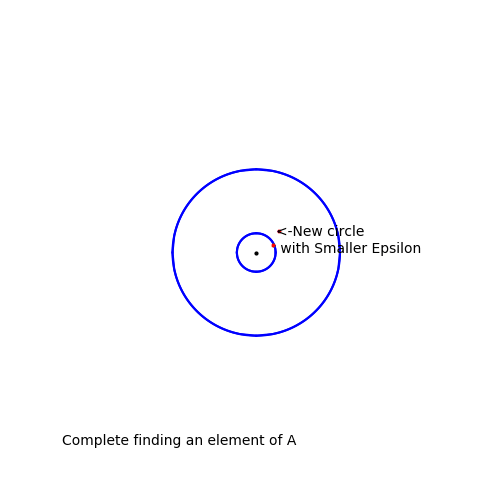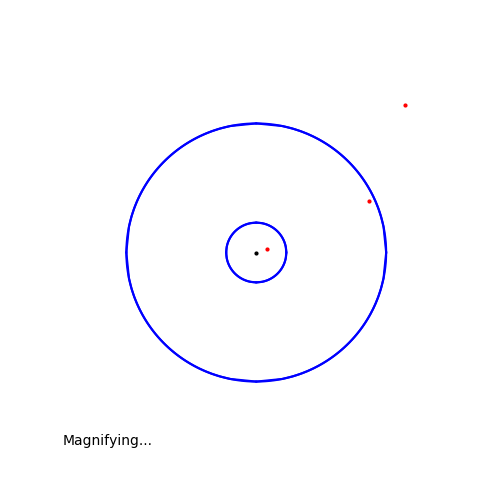
그러니까 아무리 작게 반지름 r을 잡아도, 자기 자신을 제외하고 X와 겹치는 원소가 있다는 말이다.
입실론-델타 논법과 결국엔 동일한 개념인데, 위의 그림에서 x를 검은 점, 반지름을 epsilon이라고 하면, 아무리 epsilon을 작게 해도 겹치는 점(빨간 점)이 있다는 것이다.
또한, Isolated Point는 X에 존재하면서, limit point가 아닌 점이다.
즉, Isolated Point에서는 open ball을 잡을 때, X와 겹치지 않도록 반지름을 잡을 수 있다.

interior point에서 본 그림이지만, 여기선 다르게 해석하자.
검은 원의 밖을 X라고 하고, 잡힌 원의 중심이 X에 속해있다고 생각하면 Isolated Point라는 이름이 당연하다고 느껴질 것이다. (X와 떨어져 있다...)
여기서 저 열린 집합과 닫힌 집합이 무슨 연관이 있겠다고 생각하면, 그 생각이 맞다. 용어 정리 후에 살펴보자.
2-b. (Closed Set(닫힌 집합))
X의 모든 limit point가 X의 점인 경우 Closed set이라고 한다.
Open set에선 X의 모든 점이 interior point이었는데, 여기선 반대라는 점을 주목해야 한다!
예를 들어서 설명해보자.
X={1} 이라고 하면, X의 limit point는 없다!
왜냐면, 어떤 점(1과 아주 가까울수도...) x=a라는 점을 잡으면, 반지름을 |1-a|보다 작게 잡으면 겹칠 수 없다!
또한, x=1의 경우 X와 겹칠 수 없으므로(자기자신은 포함 안한다) isolated point가 되고,
결국 그 어떤 점도 X의 limit point가 될 수 없다.
Closed set의 정의에 따라서, X는 Closed set이다! (즉, limit point가 없으니, 모든 limit point (공집합)가 X에 속하므로.)
(즉, Isolated Point는 Closed set이다)
그러니까, Closed set의 경우에는 Isolated Point의 경우가 있기 때문에
-> "모든 점이 limit point인 경우 Closed set이다" 의 정의는 틀렸다고 할 수 있다.
3. (Perfect set)
X의 모든 점이 limit point이고, 모든 limit point가 X의 점(Closed set)인 경우 Perfect set이라고 한다.
즉, Isolated Point가 없는 경우의 Closed Set을 말한다.
4. (Bounded set)
모든 점에 대해서 metric(실수)에 대해서 유계인 집합을 말한다. 즉,

이 말은, 결국 X가 open ball로 감싸진다는 것을 이야기한다.
5. (Dense set)
X is dense in Y 는, X의 모든 점이 Y의 limit point이거나 Y의 점임을 뜻한다.
예를 들어서, 유리수집합은 실수집합의 dense subset이다. -> 실수를 구성하는 파트에서 나온다.
일단, 용어에 대한 정리는 이 정도로 하고, 개념을 잡기 위해서 예시를 몇개 들어보자.
ex1) Open Ball은 Open set이다!
사실 위의 그림으로도 본 것이지만, 증명을 해보자.

여기서 절댓값 대신에 그냥 metric을 써도 똑같은 결과이다.
차이점을 느끼기 위해 Closed Ball이 Open set이 아닌 것을 확인해보자. Closed ball의 예시로 [-1,1]을 생각하자.
x=1에서 어떤 open ball (1-r,1+r)을 잡아도, 아무리 반지름을 작게 잡아도, 1보다 큰 경우가 생기므로, open set이 될 수 없다.
위의 open ball은 bounded set이다.
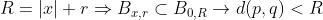
ex2)

(풀이)
먼저, A의 극점은 x=1이다.
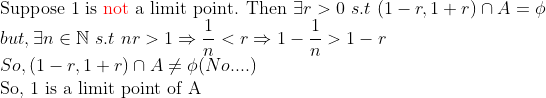
여기서 앞에서 본 아르키메데스 성질을 사용했다!
x=1이 아닌 경우 -> x가 0과 1 밖에 있으면 trivial...(생략), x가 0과 1 사이에 있다면
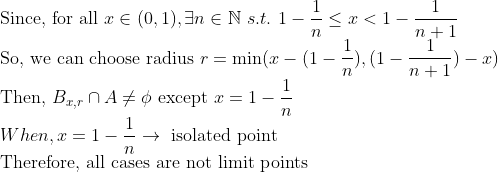
그러므로, A는 Closed set이다.
ex3) 공집합은 open set이기도 하고, closed set이기도 하다!
-> 굳이 따지자면 모든 점(nothing)에 대해서 성립하므로, 조건을 다 만족시킨다.
-> 후에 나오겠지만, 공집합의 여집합인 좌표평면 또한, open set이기도 하고, closed set이기도 하다.
ex4) Open ball은 Closed set이 아니다!
ball의 경계(=r)가 limit point가 되지만, open ball에 포함되어 있지 않아, closed set이 아니다.
ex5) A=[0,1)은 open set도, closed set도 아니다!
후에 나올 open set과 closed set의 관계 때문에 모든 set이 open / closed로 구분이 되는 것 같이 보이나, 이런 구간은 open도, closed도 아니다
여기까지, open set과 closed set의 개념에 대해서 알아보았다.
생소한 용어들이 많이 나와서 꽤나 어려울 수도 있겠지만, 이 내용들이 아주 중요하므로, 확실히 알고 넘어가자.
다음 챕터에선 open set과 closed set의 성질들에 대해서 살펴본다.
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 3-1. 전혀 컴팩트하지 않은 compact set.... (What is Compact set?) (0) | 2023.02.05 |
|---|---|
| (해석학) 2-3. 열린 집합과 닫힌 집합의 성질(Property of Open / Closed set) (0) | 2023.02.05 |
| (해석학) 2-1. 가장 만만한게 집합이지....? (Basic Set Theory - Countable/Uncountable) (0) | 2023.02.03 |
| (해석학) 1-2. 차원 확장! 복소수와 유클리드 공간 (Complex Field, Euclidean Space) (0) | 2023.01.31 |
| (해석학) 1-1. 도대체 뭐가 문제라 증명을 못했을까? (What is Real Number?) (2) | 2023.01.31 |



