지난 챕터에선 실수가 과연 무엇인지 약간 맛을 보았고, 실수의 완비성에 관해서 이야기하였다.
이번엔 이를 확장해서 복소수와 더 일반화된 공간에 대해서 살펴보자.
다만, 유리수체에서 실수체를 뽑아내는 것처럼은 실수에서 복소수를 뽑아내는게 불가능하다는 것은 실수의 완비성에 의해서 당연하다. 그러면, 어떻게 복소수체를 구성할까? -> 차원 UP
(Complex Number)(복소수)
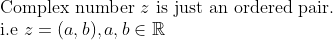
미적분학 카테고리에서도 살짝 언급을 하긴 했지만, 복소수는 단지 실수 2개의 순서쌍으로 정의하면 된다.
그리고 i=(0,1)이라고 정의하면, 우리가 아는 것처럼 복소수를 z=a+bi으로 표현할 수 있다.
그리고, 복소수의 덧셈과 곱셈을 다음과 같이 정의하자.
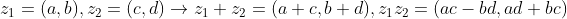
그러면, 복소수집합은 체(Field)가 된다.(증명은 생략)
또한, 우리가 이미 알듯이 복소수에서는 Conjugate(켤레수)를 정의한다.
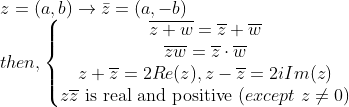
특히, 3번째 식은 식을 정리할 때, 아주 많이 쓰인다!
또, 4번째 식은 복소수에서 절댓값(absolute value)을 정의할 때 쓰게 된다.
그 전에 복소수 공간에서 내적을 정의하자.
(Inner Product in Complex Field)
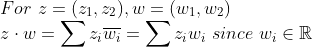
(Note)
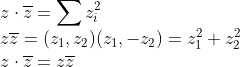
(Absolute Value in Complex Field)

위에서 zz_bar가 실수임을 알 수 있고, 앞 챕터에서 0보다 큰 실수의 루트값이 0보다 큰 실수이고 unique함을 보였으므로, 모든 복소수 z의 absolute value는 양수이고 unique함을 알 수 있다.
(성질)

특히 5번 삼각부등식(Triangle Inequality)은 아주 많이 등장할 예정이므로 꼭 기억하자.
또한, 학교다닐 때 꽤나 보았을 Cauchy-Schwarz Inequality(코시-슈바르츠 부등식)도 등장한다.
(Cauchy-Schwarz Inequality in Complex Number)
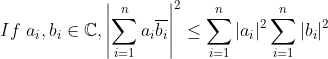
(a와 b가 모두 실수라면)
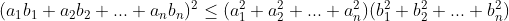
(증명)
Cauchy-Schwarz Inequality는 아주 많이 사용하므로 꼭 알아야 놓아야 한다.
복소수를 정의하기 위해 차원을 올렸는데, 그렇다면, 더 차원을 높일 수도 있지 않을까???
(Euclidean Space)(유클리드 공간)

이렇게 이루어진 공간 R^n을 Euclidean Space라고 한다.
이 때, 벡터의 덧셈과 상수(스칼라)배를 각각 덧셈과 곱셈으로 생각하면 연산에 대해 닫혀있고, 체(Field)의 조건(교환법칙, 분배법칙, 항등원과 역원 등...)을 당연히 만족한다. 그러므로, R^n 은 벡터공간(Vector Space)이 된다.
또한, inner product(내적)과 norm을 다음과 같이 정의할 수 있다.

그러므로 Euclidean Space는 내적 공간(내적이 정의되는 공간), norm space(norm이 정의되는 공간)를 이룬다.
(여기서는 벡터 공간과 norm의 의미 등에 대해서는 선형대수에서 더 살펴보도록 하고, 잘 모르겠다면, 그냥 그렇다... 정도로 생각하자.)
유클리드 공간에서도 코시-슈바르츠 부등식이 성립한다.
(Cauchy-Schwarz Inequality)

(Note) 사실, Cauchy-Schwarz Inequality는 내적 공간에서의 일반적인 성질이다.
(증명)

Cauchy-Schwarz Inequality를 쓰면 된다! (복소수에서 conjugate 처리하는 것이 더 일반적이라고 생각하면 된다!)
또한, 내적이 정의되었으므로, Norm도 정의 가능하다. -> Norm space이므로, norm의 일반적인 성질은 다 만족한다.
즉, (Norm 성질)

사실 성질이라고 이야기 했지만, 애초에 위의 4가지 성질을 다 만족하도록 잡은 함수를 norm이라고 정의한다.
그러므로 정리하면!
복소수체 -> 내적을 정의하면 norm도 복소수의 절댓값으로 정의
유클리드 공간 -> 내적을 정의할 수 있으므로 norm 정의
내적공간에서는 코시-슈바르츠 공식이 성립
또한, norm 공간( -> 거리(metric)가 정의됨) -> 삼각부등식 성립
이번 챕터에서는 복소수의 정의와 유클리드 공간에 대해서 살펴보았는데, 뭔가 어렵게 써놓기는 했지만, 별거 아니다...
다만, norm과 내적에 대해서 나중에는 기존에 알던 것과 다른 관점으로 보아야 하기 때문에 약간 거리감이 있도록 다시 한번 개념을 체크하는 것도 좋을 것 같다.
다음 챕터에서는 그렇게 찾아해매던 topology와 집합에 관한 이야기를 할 것이다. 여기부터는 기존에 하던 것과는 꽤나 달라서 생소할 수 있어 어려울 수 있으므로 설명을 잘 따라오길 바란다!
'Mathematics > 해석학' 카테고리의 다른 글
| (해석학) 2-3. 열린 집합과 닫힌 집합의 성질(Property of Open / Closed set) (0) | 2023.02.05 |
|---|---|
| (해석학) 2-2. 거리 개념과 집합 (Basic Set Theory - Concept of Open / Closed Set) (0) | 2023.02.03 |
| (해석학) 2-1. 가장 만만한게 집합이지....? (Basic Set Theory - Countable/Uncountable) (0) | 2023.02.03 |
| (해석학) 1-1. 도대체 뭐가 문제라 증명을 못했을까? (What is Real Number?) (2) | 2023.01.31 |
| (해석학) 해석학 개요 (0) | 2023.01.02 |




