지난 챕터에서는 Open set과 Closed set의 개념에 대해서 살펴보았다면, 이번에는 성질들을 몇 개 알아보자.
1. (Limit Point)에 관한 성질
-> 만일, x=p가 limit point of A이면, 중심을 p로 가지는 모든 open ball은 A의 원소를 무한개 가지고 있다!
(If x=p is a limit pt of A, then, all B(p,r) has infinitely many elements of A)
-> 즉, 반지름 r을 어떻게 잡던지, A의 원소를 무한개 가지고 있다.
-> 즉, 유한집합은 limit point를 가질 수 없다.
(증명) -> 대우로 증명
만일, 어떤 open ball이 A의 원소를 유한개 가지고 있다고 하자.
그러면, 그 중에서 p와 가장 가까운 A의 원소를 q라고 하자. 이때, 둘 사이의 거리를 d(p,q)라고 하자.
만약에 반지름 r을 d(p,q)보다 작게 잡으면, 그 open ball은 A의 원소를 가지지 않는다. -> x=p가 limit point가 아니다! (모순)
그러므로, 모든 open ball은 A의 원소를 무한개 가지고 있어야 한다.
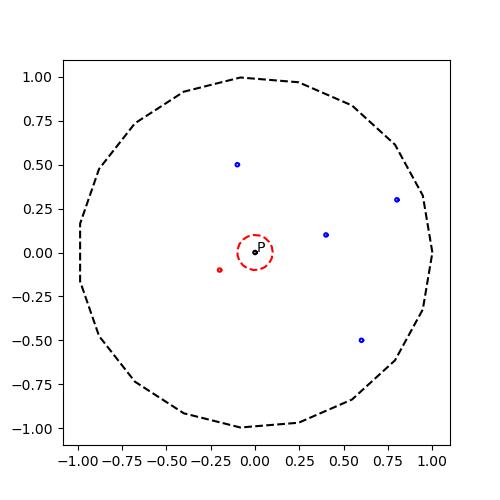
2. (Open Set과 Closed Set의 관계)

(증명)
사실, open set 정의의 대우가 closed set의 정의가 된다.

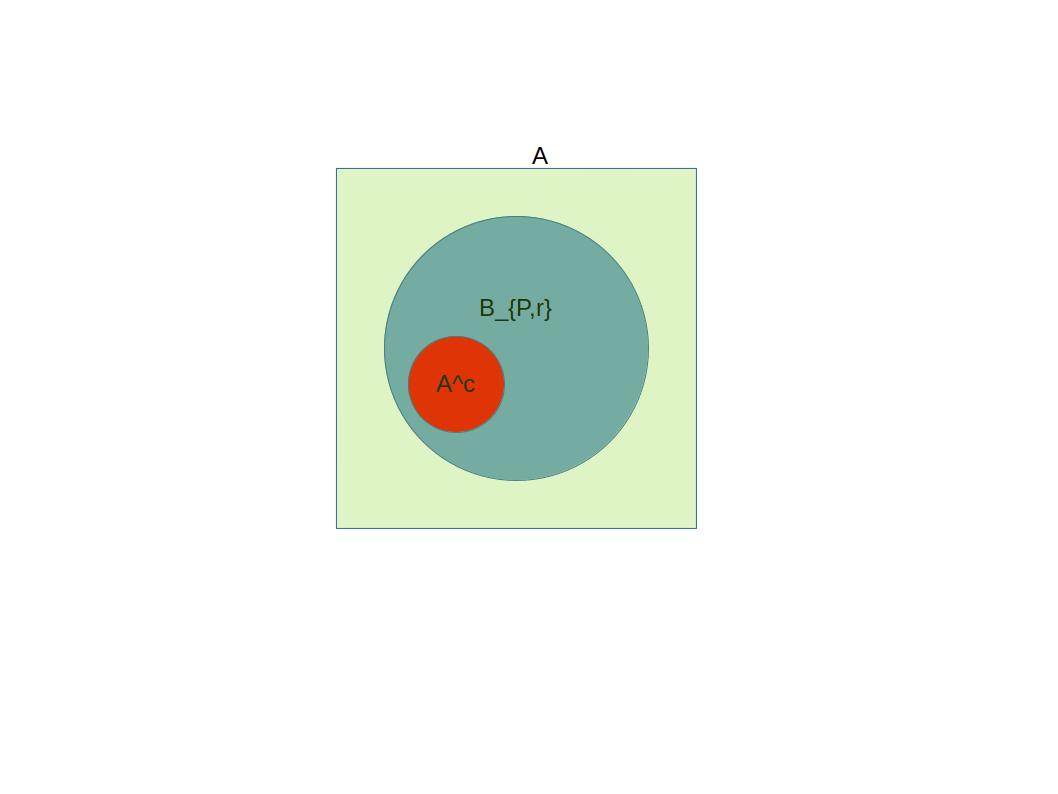
반대의 경우는
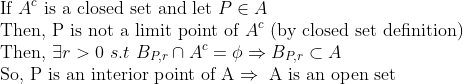

특히 증명의 세번째 줄은 아주 잘 써먹으니까 꼭 알아두자.
유용하게 잘 써먹을 곳이 많으니 꼭 기억해두자. 그리고, 앞 챕터에서도 보았듯이, 모든 set이 open과 closed로 나뉘는 것은 아니라는 것을 참고바란다.
(NOTE) union과 intersect의 관계
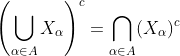
증명할때, 벤 다이어그램을 쓰면 안되긴 하지만, 워낙에 직관적이라 따로 설명을 하지는 않겠다.
이 때, 저 X_a가 유한개던지, 무한개(countable/uncountable)던지 다 성립을 한다.
일단, union, intersect 관계를 이용한, open set과 closed set의 성질들을 더 보자.
3.(Union / Intersect of Open, Closed Sets)

(증명)
1.

2.

3. 위의 Union/Intersect 관계와 open/closed set의 여집합 관계를 1번에 쓰면 된다.
4. 3번과 마찬가지로 하면 된다.
5번의 경우에는 주의해서 생각하자! open인지, closed인지, 혹은 둘 다 아닌지 때에 따라 다를 수 있다.
Closed set에 대해서 조금 더 들어가서, closure(폐포)에 관해서 알아보자.
(Closure(폐포))

즉, A와 그 극점의 집합의 합집합이다. 여기서 나오는 A'도 계속 쓰는 notation이니 체크하자.
Closure와 관련된 몇가지 성질을 체크하면
(Closure 성질)

(증명)
1. (여기서 A'는 당연히 closed set이다)

2.
1에 의해서 trivial한 결과이다!
3.
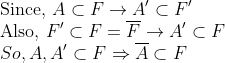
A의 극점에선, 항상 A의 원소를 가지는 open ball을 가지는데, A의 원소가 F의 원소이니 결국 F의 극점이라고도 할 수 있다. (첫번째 줄) 그리고, 두번째 줄은 2번 결과를 이용하였다.
1번 성질을 꼭 기억하고,
3번 성질의 의미는 closed set F의 부분집합 A에 대해서, A의 Closure 정도까지는 부분집합에 포함된다는 것이다.
(Corollary)
만일, 실수축에서 생각한다면

즉, supremum과 infimum는 closure에 존재하므로, 닫힌 구간을 잡을 때는 그 구간 안에 supremum과 infimum이 존재하게 된다.
(증명)
마지막으로 open set과 closed set의 상대적인 개념을 알아보자.
다음과 같은 set을 생각해보자.
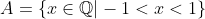
만일, 우리가 주목하는 metric space가 유리수 집합 Q였다면, A는 당연히 open set일 것이다.
그러나, 실수(R) 위에서는 유리수 중간중간에 실수가 들어가 있기 때문에, A의 그 어떤 원소에서도, open ball을 잡으면, 유리수가 아닌 실수가 중간에 끼어들어가므로, open ball이 A 안에 들어갈 수 없다. -> 즉, open set이 아니다!
이렇게, open / closed는 metric space에 상대적인 개념이다.
그러므로 Open / Closed의 상대적 개념을 다음과 같이 정의한다.
(Open/Closed relative to Y)
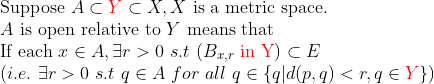
Closed set인 경우에도 동일하게 적용하면 된다.
후에 연속함수에서 써먹을 성질 하나를 소개하고 마친다.
(Open Relative to... -> 성질)

E는 Y에 대해 open이고, G는 X에 대해서 open이라는 점을 확인하자!
(증명)
1. -> X에 대한 open ball을 따로 잡아보자!
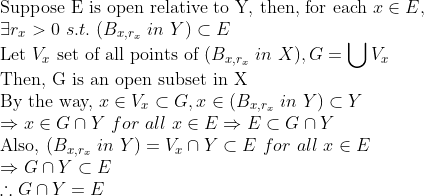
2. <-

여기까지, open set과 closed set의 성질에 대해서 알아보았다.
여기서 나온 내용들은 사실 다 많이 쓰는 성질들이라서 뭐 하나 빼기도 어려웠고, 사실 증명 방법도 여기서 많이 연습하고 가는 것이 좋을 것이다.... (사실 쓴 건 open과 closed 사이의 관계를 증명할 때 집합간의 포함관계 정도가 될텐데, 많이 써먹는 만큼 꼭 알고 가자)
그러나 아직까지는 이게 도대체 왜 최대최소정리를 증명하는데에 쓰이는지 아마 감도 안 잡힐 것 같다...
그러나, 다음 시간부터 나올 COMPACT SET에 관해서 알고 난 후, 정리한 것을 생각해보면, 이래서 쓰는구나...라는 생각이 들 것이다.
참고로, compact set은 해석학 초반의 가장 큰 장벽이기도 하지만, 거의 해석학의 중심적인 내용이 되기 때문에, 어려워도 꼭 알고 가야한다!!




