지금까지 1차, 2차 미분방정식에 대해서 살펴보았다.
더 고차의 미분방정식도 접근방식이 동일하다!
(Definition of N-th order Linear Ordinary Differential Equation)
다음 식을 N차 선형 ODE로 정의할 수 있다.
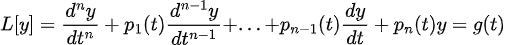
이 때, 초깃값은 다음과 같이 주어진다.

=> 이를 만족하는 식 y(t)를 구하는 것이 우리의 목적이다!
또한, n차 선형 ODE는 다음과 같이 구분할 수 있다.
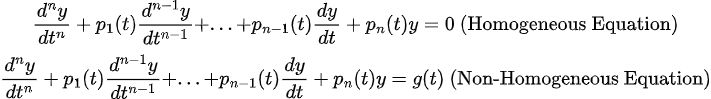
=> 그러면, 2차 선 ODE에서 본 것 같이, 해는 다음과 같이 n개의 Basis(y1, y2, ...., yn)으로 구성된다.
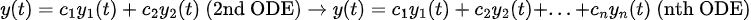
=> 2차 ODE와 마찬가지로 Wronskian을 다음과 같이 정의할 수 있다.
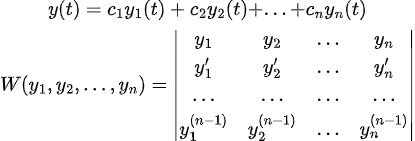
=> 2차 ODE와 모든 성질이 동일하기 때문에, 자세한 내용은 패스하도록 한다...
(Example 1)
(Abel's Theorem in nth-ODE)
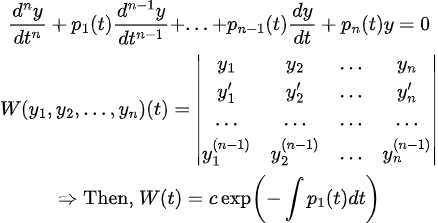
(Solution)
먼저 Wronskian의 미분값을 구해보자. 이때 Determinant 성질을 잘 이용하면 쉽게 구해볼 수 있다.
(Lemma1)
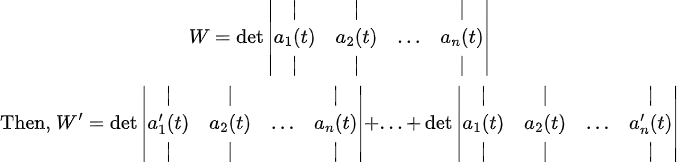
(증명)
(1)
먼저, 2 by 2 부터 증명해보자.
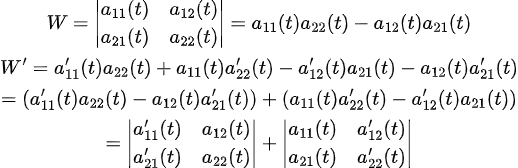
2 by 2까지는 쉬운데, 고차원으로 올라가면 약간 복잡해진다... (혹은, 필자가 몰라서...)
(2)
Determinant의 정의를 생각해본다면...
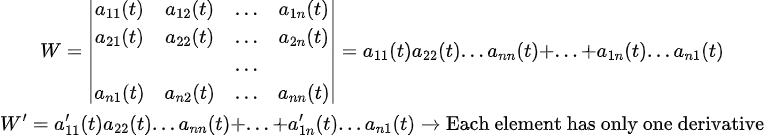
일단 부호는 제쳐놓고, Determinant 식을 모두 풀어쓰면, 각 행과 열에서 하나씩 골라온 것들을 곱해서 모두 더한 것과 동일하다.
1. W의 각 성분 : 행렬의 각 행과 열에서 행과 열이 겹치지 않도록 1개씩 골라온 것들을 모두 곱한 것
ex)
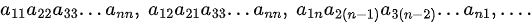
2. W : 이 성분들의 총 합

그러면 이 식을 미분해보자.
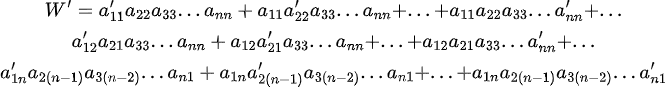
아까 본 W의 각 성분에 1개씩 미분항이 들어갈 것이다. (물론, 각 성분에서 n개 중 어떤 걸 미분하냐에 따라서 경우의 수가 많아질 것이다.)
즉, W'의 전체 성분은 다음과 같이 뽑아낼 수 있다.
1. W처럼 각 행과 열에서 성분을 뽑아내는데, n-1개를 뽑아 온다.
2. 나머지 1개의 행/열 성분은 미분한 값으로 뽑아온다.
3. W'는 이를 다 더한 값이다.
(3)
Cofactor에 대한 다음 정리를 이용하면....
https://0418cshyun.tistory.com/168 참고!!!

이 때, a_11~a_n1의 미분항은 Cofactor들의 미분항에 들어가 있지 않은 것을 알 수 있다.
즉, (2)와 결부해 생각해보면
위의 Determinant는 2행~n행에서 n-1개의 함수를 가지고 오고, 1행의 것만 미분항을 넣은 Term이라고 할 수 있다.
게다가, 동일한 방식으로 다음 식을 얻을 수 있다.
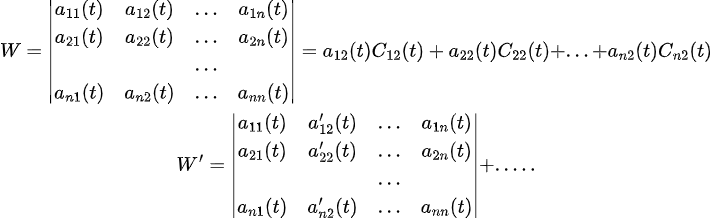
이 때의 Cofactor의 미분항에서도 a_12~a_n2의 미분항은 존재하지 않는다.
이 때에도 위의 Determinant는 1행,3행~n행에서 n-1개의 함수를 가지고 오고, 2행의 것만 미분항을 넣은 Term이라고 할 수 있다.
즉, 다음 식은 (2)에서 요구한 사항을 모두 만족한다.

그러므로, W'는 위 식과 동일하다.
게다가 부호의 경우도 각 sub-determinant에서 정해지기 때문에, 신경 쓸 필요가 없다.
(Lemma 2)

(증명)
Determinant는 Row/Column에 대칭이므로, 위의 Lemma 1을 이용한다면 간단히 구할 수 있다.

그러면, 이 성질들을 이용해서 Abel's Theorem을 증명해보자.
Determinant 계산에 익숙하다면, 간단할 것이다!

Q.E.D
사실, lemma1이 증명하기 까다로워서 그렇지, Determinant에 익숙하다면, 나머지 내용은 간단하다.
(Example 2)
어려운 문제를 증명했으니, 쉬운 예제를 가보자!
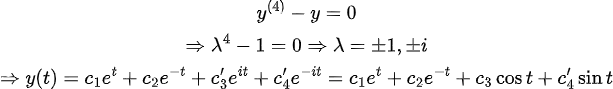
아주 심플하다!!!
(Example 3)
(중근이 많이 나오는 경우)
https://0418cshyun.tistory.com/206 참고!!!

특성방정식을 구해보면...
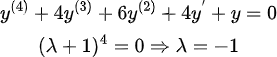
중근이 총 4개씩이나 나온다....
기존에 구했던 IDEA를 이용해보자!
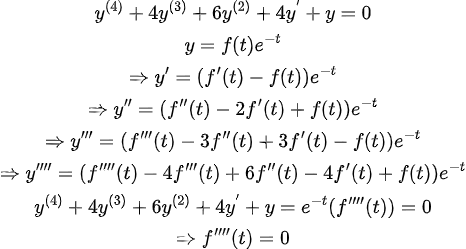
즉, f''''(t)=0이 되는 식 3개를 더 구하면 총 4개의 basis를 채울 수 있다.
어렵게 생각할 필요 없이, f(t)는 다음과 같다.
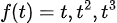
그러므로 위의 방정식의 해는 다음과 같다.
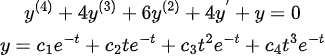
=> 지금까지 보면 알겠지만, 중근이 나오는 경우 나오는 만큼 t를 곱해주면 된다!!
(Example 4)
(복소수 중근이 나오는 경우)
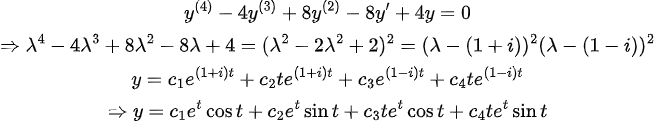
=> 복소수 중근이 나와도 똑같이 t를 곱해주면 된다!! (위와 같이 증명해주면 된다!!)
이번에도 2차 ODE 처럼 Variation of Parameter를 이용해서 일반해를 구해보자!!
(Variation of Parameter)
다음 식의 해를 구해보자!
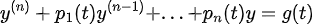
그러면, 일반해의 형태는 이미 알다시피
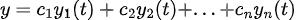
그러면, Variation of parameter를 이용해보자!
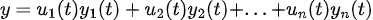
자, 그러면 이 식을 다시 원래 식에 집어넣기 위해 미분해보자.
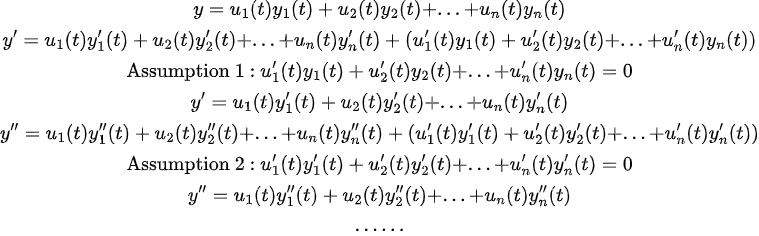
이 때, 2차 ODE 때 처럼 u'가 나오지 않게하기 위해 가정을 집어 넣어가면서 미분한다
자, 그러면 결국 다음과 같다.

이 때, i=n-1까지이다!!
i=n인 경우에는...
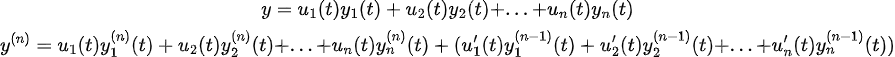
우리가 구한 미분값으로 원래 식에 집어넣으면 다음과 같다.
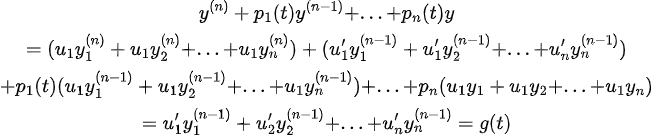
이를 위의 가정과 행렬로 표현하면

미분방정식의 해가 존재하는 경우 아까 본 Wronskian의 역행렬이 0이 아니므로, 각 u를 구할 수 있고, 이를 적분하여 일반해를 구하면 된다!

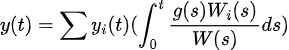
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 부록 2. Non-Constant Coefficients & Nonlinear ODE (0) | 2025.05.18 |
|---|---|
| (미분방정식) 부록 1. Wronskian (Advanced) (0) | 2025.05.18 |
| (미분방정식) 8-2. Nonhomogeneous ODE - Variation of Parameters (0) | 2025.05.18 |
| (미분방정식) 8-1. Nonhomogeneous ODE - Method of Undetermined Coefficients(미정계수법) (0) | 2025.05.17 |
| (미분방정식) 7-3. 2nd-Order ODE with Constant Coefficients (3) (1) | 2024.01.06 |



