이번에는 Wronskian에 대해서 조금 더 자세히 알아보자.
1. 선형결합과 Wronskian
여기서 우리가 알아볼 것은 2차 ODE의 해에서 나오는 2개의 함수 y_1, y_2가 서로 linearly independent하다는 것이다.
먼저, 미분가능한 함수 f,g가 있다고 하자. 그러면 다음이 성립한다.
<Wronskian & Linear Independence>
1. f,g가 linearly Dependent이면, 모든 t에 대해서 W(f,g)(t)=0 이다.
2. 어떤 t에서 W(f,g)(t) ~=0 이면, f,g는 linearly independent이다.
(증명)
1번을 증명하면 2번도 바로 증명되므로, 1번만 증명해보자.
사실, 이건 선형대수학 내용만 알면 바로 증명되는 내용이다.

Q.E.D
위의 2번 내용을 다시 ODE와 엮어보자.

6-2, 6-3 에서 2차 ODE의 Initial Value Problem의 해를 구할 수 있다면, Wronskian은 초깃값에서 0보다 크므로, 결국 Homogeneous Solution의 y1, y2는 서로 선형 독립이다!
2. Abel's Theorem
Wronskian과 관련된 정리 중 하나를 소개한다.
IVP에서 W>0이어야 한다는 것이 초깃값 한 점뿐 아니라, 모든 점에서 W>0을 만족해야 한다는 정리이다.
<Abel's Theorem>
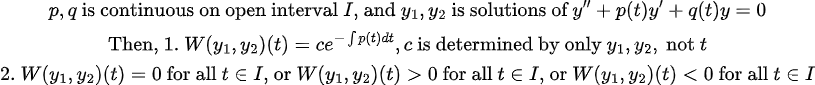
즉,
1. Wronskian 식은 p(t)에 대한 식과 y_1,y_2로 정해지는 c로 정리할 수 있다.
2. Wronskian은 I에서 0으로 상수함수 이거나, 0보다 크거나, 0보다 작다는 것이다. (0을 넘나들 수 없는 함수...)
(증명)

이 때 당연히 c는 적분상수로, t에 의해서 결정되는 것이 아니라, W에 의해 결정되므로, y_1,y_2에 의해 결정된다고 할 수 있다.
게다가, exp함수는 지수로 뭐가 들어가든(허수만 아니면) 0을 넘나들수 없으므로, W(t)는 0이거나, 0보다 크거나, 0보다 작다고 할 수 있다. (c에 따라서 W(t)의 부호가 결정)
다시, 2차 ODE로 오면, 초깃값 문제에서 해가 존재한다면 W(t0) > 0이어야 하므로 결국 해가 존재하는 범위 내에서 모든 t에 대해 W(t) > 0이라는 것을 알 수 있다!!
(정리)
1,2 내용을 정리하면 결국 다음 내용은 동치이다.
다음 ODE에서...
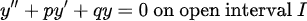
1. y1, y2가 I에서 Fundamental Set을 만족한다.
2. y1, y2가 I에서 Linearly Independent
3. W(y1,y2)(t0) > 0 (t0은 I의 한 점)
4. W(y1,y2)(t) >0 (t는 I 내의 임의의 점)
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 9. Higher-Order ODE (0) | 2025.05.25 |
|---|---|
| (미분방정식) 부록 2. Non-Constant Coefficients & Nonlinear ODE (0) | 2025.05.18 |
| (미분방정식) 8-2. Nonhomogeneous ODE - Variation of Parameters (0) | 2025.05.18 |
| (미분방정식) 8-1. Nonhomogeneous ODE - Method of Undetermined Coefficients(미정계수법) (0) | 2025.05.17 |
| (미분방정식) 7-3. 2nd-Order ODE with Constant Coefficients (3) (1) | 2024.01.06 |



