우리는 대부분 상수항을 가진 ODE를 보아왔는데, 이번엔 간략하게 상수항이 아니거나 비선형 ODE를 어떻게 푸는지 살펴보자.
먼저, 이미 배웠던 내용들을 정리해보자.
<적용할 수 있는 방법(현재까지)>
(1차 ODE)
- Nonlinear
1. 변수분리법
- Linear
1. 변수분리법
2. Integrating Factor (Variation of Parameters), (일반적인 해)
(2차 ODE)
- Nonlinear
1. 변수분리법
2. ???
- Linear
1. 특성방정식 해, 미정계수법 (상수항)
2. Variation of Parameters (일반적인 해)
(Example 1) <1차 ODE, 비선형>
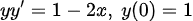
(풀이)
변수분리법 쓰면 바로 풀 수 있다.
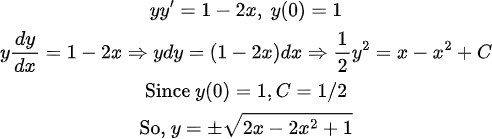
(Example 2) <1차 ODE, 비선형>
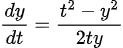
(풀이)
약간의 트릭을 사용하여 변수분리법을 쓰게 만들 수 있다.
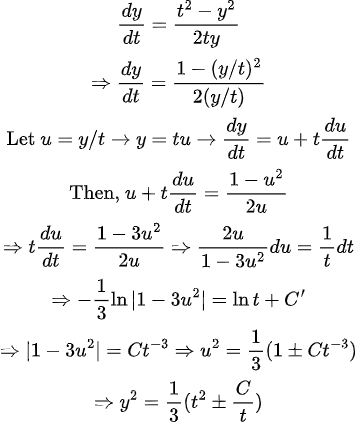
(Example 3) <Bernoulli's Equation>
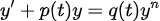
n=0인 경우를 제외하자. (n=0이면 Integrating Factor)
다음과 같이 치환하면, 비선형 ODE가 선형으로 변환된다.
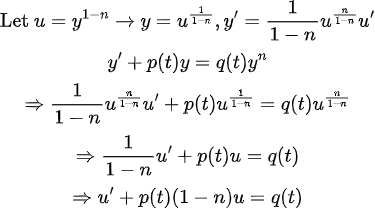
그러면, 다음 문제를 풀어보자.
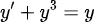
(풀이)
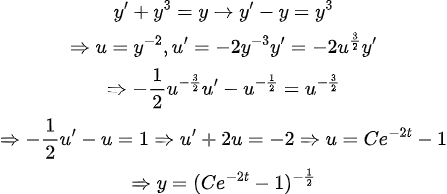
(Example 4) <2nd ODE, 비선형>
어떤 형태의 2nd ODE는 1차 ODE로 바꿔줄 수 있다.
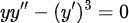
(풀이)
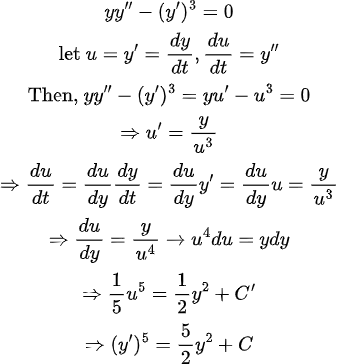
일단, 1차 Nonlinear ODE로 바꿔주기는 했는데, 저 식을 풀기가 복잡해서.... 일단 넘기도록 하자
(Example 5) <2nd ODE, Nonhomogeneous>
Chain Rule을 잘 이용하면, 복잡한 경우의 ODE도 풀 수 있다.
물론, 공식을 이용해서 풀어도 상관은 없으나, 그 경우에는 적분처리가 어려울 수 있다.
(풀이)
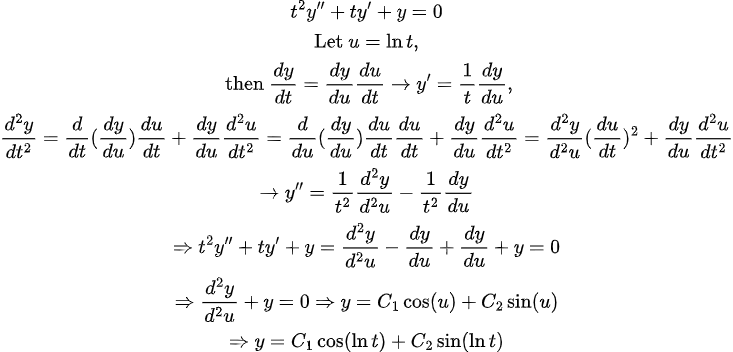
풀이 방식을 보면 알겠듯이, 대부분 변수치환을 통해 바꿔주는 방식을 택하는데, 어떤 변수를 취해야 할지 감이 오기가 쉽지 않은 경우도 많다. 또한, 이런 방식으로도 풀리지 않는 것들도 많기 때문에 Nonlinear ODE는 다 제각각의 방식을 사용해서 풀어야 한다.
하지만, 대부분의 경우 모델을 만들 때, 억지로라도 선형 ODE를 만들려고 노력하기 때문에 실제 Nonlinear ODE를 보는 경우는 흔치 않고, 일부 많이 사용하는 Nonlinear ODE의 경우(르장드르 식 등등...)에는, 접근하는 방식이 대부분 알려져 있다.
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 9. Higher-Order ODE (0) | 2025.05.25 |
|---|---|
| (미분방정식) 부록 1. Wronskian (Advanced) (0) | 2025.05.18 |
| (미분방정식) 8-2. Nonhomogeneous ODE - Variation of Parameters (0) | 2025.05.18 |
| (미분방정식) 8-1. Nonhomogeneous ODE - Method of Undetermined Coefficients(미정계수법) (0) | 2025.05.17 |
| (미분방정식) 7-3. 2nd-Order ODE with Constant Coefficients (3) (1) | 2024.01.06 |



