이번에는 지난시간에 이어서 Nonhomogeneous ODE를 푸는 두번째 방식에 대해 알아보자.
(Homogeneous Form)

(Non-Homogeneous Form)
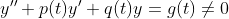
(Method of Undetermined Coefficient ) VS (Variation of Parameters)
2. Variation of Parameters(한국말로 뭐라고 하는지 잘 모르겠네요....)
미정계수법은 g(t)를 모르면 아예 접근이 불가능한 방식이었다. 이번에는 다른 방식으로 Nonhomogeneous ODE를 접근해보자.
우리가 Homogeneous ODE에서 선형 및 중첩 원리 이야기를 하면서 Solution을 다음과 같이 잡았었다

그렇다면, Nonhomogeneous ODE도 해의 형태는 크게 차이나지는 않을테니, 저 상수 2개를 "함수"로 잡으면 해가 되지 않을까?? 즉,

그러면, 이를 가정하고 Nonhomogeneous ODE 문제를 풀어보자...

흠.... 더 이상 정리할 수가 없어보인다.
여기서 저 식을 정리하기 위해서 u와 v에 대한 한가지 가정을 더 추가해보자. (일단 저렇게 가정해도 되냐고 묻지는 말자)

그러면 앞의 식은 다음과 같이 바뀔 것이다.

그러면, u',v'에 대해서 다음 식을 얻을 수 있다.

그러면, 역행렬을 이용해서 u',v'를 얻을 수 있다!

(여기서 W는 Wronskian이고, Initial Value Problem에서 항상 0보다 크다는 것을 보였으므로(6-2 참고), 역행렬이 항상 존재한다.
즉, 저 역행렬이 없다는 말은 애초에 Homogeneous Solution 조차도 없다는 얘기가 된다.)
그러므로, Nonhomogeneous ODE의 Solution은 다음과 같다.

여기서 풀이(가정이나, 왜 저렇게 푸는가)에 대해서 궁금증을 갖는 것이 당연할 수 있다. 여기에 대해 2가지 이해방식에 대해서 말할 수 있을 것 같다.
1. 그냥 이 방식을 받아들이자.... 어떻게든 ODE를 풀어내는 방식이라고 생각하면 된다. 온갖 가정을 다 넣어 어떻게든 해를 구했으니, 위에서 구한 해는 (틀림없이...) ODE의 해이다. 그리고, 저 ODE의 해는 유일하기 때문에(해의 유일성은 나중에 언급), 그냥 위의 식을 사용하면 된다.
2. Homogeneous Form에서 Nonhomogeneous Form으로 바뀐 것은 =0 -> =g(t)로 "1개"의 조건이 바뀌었다.
그런데, 우리가 2개의 상수(함수)를 2개의 임의의 함수로 바꿨으므로, 2개의 구속조건을 풀어준 것이나 다름없다.
그러므로, 1개의 자유도가 남으므로, 1개의 구속조건을 우리가 임의로 줄 수 있다. 이 구속조건을 식정리를 위해 u'y_1+v'y_2=0으로 준 것으로 생각하면 된다.
이 Variation of Parameters 방식은 미정계수법과 다르게 g(t)의 형태를 몰라도 그냥 사용할 수 있다. 그냥 2차 ODE를 푸는 공식처럼 생각해도 무방할 것 같다.
또한, 1차 ODE와 비교해본다면(2-2 참고), 결국 Integrating Factor에서 했던 얘기와 동일한 것을 알 수 있다.
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 부록 2. Non-Constant Coefficients & Nonlinear ODE (0) | 2025.05.18 |
|---|---|
| (미분방정식) 부록 1. Wronskian (Advanced) (0) | 2025.05.18 |
| (미분방정식) 8-1. Nonhomogeneous ODE - Method of Undetermined Coefficients(미정계수법) (0) | 2025.05.17 |
| (미분방정식) 7-3. 2nd-Order ODE with Constant Coefficients (3) (1) | 2024.01.06 |
| (미분방정식) 7-2. 2nd-order ODE with Constant coefficients (2) (1) | 2024.01.06 |



