이번에는 Determinant를 이용해서 역행렬을 구하는 방법을 알아보자.
역행렬을 구하는 공식이라고 하면, 크게 2가지로 볼 수 있다.
1. 가우스-조던 소거법 => 계산이 심플함
2. Determinant를 이용해서 역행렬을 구하는 것 => 수식으로 되어 있음, Recursive
가우스-조던 소거법은 앞 챕터에서 보았으므로, Determinant를 이용해서 역행렬을 구해보자.
먼저, 이를 위해서는 Determinant에 대해서 조금 더 알아보아야 한다.
Determinant를 구하는 방법은 다음과 같았다.
=> 각 행과 각 열에서 안 겹치도록 하나씩 골라서 다 곱해준 것을
=> "부호"를 고려해서 더할지 뺄지 생각하면 된다.
이 때, Permutation을 다음과 같은 방법으로 잡아보자.

그러면, det A를 계산할 때, 각 성분을 빼서 이런 식으로 생각해볼 수 있다!
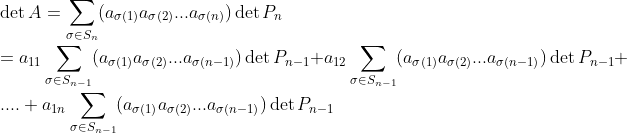
(여기서 a_sigma(1)....은 각 Permutation에 대응되는 A의 성분이고, P_n은 (n by n) Permutation matrix를 말한다.)
즉, 저 a_11 옆에 있는 sum은 위에서 a_11을 잡았을 때 나오는 파란 색 행렬(Submatrix)의 Determinant와 비슷하게 된다!
(같지는 않다! => 왜냐하면 부호를 고려해주어야 하기 때문!)
이 값을 우리가 Cofactor라고 하고, a_ij와 대응되는 Cofactor를 C_ij라고 한다.
그러면 우리는 다음과 같은 식을 얻을 수 있다.
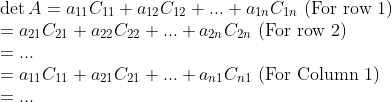
이 때, Cofactor는 다음과 같이 생각하면 된다. (부호 고려!)

=> 이러한 방식으로 생각한다면
=> 크기가 큰 행렬의 Determinant를 계산할 때, 작은 것의 Determinant의 Sum으로 계산할 수 있다는 것을 알 수 있다!
(물론, 크기가 크면 계산도 쉽지 않다! => 연산이 기하급수적으로 늘어남)
계산이 어렵다는 단점이 있지만, 이를 이용하면 역행렬 공식을 아주 심플하게 뽑아낼 수 있다!!!
한번 다음과 같은 연산을 살펴보자!
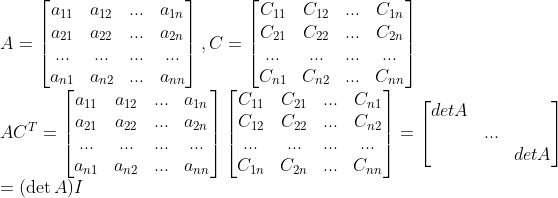
AC^T를 계산할 때, 대각성분이 아닌 경우 잠시 생각해보면...

결국 Cofactor에 해당되는게 오른쪽 행렬의 빨간부분을 제외한 부분에서 위처럼 고르는거기 때문에,
같은 열이 있으므로, 값은 0이 되어야 한다.
어쨌든 간에, 위 식을 이용하면 다음 역행렬 공식을 얻을 수 있다!!

=> 아주 심플하게 역행렬을 계산하는 방법은 얻었지만
=> Cofactor의 Matrix를 다 구해야 하는데, 이게 위에서 보았듯이 만만치 않다!!!
구한 역행렬 공식을 이용해서 Cramer's Rule을 잠시 살펴보자.
Cramer's Rule은 정사각행렬 A에 대해서 다음 x를 바로 수식적으로 구해준다.

(Cramer's Rule)

(즉, B_j는 A에서 j번째 column을 b로 바꿔치기한 것이다!)
어차피 A가 Invertible이 아니면, x 값은 존재할 수 없고,
A가 Invertible인 경우, 위의 역행렬 공식을 이용하면 금방 위의 내용을 증명할 수 있다!

이 Cramer's Rule을 보면 재밌는 사실을 알 수 있는데,
위에서 x가 Determinant의 비율로 나온다는 것이다...
=> 저 A를 "좌표계 변환"이라는 관점으로 생각한다면... => ((x가 이루는 Space) -> (b가 이루는 Space))
=> A에 의해서 "저 Space의 부피(Volume)가" determinant의 비율로 바뀐다!
=> Determinant of Jacobian!!!
ex) 3차원 직교 좌표계 -> 구 좌표계로 옮기는 경우!

여기까지 Determinant에 대한 기본적인 내용을 살펴보았다.
다음 시간에는, (예상외로 잘 쓰이는.... ) Block Matrix에서 Determinant가 어떻게 되는지 살펴본다.
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) Summary 1. Ax=b를 어떻게 푸는가? (1) | 2023.07.16 |
|---|---|
| (선형대수학) 10-3. Block Matrices -> Block Determinants (0) | 2023.07.14 |
| (선형대수학) 10-1. Introduction of Determinants (0) | 2023.07.13 |
| (선형대수학) 9-부록. Fast Fourier Transformation (1) | 2023.07.12 |
| (선형대수학) 9-2. Gram-Schmidt 방법 (0) | 2023.07.11 |



