이번 챕터에서는 행렬식(Determinants)이다!!!
먼저, 행렬식의 정의에 앞서서 어디에 사용이 되는지 잠시 살펴보자.
이미 행렬식에 대한 내용은 다들 들어보았을텐데, 가장 심플하게 알려져 있는 것이
=> 역행렬을 구할 때 나오는 "분모" 일 것이다.

=> 이러한 내용을 넘어서서 행렬식이 어디서 또 나오는지 살펴보자.
1. 역행렬의 존재조건!

=> 2 by 2 행렬의 경우는 위에서 소개한 것과 동일하다!
=> n by n 행렬로 일반화되었을 경우에도 동일할까??
2. 역행렬을 구하는 공식!

=> 2 by 2 행렬의 경우는 위에서 소개한 것과 동일하다!
=> n by n 행렬로 일반화되었을 경우에는 역행렬 공식이 어떻게 될까?? (Cramer's Rule)
3. 미적분학(미적분학 카테고리 참고)

=> 다변수함수의 적분(미적분학 카테고리 참고)에서 보았듯이 Jacobian의 행렬식은 미소부피의 변화량을 말한다!
4. LDU Decomposition => Pivot!

(2-2 내용 수정되었습니다! => P: Permutation Matrix)
=> Gauss-Jordan Matrix에서 도출되는 내용!
=> Determinant의 성질을 알면 금방 증명 가능!
그러면 지금부터 행렬식(Determinants)의 정의를 살펴보고, 위에 내용에 어떻게 적용이 되는지 살펴보자!
당연히 n by n => 정사각행렬에서만 정의된다!
(Determinants)
Notation은 다음과 같다.

1. Permutation Matrix의 Determinants
(NOTE) Permutation은 각 행과 각 열에 1이 1개밖에 존재하지 않는다!
=> 이 행렬의 행(혹은 열)을 자리바꿈을 통해서 Identity Matrix로 만들 때,
=> 홀수번 자리바꿈 : det P=-1, 짝수번 자리바꿈 : det P=1
ex)

2. General Case

=> 위와 같은 행렬이 주어졌을 때, A의 모든 permutation을 잡아버리자!
=> 그리고 그 Permutation의 Determinant와 거기에 해당되는 원소를 다 곱한 후 더하면 Determinant가 된다!

(여기서 sgn(sigma)를 그냥 위의 Permutation의 determinant라고 생각하면 된다.)
ex)

정의가 복잡해보이지만
=> 각 행과 각 열에서 안 겹치도록 하나씩 골라서 다 곱해준 것을
=> "부호"를 고려해서 더할지 뺄지 생각하면 된다.
3 by 3 정도까지는 이 정의를 이용해서 손으로 계산해서 Determinants를 구할 수도 있지만, 더 큰 행렬의 경우 상당히 골치 아파진다...
이를 해결하기 위해서 Determinants의 성질들을 먼저 살펴본 후 조금 더 HARD한 경우로 넘어가보자.
(Properties of Determinants)
1. Identity Matrix의 Determinants는 1

1-1. Diagonal Matrix의 Determinants

위의 내용은 아주 간단하므로 따로 증명은 안한다.
2. Row(Column) Exchange를 한 번 할 때마다 => Determinant의 부호가 바뀐다!
ex)

왜 이런지 생각해보면, General Case 정의에서 Permutation을 잡을 때,
저렇게 한번 Row나 Column이 서로 자리를 바꾸면,
바뀐 행렬에서 Permutation을 잡을 때도 자리가 바꾼채로 잡으면 되고,
이 때, Permutation을 Identity Matrix로 만들 때에도 자리가 바뀌었기 때문에 한번 더 자리를 바꾸어야 한다.
=> 그러므로 모든 permutation이 1번 더 자리 바꾸어야함 => 부호가 다 바뀜! (짝수 <-> 홀수)
3. Determinants는 Row-wise(혹은 Column-wise) Linear operation이다!
3-1. Row/Column Addition

ex) 2 by 2

3-2. Multiplication to Row/Column

3-2-1.

(NOTE)
여기서 헷갈리지 말아야 할 것은 각각의 Row / Column에 대해서 생각해야하고,
3-2-1처럼 전체적(즉, n개의 행/열에 변화)으로 더해지거나 곱해지면 n번 연산해야 한다!
(증명)
3-1. Row Addition
General Case의 정의로 행렬식을 구해본다고 하자.
그러면 Permutation을 잡아서 성분과 곱한다고 했을 때...
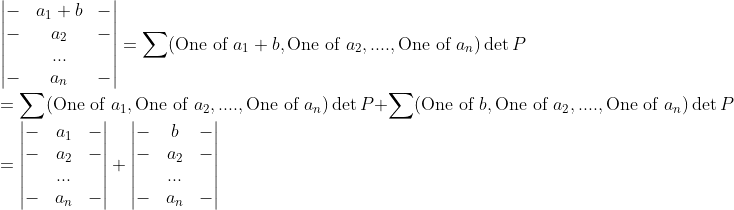
즉, a_1과 b를 쪼개버릴 수 있다.
3-2. Multiplication
이 경우도 General Case를 생각하면 a_1의 성분을 고를 때 c배 증가한 것으로 골라지므로 determinants도 c배 증가한다!
4. Zero Row/Column이 존재하면 det A=0
=> 각 행과 각 열에서 안 겹치도록 하나씩 고르면 0이 한번은 등장하므로 곱하면 모두 0이 된다!
5. 같은 Row/Column이 존재하면 det A=0
=> 2번을 이용하면 증명할 수 있다!

6. 자신이 가지고 있는 Row/Column으로 행연산/열연산 하면 Determinant는 그대로!
=> Gauss-Jordan에서 했던 열/행에 대한 연산을 해주어도 Determinant는 그대로!
=> 5번과 결합하면, 결국 Linearly Dependent한 Row/Column이라면 det A=0이다!!
=> 역행렬의 존재조건!
ex)

(증명)
위의 5번을 이용하면 된다!
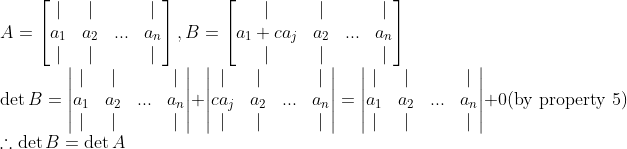
7. Triangular Matrix의 Determinants => 대각성분의 곱!

=> 예상외로 유용하게 써먹는다!
=> 증명은 Gauss-Jordan Elimination에서 Back-Substitution으로 해를 구하는 것을 생각하면 된다.
=> U를 Diagonal Matrix로 고칠 때, 6번에서의 과정만 거치면 되므로, 결국 Diagonal Matrix와 동일해진다!

8. Product Rule

=> 상당히 중요하고 잘 써먹는 공식이다!
=> 더 나아가서 LDU Decomposition에서 다음과 같이 생각할 수도 있다.

(L, U는 대각성분이 모두 1, 그리고 P의 경우 determinant=1 or -1이다!)
(증명)

이 때, 아무 n by n matrix A를 끌고 오자. 그러면, A는 Gauss-Jordan Elimination을 통해서 Upper Triangular Matrix로 만들 수 있고, 이를 다시 Diagonal Matrix로 만들 수 있다. 이 때, Determinant가 바뀌지 않는다! (by 6)
그러므로, 저 D 대신에 A로 치환할 수 있다!
=>

8-1. Determinants for Inverse Matrix
=> 위의 내용을 이용하면 다음과 같은 식을 얻는다!

9. Transpose

=> Transpose를 하면, 결국 Permutation에서 Identity를 만들 때, 행을 기준으로 하는지 / 열을 기준으로 하는지만 바꿔서 생각하면 된다!
=> 그런데, determinant의 정의에서 행을 기준으로 해도 되고, 열을 기준으로 해도 동일하므로, 결국 Transpose에 의한 Determinant의 변화는 없다!
여기까지 Determinant의 성질들을 살펴보았고, 다음 시간에는 더 큰 크기의 행렬식을 어떻게 구할지, 그리고 역행렬 공식은 어떻게 끄집어 낼지 알아보자!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 10-3. Block Matrices -> Block Determinants (0) | 2023.07.14 |
|---|---|
| (선형대수학) 10-2. 역행렬 공식 by Determinant (0) | 2023.07.14 |
| (선형대수학) 9-부록. Fast Fourier Transformation (1) | 2023.07.12 |
| (선형대수학) 9-2. Gram-Schmidt 방법 (0) | 2023.07.11 |
| (선형대수학) 9-1. Orthogonal Matrix (1) | 2023.07.11 |



