앞 챕터에서 Fast Fourier Transformation에 대한 내용이 나왔으므로, Fast Fourier Transformation에 대해서 잠깐 알아보고 넘어가려고 한다.
(Fourier Series를 모르면 그냥 넘어가자!)
먼저, Fourier Series의 Coefficient를 구하는 것부터 시작해보자.
(Fourier Coefficient)

푸리에 급수의 Coefficient를 구하는 것은 해석학 파트에서도 설명이 되어 있으니, 자세한 설명은 해석학 파트를 참고!
이 때, f(t)가 주어진 Interval 안에 주어져 있어야 하는데
이를 조금 확장해서 실수 전범위로 넓혀보자. 그리고, exp의 주기성을 고려해서, int -> 2pi의 상수배로 바꾸자!
=> Fourier Transformation!!
((Continuous) Fourier Transformation)

이를 푸리에 변환이라고 하는데, 푸리에 급수의 의미를 그대로 가져올 수 있으므로 주어진 함수 f(t)를
=> Time-Domain -> Frequency-Domain
으로 변환하는 의미를 가지고 있다.
사실, Laplace Transformation의 상위버전이라고 생각해도 되는게, Fourier Transformation에서는 "허수"파트를 Explicit하게(i가 보이게) 집어넣어주었다!
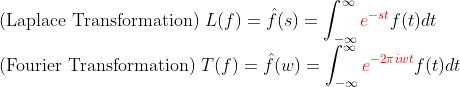
즉, Kernel의 생김새만 약간 다를 뿐, 동일한 표현이다!!
(다만, s에는 복소수(실수+허수), w에는 실수가 들어가는게 일반적!)
그러므로, Laplace Transformation에서 했던 내용 그대로 Fourier Transformation에 적용될 수 있다!
=> 미분방정식 풀 때 유용한 것도 그대로!
위의 Fourier Transformation을 계산하면 복소수가 튀어나올 가능성이 있으므로 => 실수파트와 허수파트를 나누고 싶다!!!
이렇게 나온 것이 Fourier Cosine/Sine Transformation이다.
실수부분과 허수부분을 쪼갤 때는 오일러 공식을 이용하면 심플하다.

(Fourier Cosine/Sine Transformation)
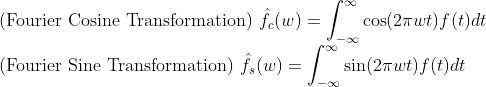
cos이 Even function, sin이 Odd Function이라는 점을 이용하면, 계산이 조금 더 편해지는 장점이 있다.
그리고, 원래의 Fourier Transformation과의 관계를 살펴보면...

여기까지 심플하게 푸리에 변환에 대한 이야기를 해보았다.
위에 나온 푸리에 변환을 수치적으로 계산한다고 생각해보자.
일단 가장 문제되는 포인트가 "특이적분"일 것이다. 이를 해결하기 위해서
적분을 => 무한합으로 고치자!
게다가 무한대까지 적분하는 것이므로, 그냥 각 구간의 길이를 1로 잡자!
그리고, 저 연속함수의 값이 모든 영역에서 필요한 것은 아니다...
-> 구간 별로 함숫값만 알면 된다! -> 각 구간에서 사용할 값들만 sampling하면 된다!!
이렇게 되면 각 구간마다 f(t)는 상수! -> f(n)!
(Discrete-Time Fourier Transformation (DTFT))

여기서 잠깐 생각할 것은 f(n)을 함수가 아닌 수열로 놓아도 된다는 것이다.
그래서 일반적으로 f(n)보다는 x[n]으로 표현한다.

또한, 각 구간의 길이를 1로 놓았었던 것을 확장시킬 수도 있다. (즉, 1초마다 측정하지 않아도 된다.)
=> 각 구간의 길이를 T라고 한다면 (T초마다 측정 -> Sampling Time = T (sec))
=> 이 때, 샘플링 주파수는 1/T=f (1/sec) 가 된다.
=> 각속도와의 관계도 아래에서 살펴보자!

(NOTE)
(푸리에 변환) ~ (라플라스 변환)과의 관계와 비교해보면...
=> (DTFT) ~ (z-transformation(z-변환))과 대응이 된다!
그런데...
x[n]을 측정하는 입장에서 우리가 x[n]을 다 알 수는 없기 때문에 (n이 아주 큰 경우는 아주 오랜시간이 걸릴 것임!!)
저 무한 합을 "일정 길이로 끊어버린다!"
이렇게 "Finite 길이의 수열"로 푸리에 변환을 하는 것을 Discrete Fourier Transformation(DFT)라고 한다!
(Discrete Fourier Transformation(DFT))

위의 내용을 생각해보면...
=> x를 주기 N을 가지고 했다고 생각할 수 있다!
=> 또한, frequency를 k/N으로 보았다고 생각할 수 있다!
이를 빠르게 계산하는 알고리즘이 바로 Fast Fourier Transformation(FFT)이라고 생각하면 된다!
저 DFT를 그냥 심플하게 계산한다고 하면 계산 시간이 (N^2)의 Order를 가질 것이다.
그러나, 저 "복소수항 => Roots of Unity(x^n=1 => 근 x를 뜻함)"을 이용하면 계산 시간이 (N log N)의 Order로 줄어들게 된다.
먼저, 잠시 알아두어야 할 내용들을 정리했다.
1. 위에서 보았던 모든 종류의 푸리에 변환이 "선형성(Linearity)"을 만족하므로,
=> 푸리에 변환은 "행렬로 표현 가능!"
2. DFT의 경우 다음처럼 표현 가능하다!

여기서의 F를 Fourier Matrix라고 한다.
=> 그러므로 우리가 요구하는 것은 저 F의 역행렬을 구하는 것이다!
3. 다음과 같은 성질을 알 수 있다!

(w의 의미를 이용해서, 켤레수로 직접 계산해보면 나온다!)
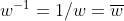
그러므로, F의 역행렬을 바로 계산해버릴 수 있다!

=> 그러므로 우리는 F만 알면 된다!
FFT에는 여러 알고리즘이 있지만, 여기서 소개할 것은 다음 알고리즘이다.
"Cooley-Tukey Algorithm" => 전형적인 Dynamic Programming
먼저, Notation을 살펴보자.

(Background)
위의 Notation을 생각해본다면 다음과 같은 사실을 쉽게 알 수 있을 것이다.

그렇다면, 이를 이용해서 => 문제를 "반으로 줄여버릴 수 있지 않을까?"
(Cooley-Tukey Algorithm)
!짝수항과 홀수항을 나누어서 생각해보자!
즉, X'={X[0],X[2],....}, X''={X[1],X[3],X[5],....}로 나누어서 생각해보자.
X', X'' 각각 항의 개수가 N -> N/2로 줄어든다.
그러면, 위에서 생각해본 다음과 같은 식

을 X', X''에서 그대로 사용할 수 있다!
식으로 써보자면

그러므로, 다시 Recursive하게 빨간부분, 파란부분을 계산하면 된다! (2차원 행렬이므로 적어도 1/4 Easily)
게다가 나머지 k=N/2,N/2+1,...,N-1의 경우에는
=> 켤레수 이용하면 된다!!! => (반바퀴 차이!)
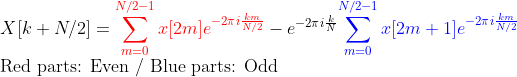
이를 "행렬표현"으로 옮겨보자!
1. 짝수항과 홀수항 분리
=> Permutation Matrix 필요
2. "반으로 나뉜 부분의 Fourier 연산"
=> 짝수항, 홀수항 => Fourier 연산
3. 다시 Reconstruct!
=> 위에서 본 식을 이용한다면 다음과 같이 Reconstruct가 가능하다. (단지 켤레수만 바뀌었다!)

예를 들어서 N=4인 경우를 살펴보자...





이런식으로 Recursive하게 Fourier Matrix를 구할 수 있다는 것이 바로 "Cooley-Tukey Algorithm"이다!
'Mathematics > 선형대수학' 카테고리의 다른 글
| (선형대수학) 10-2. 역행렬 공식 by Determinant (0) | 2023.07.14 |
|---|---|
| (선형대수학) 10-1. Introduction of Determinants (0) | 2023.07.13 |
| (선형대수학) 9-2. Gram-Schmidt 방법 (0) | 2023.07.11 |
| (선형대수학) 9-1. Orthogonal Matrix (1) | 2023.07.11 |
| (선형대수학) 8-2. Weighted Least Squares (0) | 2023.07.11 |



