이번 챕터에서는 앞에서 언급한 대로 Wronskian이라는 것을 소개하려고 한다.
먼저, 6-1에서 2차 선형 상미분방정식에서 => 적분상수 2개가 나온다! => 이를 결정하기 위해선 => 서로 다른 조건 2개가 필요하다!! -> 이 때 초깃값은 y(0), y'(0)으로 잡는것이 일반적이다!!
그런데, 미분방정식 자체가 물리학에서 나온 문제들이 많기 때문에, 결국 이 조건들은 대부분 "초깃값"으로 잡게 된다.
(예를 들어서 F=ma를 통해 물체의 t초 후 위치를 알려고 한다면, 일단은 물체의 초기 위치정도는 알고 있어야 할 것이다!(물론 초기 속도도 알아야 한다))
=> 이러한 문제들을 Initial Value Problem(IVP)(초깃값 문제)라고 한다!
(Initial Value Problem)

(물론 초기시간을 무엇으로 잡느냐에 따라 t=0일 수도, t=t0일 수도 있을 것이다.)
(NOTE)
이와 비슷한 예로 Boundary Value Problem(BVP)(경곗값 문제)도 존재하는데, 6-1에서 보았던 y(0), y(ln 4)를 조건으로 준 문제를 생각하면 된다.
(예를 들어서, 양 끝이 고정된 기타 줄의 변위 y(Position)를 시간에 대한 함수로 표현할 때, 기타 줄 양 끝의 위치를 x=0, x=L이라고 한다면, y(0)=0, y(L)=0 (모든 시간에 대해서) 이어야 한다. 물론 편미분방정식으로 가서 더 자세히 설명한다.)
그런데, 초깃값 문제에서 서로 다른 초깃값 조건 2개가 있어야 2개의 변수를 정할 수 있을 것이다! (마치, 선형연립방정식에서 평행하면 해가 딱 떨어지지 않는다는 것을 생각하면 된다! => 선형대수학 참고!)
이 때, 서로 다른 조건이라는 것은 선형대수학 관점에서 본다면
(평행하지 않는다! => 역행렬이 존재한다! => 서로 선형독립) 이라는 것을 뜻할 것이다.
이를 2차 선형미분방정식에서 생각해보자.
계수가 모두 상수인 경우 일반해는 다음과 같이 나오는 것을 확인했었다.

이 때, 초깃값 문제를 생각해서 c_1,c_2를 결정해보면...
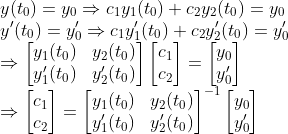
결국 저 역행렬의 존재 여부에 따라서 c_1과 c_2가 결정나는지 아닌지 알 수 있을 것이다. 게다가
역행렬이 존재하지 않으면 => Determinant(행렬식) = 0이므로 결국 이 Determinant를 아는 것이 아주 중요하다.
그러므로, 우리는 저 Determinant를 Wronskian이라고 정의한다.
(Wronskian)

(확장해서 t_0에서만의 값이 아니라 t에 대한 함수로 생각하자.)
2차 선형미분방정식 말고도, 고차로 넘어가도 상관은 없다.
느낌이 올수도 있지만, 고차로 넘어가도 일반해는 다음처럼 표현이 되고,
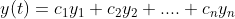
그러면 Wronskian도 다음과 같이 정의하면 된다.

정리하면 저 초깃값(t=t_0)에서 Wronskian=0이 되면 Initial Value Problem의 해를 구할 수가 없다!!!
(Example)
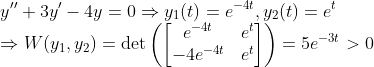
Wronskian이 언제나 0보다 크므로, 초기 시간을 어디로 잡든간에 초깃값 문제를 풀 수 있다!(c_1,c_2를 결정할 수 있다.)
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 7-1. 2nd-Order ODE with Constant Coefficients (1) (1) | 2023.12.28 |
|---|---|
| (미분방정식) 6-3. General Solution of 2nd-order ODE (1) | 2023.12.16 |
| (미분방정식) 6-1. 2nd-Order ODE (1) (0) | 2023.12.16 |
| (미분방정식) 5. Stability in 1st-ODE (1) | 2023.11.19 |
| (미분방정식) 4. Application of 1st-ODE (0) | 2023.11.12 |



