이번시간에는 2차 선형 상미분방정식을 살펴보자.
사실, 1차 미분방정식보다는 훨씬 더 많이 보이는데, 아무래도 물리학의 기본이 되는 "F=ma"가 바로 2차 미분방정식이기때문이다. (x가 시간 t에만 관여된 함수이면, 편미분이나 상미분이나 똑같다!)
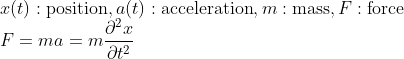
그러면 2차 상미분방정식의 일반적인 형태를 살펴보자.
(2nd Ordinary Differential Equation)
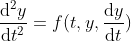
그러면, 앞에서 보았던 것처럼 선형이면 다음처럼 표현할 수 있을 것이다.
(Linear Form)
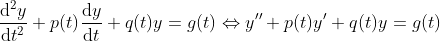
이 때,
(Homogeneous Form)

(Non-Homogeneous Form)
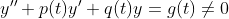
라고 볼 수 있다!
그럼, 일단 쉬운 문제부터 생각해보자! -> p(t), q(t) : 상수인 경우!
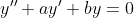
1차 상미분방정식의 경우에는 식을 적분이 가능하도록 억지로 바꾸어서 계산을 했지만, 고차로 올라가면 직관적으로 그런식의 식 변형이 잘 보이진 않는다...
이 문제를 푸는 아이디어는 다음과 같다.
(IDEA)
우리가 잘 아는 함수 중에서, 저 방정식의 해가 되는 것을 고려해보자... 사실, 우리가 아는 함수가 그렇게 많지는 않다.
1. 유한차항 다항함수(Polynomial)
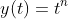
이걸 방정식에 한번 넣어보자...
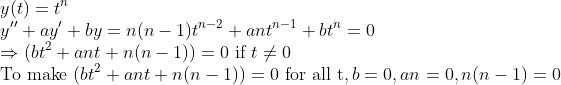
위 다항식이 t에 대한 "항등식"이 되려면 t^2, t, 상수가 모두 0이 되어야 하는데, a,b는 이미 정해진 값이므로, 일반적인 경우에 저 다항식은 0이 되지 않는다!
그러므로 유한차항 다항함수는 "일반적인 2차 상미분방정식"의 해로써는 불합격이다.
2. 삼각함수 -> 일반적으로 Exp함수! (오일러 공식)
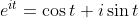
1차 미분방정식을 풀 때에 자주 나오는 Exponential 함수를 사용해보자...
게다가 Exponential 함수는 복소수범위로 넘어가면 삼각함수도 포함하고, 미분을 하면

위와 같이 나오므로, 미분을 해도 새로운 함수가 튀어나오지 않기에 식 정리에도 용이해보인다.
그러면, 다음처럼 exponential함수를 2차 상미분방정식에 넣어보자!

이 때, 저 빨간 식을 Characteristic Equation(특성방정식)이라고 부른다!
즉, 정리하면 특성방정식의 해를 구해서 나온 lambda를 y(t)에 집어넣으면 바로 해가 된다!!
(Example)

그런데, 선형방정식의 특성상 이 해들의 선형결합도 해가 된다! (1. Classification of Differential Equation 참고)
즉, 다음 식이 위 미분방정식의 "일반해"가 된다.
(Principle of Superposition(중첩원리))
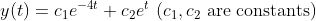
이게 해가 되는 것을 확인해보자.
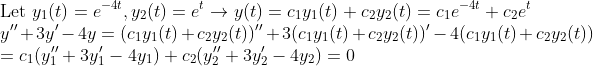
이렇게 y=c_1y_1+c_2y_2일 때, (y에 관한 식) -> c_1(y_1에 관한 식) + c_2(y_2에 관한 식)으로 쪼개지는 것은 바로 이 미분방정식이 "선형(Linear Form)"이기 때문이다!!
또한, 이 때의 c_1, c_2는 앞의 1차 미분방정식과 비교해보면 => 적분상수라고 생각할 수 있다!!!
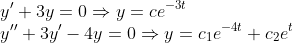
그러므로, 초깃값이나 다른 조건들에 의해서 c_1,c_2는 결정된다!
그런데, y에 대한 초깃값을 생각해보면, y(0)=y_0 1개가 나오는데, 2개의 변수를 어떻게 결정할까?
=> 이 경우에는 1개의 조건이 더 필요하다!
=> 가장 만만한 경우가 y'(0)을 결정해주는 경우이다!
(Example)
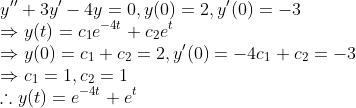
물론, y'(0) 말고 Boundary Condition처럼 결정해줄 수도 있다.
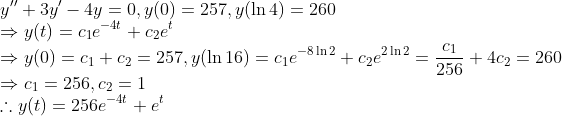
즉, 적분상수가 2개이니, 결국 2개의 서로 다른 조건이 필요하다는 것만 염두해두면 된다!
=> 예를 들어서, 더 나아가면 5차 상미분방정식이 된다면 5개의 조건이 필요할 것이다!
여기까지 2차 상미분방정식을 어떻게 푸는지 살펴보았는데, 1차 상미분방정식에서 본 것 같이, 우리가 구한 해가 "유일"한지, 아니면 다른 해의 리스트가 더 있는지는 아직 살펴보지 않았다.
일단 여기에 대한 답은 다음으로 미루도록 하고, 다음 시간에는 이론적으로 내용을 전개해나갈 때 중요한 "Wronskian"에 대해서 알아보자!
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 6-3. General Solution of 2nd-order ODE (1) | 2023.12.16 |
|---|---|
| (미분방정식) 6-2. Wronskian! (0) | 2023.12.16 |
| (미분방정식) 5. Stability in 1st-ODE (1) | 2023.11.19 |
| (미분방정식) 4. Application of 1st-ODE (0) | 2023.11.12 |
| (미분방정식) 3-3. Existence & Uniqueness of Solution of 1st-ODE (3) (1) | 2023.11.12 |



