6-1에서 계수가 상수인 2차미분방정식을 어떻게 푸는지 간단하게 보았는데, 이번 챕터에서는 조금 더 자세히 알아보도록 하자.
먼저, 계수가 상수인 2차미분방정식을 어떻게 풀었냐면
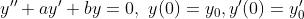
=> 특성방정식(2차방정식)을 풀고
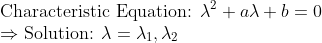
=> 해를 다음과 같은 형식으로 놓고
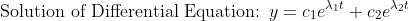
=> 초깃값을 집어넣어서 해를 구한다!
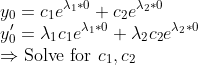
그러면 c1,c2를 구할 수 있으니 그대로 해를 써주면 그게 바로 2차미분방정식의 해였다!!
이 때, 우리는 특성방정식의 해의 종류를 기준으로 조금 더 알아보려고 한다.
=> 실근 2개 (7-1에서 설명)
=> 중근 1개 (7-3에서 설명)
=> 허근 2개(켤레복소수) (7-2에서 설명)
먼저, 실근이 2개인 경우 나올 수 있는 케이스는 다음과 같다.
=> 양수 2개
=> 양수 + 음수
=> 음수 2개
(해가 0인 경우는 일단 제외)
(1) 양수 2개
예시를 통해 알아보자.
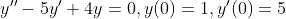
풀어보자!
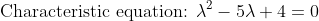
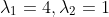
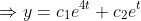
그러므로 초깃값을 넣어서 계산해보면
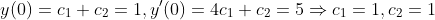
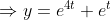
이 경우에는 e^(4t), e^(t) 때문에
시간이 가면 갈수록 해가 "발산"하는 경향성을 보인다! (e^(4t)가 결국엔 Dominant하게 해를 지배한다.)
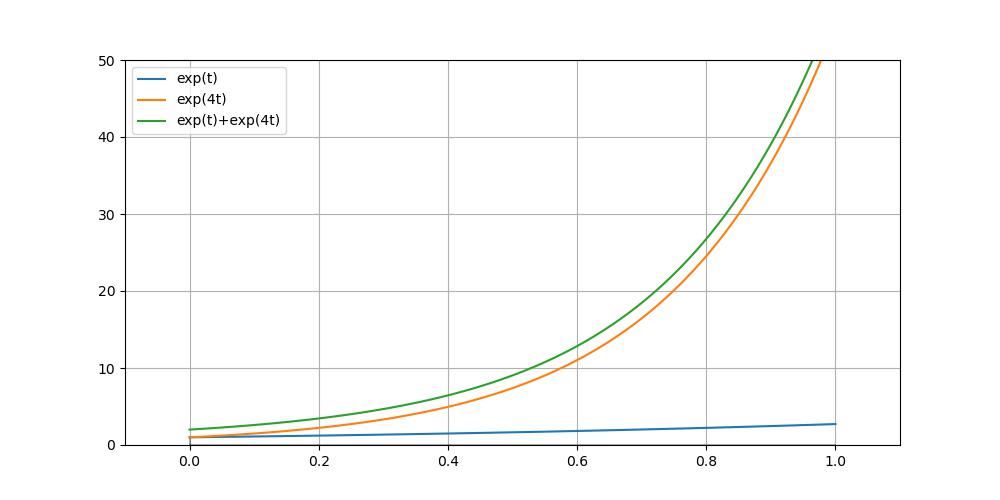
(2) 양수 1개 + 음수 1개
예시를 통해 알아보자.
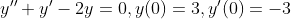
풀어보자!
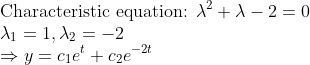
그러므로 초깃값을 넣어서 계산해보면
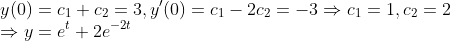
이 경우에는 다음과 같으므로
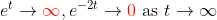
e^t 하나 때문에 시간이 가면 갈수록 해가 "발산"하는 경향성을 보인다! (e^(t)가 결국엔 Dominant하게 해를 지배한다.)
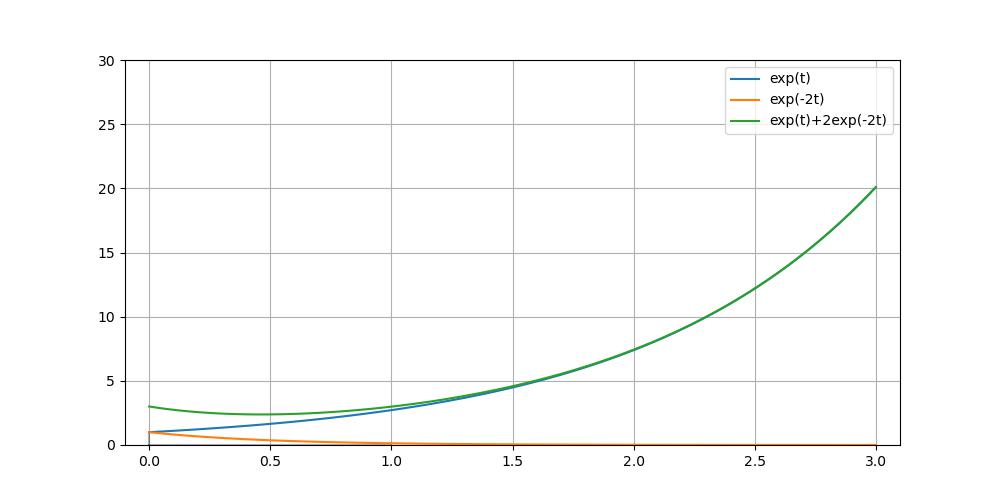
(3) 음수 2개
예시를 통해 알아보자.
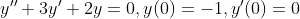
풀어보자!
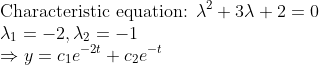
그러므로 초깃값을 넣어서 계산해보면
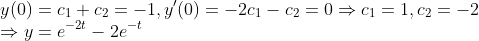
이 경우에는 다음과 같으므로
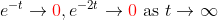
시간이 가면 갈수록 해가 "수렴"하는 경향성을 보인다!
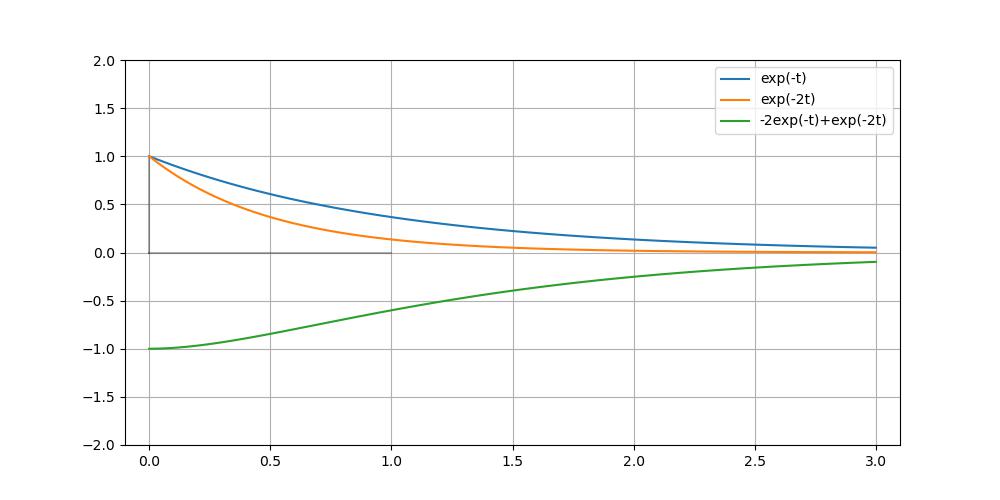
=> 즉, "특성방정식의 해가 모두 음수여야 해는 수렴한다!!!!"
물론, t가 마이너스 무한대로 가면 이와 반대의 현상이 발생할 것이다. 그러나, 미분방정식이 쓰이는 곳이 대부분 "물리학"이고, 시간에 대한 미분으로 시스템을 모델링하기 때문에, 마이너스 시간이 있지 않은 한, 대부분의 경우에는 "양의 무한대"로 시간이 흘러가는 것이 중요하다.
또한, 해가 발산한다는 것은 결국 "물리량"이 발산한다는 말이므로, 시스템에 좋지 않은 영향을 줄 것이 자명하다. 그렇기 때문에 앞에서 보았던 해의 "안정성"과도 관련이 된다.
=> "특성방정식의 해의 부호는 시스템의 안정성과 관련이 있다!!!!"
=> "특성방정식의 해가 모두 음수여야 시스템이 안정하다!!!!"
심플하지만, 아주 중요한 이야기이므로 꼭 기억하자!
(NOTE)
특성방정식의 해가 0이 나온다면?
그렇다면, 특성방정식의 상수항은 0이라는 말이 되므로, 미분방정식의 꼴은 다음과 같이 나온다.
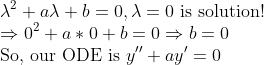
그러면, y'=z로 놓으면 그냥 1차미분방정식이 되므로, 1차미분방정식으로 생각하면 된다.
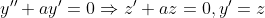
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 7-3. 2nd-Order ODE with Constant Coefficients (3) (1) | 2024.01.06 |
|---|---|
| (미분방정식) 7-2. 2nd-order ODE with Constant coefficients (2) (1) | 2024.01.06 |
| (미분방정식) 6-3. General Solution of 2nd-order ODE (1) | 2023.12.16 |
| (미분방정식) 6-2. Wronskian! (0) | 2023.12.16 |
| (미분방정식) 6-1. 2nd-Order ODE (1) (0) | 2023.12.16 |



