(NOTE)
이번 시간에는 적어도 연속함수, 미분, Topology에 대한 기본적인 해석학 지식이 필요합니다!!! -> 해석학 카테고리 참고!
이번 시간에는 1차 비선형 상미분방정식의 해의 존재성과 유일성에 대해서 알아보자.
그 전에, 미분방정식의 해를 어떻게 표현할지부터 더 생각해야 한다.
(Explicit Form)
미분방정식말고, 흔히 그냥 함수를 표현할 때 이런 식으로 표현할 것이다.
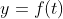
ex)
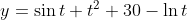
이런 식으로 y를 (y에 대한 변수 t)에 대한 항으로만 써줄 수 있으면 Explicit Form이라고 한다. (아래의 Implicit Form과 비교해보면 바로 느낌이 온다.)
(Implicit Form)
Explicit Form처럼 표현하지 않고, 그냥 한쪽으로 다 몰아서 쓴 형식을 Implicit Form이라고 한다. 즉, 다음 표현을 말한다.

ex)

tan 함수와 exponential 함수들이 섞여있어서, y만 떨어뜨리기가 사실상 불가능하다....
=> 둘을 비교해보면 알겠지만, Implicit Form이 Explicit Form보다 더 일반적인 표현이다! (그냥 한쪽으로 몰면 된다!)
자, 그러면 다시 미분방정식으로 돌아오자.
그러면, 1차 비선형 상미분방정식을 어떻게 쓸지 생각해보자.
=> 가장 폭 넓게 생각해보면 다음처럼 Implicit Form을 이용하면 될 것이다.
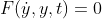
그런데, 이 경우는 정말로... 문제가 복잡해지므로, 적어도 Explicit Form까지는 양보하자... (사실, 공부할 때 위처럼 미분방정식을 쓸 일이 없다.)
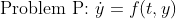
이 때, f는 t와 y에 대한 다변수함수가 될 것이다!
그리고, 선형상미분방정식에서 본 것같이 적분상수를 결정하기 위해서, Initial Condition 한 개를 추가하자.
-> 아래 나온 식이 해의 존재성과 유일성을 다룰 우리의 1차 비선형 상미분방정식 꼴이다. (물론, t와 y가 적절한 범위에서 정의되어 있다고 하자.)

그리고, t_0, y_0을 어떤 값으로 놓는다고 해도, 해의 존재성과 유일성을 증명할 때, 따로 문제될 것은 없으므로(그냥 평행이동하면 되는 문제!) t_0=0, y_0=0으로 놓자!
이 때, 우리의 해 phi(t)는 다음처럼 "적분" 꼴로 놓을 수 있다...
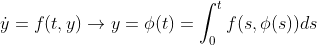
사실 별 건 없고, 그냥 원래 문제에서 y를 phi(t)로 넣고, t에 대해서 적분했을 뿐이다....
(해의 형태를 저렇게 쓸 수는 있지만, 저 식이 진짜로 존재하는지는 다른 문제....)
=> 즉,
1. 위 식을 만족하는 phi 함수가 존재하는지? -> "해의 존재성" 문제
2. phi 함수가 존재하는데 하나만 존재하는지? (with Initial Condition) -> "해의 유일성" 문제
정리하자면, 결국 우리의 문제는 다변수함수 f에 의해서 결정되고, 해는 이 f를 적분한 것으로 생각할 수 있다!!
(Problem)
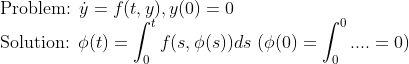
=> 결국, f의 성질에 의해서 해의 존재성/유일성이 결정된다는 사실을 알 수 있다.
=> 게다가, Initial Condition에 의해서 y(0)=0 -> f(0,0)...?
=> f(t,y)의 "원점(0,0)" 근처에서 뭔가 일이 생긴다는 사실을 알 수 있다!
그럼, 언제 해가 "존재"하고 "유일"한지 알아보자.
(Existence & Uniqueness of solutions of 1st nonlinear ODE)

즉, f와 df/dy가 원점(0,0)을 포함한 아주 작은 영역(적분 정의가 깔끔하게 나오기 위해서 Closed set -> Compact set)에서 "연속"이기만 하면, 저 문제의 해가 존재하고, 유일하다!!!!
(증명)
<Method of Succesive approximation (Picard's Iteration Method)>
이 방법을 간단하게 소개하면, 초기 해를 하나 아무거나 잡고, 해를 약간씩 움직여가면서 저 문제의 해를 구하는 방법이다.
(비선형 Optimization 문제를 푸는 기법 중에 -> Stochastic Gradient Descent(SGD)라는 방법을 알고 있는 사람들도 있을 것이다.(몰라도 된다!) 그런 식으로, 초깃값을 잡고 약간씩 해를 움직여 나가는 방법으로 생각하면 쉽다.)
=> 이 개념은 비선형 최적화 문제에서 아주 중요하므로 개념만이라도 알아두자!
(설명)
먼저, SGD에 대해서 간략하게 설명하고 넘어간다.
최적화 문제란, 주어진 비용함수(Cost Function)을 최대화/최소화하는 문제를 말하는데, 예시 하나를 들어서 생각하자.
(선형대수학 카테고리)
(선형대수학) 부록 2-1. Beginning of Optimization Problem: https://0418cshyun.tistory.com/187) 내용입니다!
ex) 재료 A와 B를 이용해서 제품 1과 2를 만들 수 있다고 하자.
다음은 각각 제품 1, 2 1kg를 만들기 위해서 필요한 재료 A, B의 무게를 나타낸 것이다.
| 재료 A | 재료 B | |
| 제품 1 | 5 | 1 |
| 제품 2 | 1 | 6 |
재료 A의 재고는 100kg, B의 재고는 60kg 남아있다고 하자.
그리고 제품 1을 1kg를 팔면 5만원, 제품 2를 1kg를 팔면 8만원을 벌 수 있다고 하자.
그러면, 가장 수익을 많이 내기 위해서는 각각 제품 1,2를 몇 kg씩 만들면 될까???
여기서 제품 1,2를 판 양(kg)을 각각 x,y라고 하면,
2. 수익 : J=5x+8y (만원) => Cost Function!
3. 조건: 5x+y<=100, x+6y<=60
4. 조건2: x>=0, y>=0
=> 저 J를 최대화하는 조건에 맞는 x,y를 찾고, 그 때의 J를 찾는 것이 우리의 목표!
이 문제를 푸는 방법이야 쉽겠지만, 조금 더 이론적으로 들어가보자.
일단 Cost Function은 결국 x,y에 따라서 바뀌는 값이므로, J를 "다변수함수"라고 생각할 수 있다.
또한, 저 조건1,2는 x,y에 대한 조건 => x,y에 대한 영역(S)
=> 다변수함수 J의 S 안에서 최대/최소를 찾는 문제가 된다.
선형대수학 카테고리에서는 "Boundary"에서 최대/최소를 가진다고 했는데, 이는 여러 조건들이 붙긴 하지만, J가 선형함수이기 때문에 그렇기도 하다.
이를 그림으로 나타내면 다음과 같다.
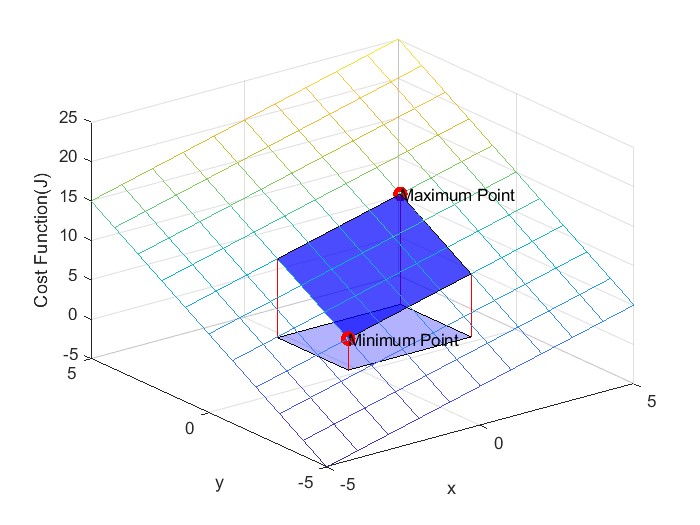
그러면, 이제 J가 위처럼 평면으로 나오는게 아닌, 주식 그래프처럼 아주 복잡하고 진동도 하는 함수(비선형함수)로 되어있다고 하자... 그러면, 당연히 Boundary에서 최대/최소가 나오는 것은 아니라는 것을 직관적으로 알 수 있을 것이다.
이 때, 사용하는 개념이 바로
=> 미분값=0!!! -> 극값을 갖는다!!!
그러나, 극값 자체가 Locally Minimum/Maximum을 말하므로(즉, 전체영역이 아닌 그 주변에서의 최대/최소) 전체의 최대/최소까지는 모르겠으나, 후보들을 추려 내는 정도까지는 가능하다.
그런데, Cost Function가 미분은 가능하지만, 도저히 "전 영역"에서 할 수 없을 정도로 엄청나게 복잡한 함수라면???
(사실, 이런 경우가 허다하다...) 예시를 통해 알아보자.
ex) 테트리스 자동화
테트리스를 자동으로 해주는 컴퓨터 프로그램을 짠다고 하자. (테트리스 블럭이 나오는 순서는 매번 동일하다고 하자.)
우리 블럭은 1초에 1칸만큼 움직일 수 있다고 하자.
그러면,
입력값으로 줄 것 -> 매 시간마다 블럭을 좌우 어디로 어느만큼 움직일지(x(t))
Cost Function(J) -> 테트리스 점수 => 최대화 요구!!!
x(t)를 어떻게 주냐에 따라서 당연히 점수는 바뀔 것이고 -> x의 변화에 따라서 점수는 바뀔 것이다.
=> 그러면, 어떻게 최대 점수를 얻을 수 있는가???
1. x(t)=0으로 준다! (즉, 가만히 있는다.)
2. 이 때 나오는 점수(J0)를 확인한다.
3. x(t)=0에서 한 스텝만 x를 1칸만 바꾼다.
-> 3-1. x(1)=1, x(2)=0, x(3)=0,...... => x1(t) -> 점수 J1
-> 3-2. x(1)=0, x(2)=1, x(3)=0,...... => x2(t) -> 점수 J2
-> .....
4. 이 때 나온 점수 J1,J2,...를 확인하고 가장 점수가 높은 x를 선택한다. (J3이 가장 높다면 x3(t)를 선택)
5. 3->4번을 반복한다! (x(t)=0 대신 x(t)=x3(t)로 놓고 x3에서 또 한스텝씩만 바꾼다!)
=> 계속 반복하면 이 초기위치를 바꾸면서 나올 수 있는 최대 점수가 나올 것이고, 이 때의 x를 구할 수 있다.
(NOTE)
이 때, 미분을 -> x가 변화함에 따라서 점수 J가 변화하는 것! -> 으로 생각한다면, 결국 모든 x에 대해서 J의 미분값을 구하는 것은 말이 안될 것이다... (모든 케이스에 대해서 테트리스를 다 돌려야 하니....)
위의 1-5에서 한 방법이 바로 Locally Maximum/Minimum을 구하는 방법이 된다.
=> 즉, "미분값">0이 되는 지점으로 계속 x를 살살 움직이면서 극값을 찾으면, 적어도 초깃값에서 움직일 수 있는 최댓값을 찾을 수 있다!!
그런데, 이 Locally Maximum/Minimum이 전체 최대/최소가 아닐 수 있다... 왜냐하면 x(t)=0에서 움직일 수 있는 영역은 한정적일 수 있기 때문이다... (즉, 다른 초깃값에서 스타트하면, 더 큰(작은) 값을 얻을 수도 있다.)
그림을 통해서 보면 이해가 빠를 것이다.

초깃값을 어디에 두냐에 따라서 어느 Minimum point로 가는지가 결정되는 것을 볼 수 있다!!!
이렇게 미분값을 통해서 Cost Function이 작은 쪽으로 움직이면서 최소를 찾는 방법을 Gradient Descent라고 한다.
이 때, x를 얼마만큼 움직일지(Step size)는 대부분 Minimum Point로 움직이면서 약간씩 줄여나가는 방법을 사용한다.
(이에 대한 자세한 내용은 최적화 이론 참고! -> 여러 방법들(Euler Method, Adam Optimizer 등등의 방법들이 있다.))
또한, 초깃값을 잡는 문제도 -> 랜덤하게 몇가지 케이스를 돌릴 수도 있고, 중간에 나온 값들을 이용해서 초깃값을 다시 잡을 수도 있고, 여러가지 방법이 있다.
다시 우리의 문제로 돌아와서
<Method of Succesive approximation (Picard's Iteration Method)>에 대하여 설명한다.
우리의 해는 다음과 같이 주어졌다.

그러면, 이 phi(t)를 찾기 위해서 다음과 같은 방법을 쓴다.
1. phi_0(t)(초깃값)을 아무거나 잡는다. (여기선 그냥 0으로 놓자)
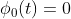
2. 그러면 다음과 같이 순차적으로 phi를 잡아보자.
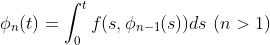
3. 해가 존재한다는 말은 결국 2번 식에서 n과 n-1에서의 phi가 차이가 없어야 한다는 뜻이므로,
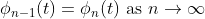
즉 위의 예시 그림과 비교하자면 -> 점(x)이 이동하는 것 대신 함수(phi)가 이동하는 것과 동일하다고 생각하면 된다!
(NOTE)
해석학 카테고리를 참고하면 다음 함수열이 코시수열이라는 말과 동일하다!

간단하게 설명하면, 위의 함수열이 수렴하면 -> 해가 존재한다!!!
(함수열의 수렴과 관련된 내용은 해석학 카테고리 참고!!!)
그러면, 위의 내용대로 한번 해가 존재하는지 살펴보자!
1.


2.
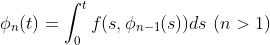
여기서 함수열을 정의하기 위해 모든 n에 대해서 저 phi_n(t)를 정의할 수 있는지, 연속인지 살펴보자.
phi_0(t)가 주어진 t 범위(-a~a)에서 연속이고 잘 정의되어 있으므로, 귀납법을 이용하자. 즉, 다음 사실을 보이면 된다.
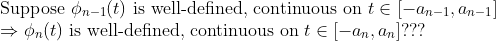
(증명2)
먼저,
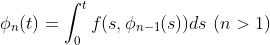
에서 phi_n이 정의가 잘 된다는 것은....
(a-1)
=> 만일, phi_(n-1)(t)가 b보다 크다면, R을 벗어나기 때문에, f의 연속조건에서 벗어나게 된다...
=> 그러므로, phi_n(t)는 언제나 b보다 작거나 같아야 한다!!!
(a-2) f가 R(compact set)에서 연속! => 최댓값과 최솟값이 존재한다!

조금 더 나아가서
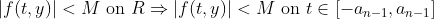
게다가,

인데, 최대최소정리에 의해서 f 값이 bounded 되어있으므로,
=> phi_n(t)의 미분값도 bounded 되어 있다.
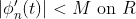
(a-3) 평균값정리에 의해서

그런데 phi_n은 언제나 b보다 작거나 같기를 원했다.
그러므로, c를 다음과 같이 잡는다면...

(증명2 정리)
그러므로 다시 거꾸로 거슬러 올라가서 정리하면...

게다가, f가 연속이고, 구간이 잘 주어져 있으므로, 적분을 해도 연속이다!
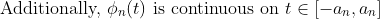
(구간을 n에 대한 수열로 잡았지만, 결국 t가 b/M 안에 있으면 모두 동일하므로, 결국 n에 대한 수열 대신 h로 쓰면 된다.)
3. 이렇게 구한 함수열이 수렴하는지 보아야 한다!!
(사실, 이건 Uniform Convergence와 관련이 있는 내용이므로, 해석학 카테고리를 참고하기를 바란다!)
(증명 3)
여기서는 df/dy의 연속조건을 사용한다.
(3-1) 중간값 정리와, 최대최소정리를 사용한다면 다음 사실을 이끌어 낼 수 있다. (R이 Compact!!!)
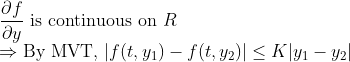
이를 우리가 Lipschitz Condition(립쉬츠 조건)이라고 한다.
사실 Compact set 조건까지는 필요 없고, 이 립쉬츠 조건만 있으면 2번도 증명이 가능하다.
그러므로 다음 사실도 자명하다. (단, t의 범위가 크게 줄어들었다!)

(3-2)
우리가 초깃값을 다음과 같이 잡았다.

그러므로

이를 (3-1)과 합쳐보면...
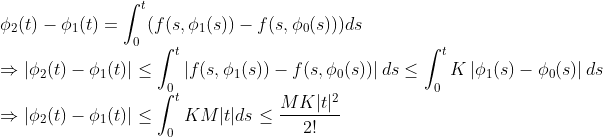

그러므로,
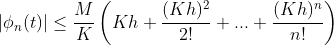

그러므로, 단조수렴정리에 의해서 함수열 phi_n(t)는 수렴하고,
우리가 적어준 해가 존재한다는 것을 증명했다.

해석학 카테고리를 제대로 보고오면 어떤 식으로 증명을 한 것인지 대충 감이 올 것이다.
(물론, 안 보고 오면 상당히 내용이 어려울 것이다.)
아직까지는 해의 존재성만 증명했다. 이제 유일성도 증명해야 한다.....
그러나, 여기까지 쫓아왔다면, 유일성은 쉽다!!!
유일성에 대한 이야기는 다음 시간에 알아보자!
'Mathematics > 미분방정식' 카테고리의 다른 글
| (미분방정식) 4. Application of 1st-ODE (0) | 2023.11.12 |
|---|---|
| (미분방정식) 3-3. Existence & Uniqueness of Solution of 1st-ODE (3) (1) | 2023.11.12 |
| (미분방정식) 3-1. Existence & Uniqueness of solution of 1st-ODE (1) (0) | 2023.11.11 |
| (미분방정식) 2-2. 1st-Order ODE (2) (0) | 2023.11.05 |
| (미분방정식) 2-1. 1st-Order ODE (1) (0) | 2023.11.05 |



